Если членами ряда являются комплексные числа, то ряд примет вид: 
где 
Определение:
Ряд (1) называется сходящимся если сходится по отдельности ряд, составленный из действительных частей данного ряда: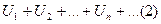 
и ряд составленный из мнимых частей: 
.
Пусть 
то ряд (1) сходится 
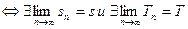
Тогда суммой ряда (1) называется число 
.
Теорема 17.
Если сходится ряд модулей членов ряда (1) то ряд(1) так же сходится.
Доказательство.
- сходится.
(2) сходится по признаку сравнения.
(3) сходится по признаку сравнения при чем абсолютно по определению (1) сходимости.
Степенным рядом в комплексной области называется ряд: 
где 
(4)
По теореме 17(4) сходится если сходится ряд: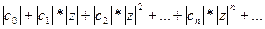 
где 
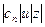- действительные числа=> можно применять все известные признаки.
Пример. Вычислить интеграл 
, где:
а). l - прямая, соединяющая точки z 1 = 0 и z 2 = 1+ i;
б). l - ломаная ОВА, О (0,0), В (1,0), А (1,1).
Решение.
а). Путь интегрирования l - прямая, соединяющая точки z 1 = 0и z 2 = 1+ i.
Применяем к вычислению интеграла 1-й способ (формула (1)). Подинтегральное выражение имеет вид
Re zdz = x (dx + idy) = xdx + ixdy. Поэтому:
Уравнение отрезка прямой, соединяющей точки z 1 = 0и z 2 = 1+ i имеет вид
y = x, 
.
Получаем:
б). Путь интегрирования l - ломаная ОВА, О (0,0), В (1,0), А (1,1).
Так как путь интегрирования состоит из двух отрезков, записываем интеграл в виде суммы двух интегралов:
и каждый из этих двух интегралов вычисляем, как выше.
Для отрезка ОВ имеем: y = 0, ,
а для отрезка ВА: х = 1, 
.
Тогда:
Заметим, что подинтегральная функция в данном примере - функция не аналитическая, поэтому интегралы по двум различным кривым, соединяющим две данные точки, могут иметь различные значения, что и продемонстрировано в этом примере.
Пример.
Вычислить интеграл от аналитической функции
Применяем формулу (3), первообразную находим, используя методы интегрирования действительного анализа:
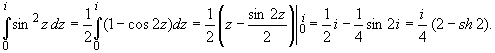
Пример.
Разложить функцию 
в ряд Лорана по степеням z.
Решение. Так как функция является рациональной дробью, то особыми точками являются нули знаменателя, т.е. z 1 = -1 и z 2 = 3. Запишем функцию в виде
Кольца аналитичности | z | < 1, 1 < | z | < 3, | z | > 3.
Раскладываем дробь на элементарные дроби:
При | z | < 1 имеем:
Таким образом, в круге | z | < 1 функция раскладывается в ряд Тейлора:
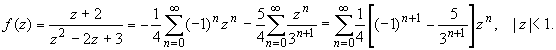
В кольце 1 < | z | < 3:
В итоге имеем: 
В круге | z | > 3:
В итоге имеем: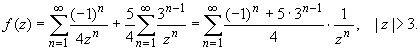 
Пример. Разложить функцию f (z) = z 3· e 1/ z в окрестности точки z 0 = 0.
Решение. Из основного разложения 
получаем
или
Вопросы для подготовки к ЭКЗАМЕНУ
По итогам изучения дисциплины в качестве формы итогового контроля предусмотрен зачет.дготовки
1. Статистическое распределение выборки. Полигон. Гистограмма.
2. Статистические оценки параметров распределения. Точечные оценки математического ожидания, дисперсии, среднего квадратического отклонения, ассиметрии, эксцесса. Метод их вычисления.
3. Метод моментов. Метод наибольшего правдоподобия.
4. Определение вида аналитической зависимости по экспериментальным данным. Метод наименьших квадратов.
5. Интервальные оценки. Доверительные интервалы для параметров случайной величины.
6. Статистическая проверка статистических гипотез (основная и конкурирующая гипотезы, критическая область, статистический критерий, уровень значимости, мощность критерия).
7. Линейная корреляция. Точечная оценка выборочного коэффициента корреляции. Уравнение прямой линии регрессии.
8. Выборочное корреляционное отношение. Метод вычисления.
9. Множественная линейная регрессия. Уравнение прямой линии множественной регрессии.
10. Основная задача дисперсионного анализа.
11. Основная задача однофакторного дисперсионного анализа. Уровни фактора дисперсионного анализа.
12. Нулевая гипотеза и статистический критерий задачи однофакторного дисперсионного анализа. Алгоритм решения задачи однофакторного дисперсионного анализа.
Литература
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах [Текст]: [учеб. Пособие для втузов]: В 2-х ч. Ч.1.-6-е изд. - М.: ОНИКС 21 век, 2012. – 304 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах [Текст]: [учеб. Пособие для втузов]: В 2-х ч. Ч.2.-6-е изд. - М.: ОНИКС 21 век, 2012.– 416 с.
3. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.; Учеб. для вузов инж.-техн. спец. Т. 3: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного; [Под ред. Садовничего В.А.]. ‑ 6-е изд., стер. ‑ М.: Дрофа, 2011. ‑ 511 с. – (Высшее образование: Современный учебник).
Дополнительная
4. Пантина И.В. Вычислительная математика [Электронный ресурс]: учебник/- М.: МФПУ Синергия, 2012. - 176 с. Режим доступа: http://znanium.com/bookread2.php?book=451160
5. Гмурман В.Е. Ттеория вероятностей и математическая статистика: Учеб. Пособие для вузов / В.Е. Гмурман. – 10-е изд., стер. - М.: Высш.шк., 2011. – 404 с.
