Пусть (X;Y) – двумерная генеральная совокупность; n – объем выборки.
rB= 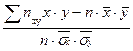 - выборочный коэффициент корреляции.
- выборочный коэффициент корреляции.
В качестве критерия проверки основной гипотезы о равенстве нулю генерального коэффициента корреляции примем случайную величину:
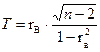 .
.
При справедливости нулевой гипотезы она имеет распределение Стьюдента с 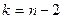 степенями свободы.
степенями свободы.
H0: rГ = 0 - основная гипотеза.
H1: rГ  0 - конкурирующая гипотеза.
0 - конкурирующая гипотеза.
(критическая область – двусторонняя)
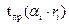
 по таблице Стьюдента для двусторонней области находим критическую точку
по таблице Стьюдента для двусторонней области находим критическую точку 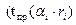
Если 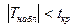 - основная гипотеза
- основная гипотеза  принимается.
принимается.
Если 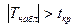 -основная гипотеза
-основная гипотеза  отвергается.
отвергается.
Если H0 отвергается, то X и Y коррелированны (т.е. связаны линейной зависимостью).
Таблица Проверка статистических гипотез
H0: 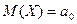 1)
1) 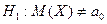 2)
2) 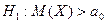 3)
3) 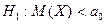 (дисперсия известна или большой объем выборки)
(дисперсия известна или большой объем выборки)
| 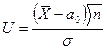 (по таблице Лапласа)
1) (по таблице Лапласа)
1) 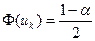 2)
2) 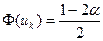 3)
3) 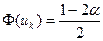
|
1) 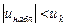 принимаем Н0
2) принимаем Н0
2) 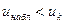 принимаем Н0
3) принимаем Н0
3) 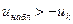 принимаем Н0 принимаем Н0
|
H0: 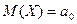 1)
1) 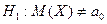 2)
2) 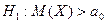 3)
3) 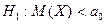 (дисперсия неизвестна или малый объем выборки)
(дисперсия неизвестна или малый объем выборки)
| 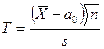 Распределение Стьюдента с k степенями свободы
1)
Распределение Стьюдента с k степенями свободы
1) 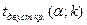 , k=n-1
2) , k=n-1
2) 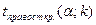 , k=n-1
3) , k=n-1
3) 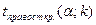 , k=n-1 , k=n-1
|
1) 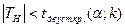 принимаем Н0
2) принимаем Н0
2) 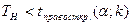 принимаем Н0
3) принимаем Н0
3) 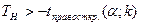 принимаем Н0 принимаем Н0
|
H0: 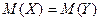 1)
1) 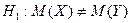 2)
2) 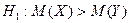 3)
3) 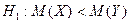 (дисперсии известны или большой объем выборки, выборки независимы)
(дисперсии известны или большой объем выборки, выборки независимы)
| 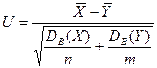 (по таблице Лапласа)
1)
(по таблице Лапласа)
1) 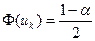 2)
2) 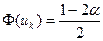 3)
3) 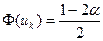
|
1) 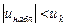 принимаем Н0
2) принимаем Н0
2) 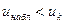 принимаем Н0
3) принимаем Н0
3) 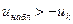 принимаем Н принимаем Н
|
H0: 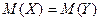 1)
1) 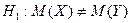 2)
2) 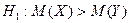 3)
3) 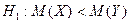 (дисперсии неизвестны и одинаковы, малый объем выборки, выборки независимы)
(дисперсии неизвестны и одинаковы, малый объем выборки, выборки независимы)
| 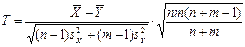 Распределение Стьюдента с k степенями свободы,
Распределение Стьюдента с k степенями свободы, 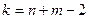 1)
1) 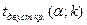 ,
2) ,
2) 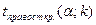 ,
3) ,
3) 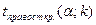 , ,
|
1) 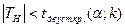 принимаем Н0
2) принимаем Н0
2) 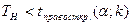 принимаем Н0
3) принимаем Н0
3) 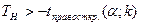 принимаем Н0 принимаем Н0
|
H0: 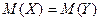 1)
1) 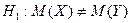 (нормально распределенные генеральные совокупности одинакового объема, зависимые выборки, дисперсии неизвестны)
(нормально распределенные генеральные совокупности одинакового объема, зависимые выборки, дисперсии неизвестны)
| Сводим к одной выборочной средней:
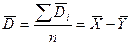
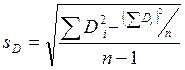
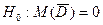
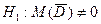 См. строку II данной таблицы
См. строку II данной таблицы
| |
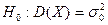 1)
1) 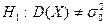 2)
2) 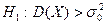 3)
3) 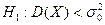 (нормально распределенные генеральные совокупности)
(нормально распределенные генеральные совокупности)
| 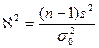 Распределение
Распределение 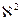 с k=(n-1) степенями свободы
1) с k=(n-1) степенями свободы
1) 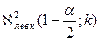 , , 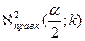 2)
2) 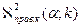 3)
3) 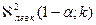
|
1) 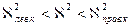 , принимаем Н0
2) , принимаем Н0
2) 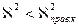 , принимаем Н0
3) , принимаем Н0
3) 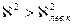 , принимаем Н0 , принимаем Н0
|
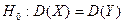 1)
1) 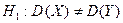 2)
2) 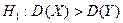 (обозначим так, чтобы
(обозначим так, чтобы 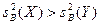 .
Выборки независимы и распределены нормально) .
Выборки независимы и распределены нормально)
| 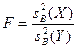 Распределение Фишера - Снедекора с k1=n1-1 и k2=n2-1 степенями свободы
1)
Распределение Фишера - Снедекора с k1=n1-1 и k2=n2-1 степенями свободы
1) 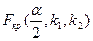 2)
2) 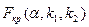
|
1) 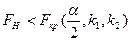 , принимаем Н0
2) , принимаем Н0
2) 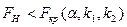 , принимаем Н0 , принимаем Н0
|
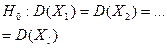 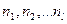 - объемы выборок нормально распределенных ген.совокупн.; - объемы выборок нормально распределенных ген.совокупн.;
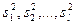 - испр.выб.дисперсии; - испр.выб.дисперсии;
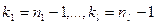 - число степеней свободы (все больше 2) - число степеней свободы (все больше 2)
| 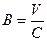 - критерий Барлетта
Распределение - критерий Барлетта
Распределение 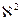 с k=(l-1) степенями свободы (приближенно)
Где с k=(l-1) степенями свободы (приближенно)
Где 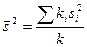 , ,
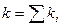 , ,
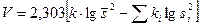 , ,
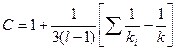
|
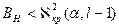 , принимаем Н0 , принимаем Н0
|
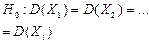 n – объем каждой из выборок нормально распределенных ген.совокупн.;
n – объем каждой из выборок нормально распределенных ген.совокупн.;
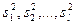 - испр.выб.дисперсии; - испр.выб.дисперсии;
| 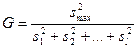 -критерий Кочрена
Таблица критических точек Кочрена -критерий Кочрена
Таблица критических точек Кочрена
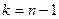 - число степеней свободы - число степеней свободы
|
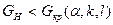 , принимаем Н0 , принимаем Н0
|
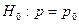 1)
1) 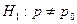 2)
2) 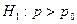 3)
3) 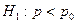
| 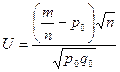 (по таблице Лапласа)
1) (по таблице Лапласа)
1) 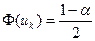 2)
2) 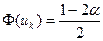 3)
3) 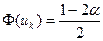
|
1) 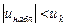 принимаем Н0
2) принимаем Н0
2) 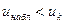 принимаем Н0
3) принимаем Н0
3) 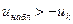 принимаем Н0 принимаем Н0
|
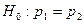 1)
1) 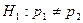 2)
2) 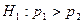 3)
3) 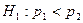 (Биномиальные распределения)
(Биномиальные распределения)
| 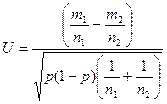
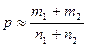 (по таблице Лапласа)
1)
(по таблице Лапласа)
1) 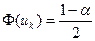 2)
2) 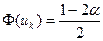 3)
3) 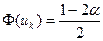
|
1) 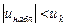 принимаем Н0
2) принимаем Н0
2) 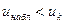 принимаем Н0
3) принимаем Н0
3) 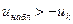 принимаем Н0 принимаем Н0
|
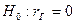
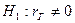
| 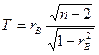 Распределение Стьюдента с k степенями свободы
Распределение Стьюдента с k степенями свободы
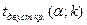 , k=n-2 , k=n-2
|
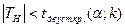 принимаем Н0 принимаем Н0
|






