Критерий однородности выборок

Имеется независимых выборок, объемом n_i каждая (i=1,2,…, );

.

H₀: выборки извлечены из одной и той же совокупности (т.е. выборки однородны)

Н₁: выборки неоднородны.

Критерий проверки гипотезы - случайная величина, имеющая ² – распределение с степенями свободы.

Алгоритм проверки основной гипотезы :

1) данные каждой выборки группируются в одиночных групп (интервалов); подсчитывают число m_ij наблюдений из i- й выборки, попавших в j -ю группу:

2) подсчитывают вероятность p_j принадлежности отдельного результата к каждой группе: ;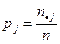

затем вычисляют ожидаемые частоты

3) вычисляют величину

При >5 это ² – распределение с степенями свободы.

4) если - гипотезу H₀ принимают.

если - гипотезу H₀ отвергают.

 

§15. Проверка гипотезы о виде распределения случайной величины. Критерий согласия (хи – квадрат)

Критерий согласия – это критерий проверки гипотезы о предполагаемом неизвестном распределении. Рассмотрим критерий Пирсона, который отвечает на вопрос: «З начимо ли расхождение эмпирических и К теоретических частот?».

Оценкой функции плотности распределения случайной величины Х служит относительная частота - , где – объем выборки; - число наблюдений попавших в интервал , на которые разбита вся числовая прямая. По гистограмме делают предположения о законе распределения (при подходящем выборе шага , она напоминает функцию плотности случайной величины Х)

Пусть Х и Y – независимые выборки.

Выдвигаем основную гипотезу:

H₀: случайная величина Х подчиняется закону распределения F(x).

Н₁: случайная величина Х не подчиняется закону распределения F(x).

Алгоритм проверки основной гипотезы:

1) вся область разбивается на k интервалов 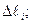(в каждом должно не меньше 5 наблюдений);

n_i – эмпирическое количество элементов, попавших в (эмпирическая частота)

2) вычисляем вероятность по известной функции F(x) при условии справедливости основной гипотезы ;

- теоретическое количество значений случайной величины, попавших в интервал (теоретическая частота или выравнивающая частота)

		…
		…
		…

 

3) в качестве меры расхождения между эмпирическими и теоретическими частотами используют критерий Пирсона:

,

где - теоретические частоты.

4) находят наблюдаемое значение критерия

По таблице - распределения находят критическую точку - число степеней свободы, - количество параметров, вычисленных по выборке; 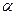- уровень значимости).

Если гипотезу H₀ отвергают.

Если 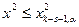гипотезу H₀ принимают.

В частности, если предполагать, что генеральная совокупность распределена нормально, то выравнивающие частоты могут быть найдены по формуле:

n =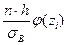

где n – объем выборки; h – шаг выборки; s_В - выборочное среднее квадратическое отклонение; z_i= ( - выборочная средняя); j(z)= - плотность нормированного нормального распределения.

1.

Замечание: объем выборки должен быть достаточно велик (n³50). Причем критерий только дает согласие, поэтому для улучшения можно повторить опыт, увеличить число наблюдений и т.д.

 

Пример 34. Дано статистическое распределение выборки: в первой строке указаны выборочные варианты х _i, а во второй строке – соответственные частоты n _i количественного признака Х). Требуется, пользуясь критерием Пирсона, при уровне значимости a=0,05, установить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с данными выборки объема n=100.

хi
ni

 

Решение: Для применения критерия Пирсона составим таблицу:

xi	zi= =	j(zi)	n	ni	n - ni
	-1,90	0,0656	5,19		0,19	0,01
	-1,11	0,2155	17,06		2,06	0,25
	-0,32	0,3790	29,96		-10,04	3,36
	0,47	0,3572	28,24		3,24	0,37
	1,26	0,1804	14,26		6,26	2,75
	2,06	0,0478	3,78		-0,22	0,01
	2,85	0,0069	0,55		-2,45	10,91

 

Здесь: =284, s_В = =12,65 вычислены в примере 33; n=100 по условию; h=270-260=10 – шаг выборки; n = = 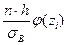=79,05×j(z_i).

Таким образом, получаем, что =17,66.

По таблице критических точек распределения приложения 4 при заданном a=0,05 и k = s – 3 = 7 – 3 = 4 (s – число групп выборки) находим (a; k)= (0,05; 4)=9,5.

Т.к. > (17,66 > 9,5), то гипотеза о нормальном распределении генеральной совокупности не согласуется с данными выборки.

Ответ: гипотеза не согласуется с данными выборки.

 

Лекция 3

Статистический анализ. Регрессионный и корреляционный анализ. Корреляция и причинная зависимость, коэффициент корреляции. Регрессионные модели. Множественная линейная регрессия