I. Сравнение двух средних произвольно распределенных генеральных совокупностей (большие независимые выборки)
Если n≥30, m≥30, то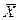 
и 
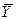, распределены приближенно нормально, а выборочные дисперсии – достаточно хорошие оценки генеральных дисперсий, то есть дисперсии можно считать известными.
Тогда критерий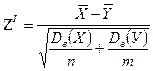 
- случайная величина, распределенная приближенно нормально, 
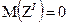(при условии справедливости 
); 
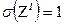(если выборки независимы)
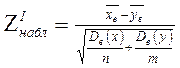- наблюдаемое значение критерия, вычисленное по конкретным выборочным данным.
Правило 1: : 
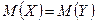- основная гипотеза.
: 
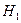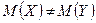- конкурирующая гипотеза.
По таблице функции Лапласа находим критическую точку двусторонней критической области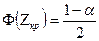 
.
Если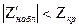 
- нет оснований отвергнуть 
,
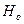если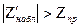 
- отвергают
Правило 2: : 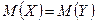- основная гипотеза
: 
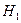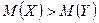- конкурирующая гипотеза.
По таблице функции Лапласа находим критическую точку правосторонней критической области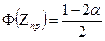 
.
Если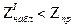 
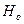- нет оснований отвергнуть ,
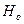если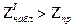 
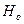- отвергают
Правило 3: : 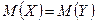- основная гипотеза
: 
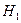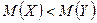- конкурирующая гипотеза.
По таблице функции Лапласа находим критическую точку правосторонней критической области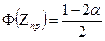
Если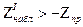 
- нет оснований отвергнуть ,
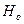если 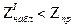- 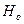отвергают.
II. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)
Пусть Х и Y – распределены нормально, дисперсии неизвестны, но есть основания предполагать, что D(X)=D(Y).
(можно проверить гипотезу о равенстве дисперсий по критерию Фишера- Снедекора)
Критерий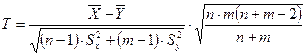 
имеет t-распределение Стьюдента с k=n+m-2 степенями свободы; 
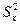и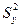 
- направленные дисперсии.
Правило 1. : 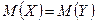- основная гипотеза,
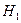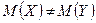: - конкурирующая гипотеза.
Критическая область – двусторонняя.
t(α;k) – правая граница критической области;
-t(α;k) – левая граница критической области. (здесь α – уровень значимости; k=m+m-2 – степень свободы)
Если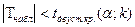 
- принимаем основную гипотезу
Если 
- отвергаем основную гипотезу
Правило 2. : 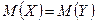- основная гипотеза,
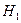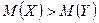: - конкурирующая гипотеза.
Критическая область – правосторонняя.
Если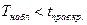 
- принимаем основную гипотезу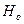
Если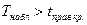 
- отвергаем основную гипотезу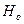
Правило 3. : 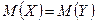- основная гипотеза,
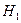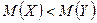: конкурирующая гипотеза.
Критическая область- левосторонняя.
Если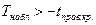 
- принимаем основную гипотезу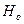
Если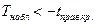 
- отвергаем основную гипотезу .
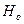III. Сравнение двух средних нормальных генеральных совокупностей с неизвестными дисперсиями (зависимые выборки)
Пусть Х и Y – распределены нормально, зависимые выборки (например, проверка одних и тех же деталей на разными приборами или экспертами). Объем выборок при этом одинаковый и равен 
.
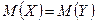: - основная гипотеза,
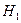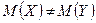: - конкурирующая гипотеза
Сведем к одной выборочной средней, обозначив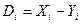 
:
.
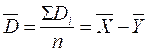В этих обозначениях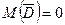 
=> :
: 
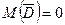
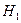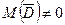
Задача свелась к задаче сравнения одной выбор средней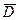 
с гипотетическим значением ,
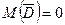где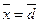 
; 
; 
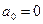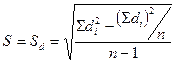- исправленное среднее квадратическое отклонение.
Тогда критерий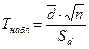 
- случайная величина, имеющая распределение Стьюдента с k=n-1 степенями свободы.
Пример 1. Пример 1. Фирма утверждает, что средний срок безотказной работы изделия 2900ч. Для выборки из 50 изделий средний срок равен 2720 ч. При выбор средн кв отклонения 700ч. При 5% уровне значимости проверить гипотезу о том, что 2900 ч – математических ожиданий
Решение.
Критерий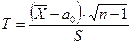 
- случайная величина, имеющая распределение Стьюдента.
: 
: 
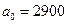
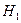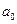<2900
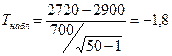
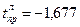- левосторонняя критическая точка
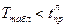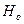=> отвергается
Пример 2. Фирма предлагает автоматы по разливу напитков. При выборе n=16 найдено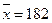 
г дозы в стакане автоматом №1. По выборке m=9 найдена 
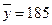г дозы, наливаемой в стакан автоматом №2. По утверждению изготовить сл/в наливаемой дозы имеет нормальный знач распределения с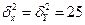 
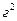. Можно ли считать, что автомат №2 наливает в стакан большую дозу напитка.
Решение.
: 
; : 
; 
; 
; 
=> 
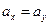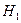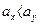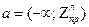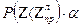
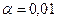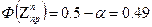
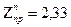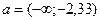
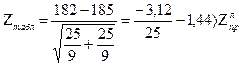=> принимается
