Элементы теории корреляции. Уравнение прямой регрессии у на Х по сгруппированным данным.

 

Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины от одной или нескольких других величин.

Статистическая зависимость – это зависимость, при которой изменение одной величины влечет изменение распределения другой.

Корреляционная зависимость – это статистическая зависимость, при которой изменение одной из величин влечет изменение среднего значения другой.

 

При большом числе наблюдений одно и то же значение Х может встретиться n_x раз, а одно и то же значение У – n_y раз, тогда одна и та же пара (Х, У) может встретиться n_xy раз. В этом случае данные группируют, т.е. подсчитывают частоты n_x, n_y, n_xy.

Все сгруппированные данные записывают в виде таблицы, которая называется корреляционной, в первой строке и первом столбце которой перечисляются наблюдаемые значения признаков Х и У. На пересечении строк и столбцов находятся n_xy наблюдаемых пар значений признаков. В последней строке и последнем столбце записаны суммы частот столбцов и строк, т.е. n_x и n_y. В крайней нижней правой клетке помещена сумма всех частот n – общее число всех наблюдений (аналог объема выборки).

!

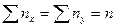
Например, рассмотрим корреляционную таблицу вида:

У	Х	ny
		-
	-
			-	-
nx					n=60

Здесь, например, пара (30, 4) наблюдалась 7 раз, а само значение признака Х=30 наблюдалось всего 13 раз и т.д.

Регрессией У на Х, т. е. условным математическим ожиданием случайной величины У относительно случайной величины Х, называется функция вида М(У/Х) = f(х).

Оценкой этой функции является выборочное уравнение регрессии: =f^*(x), причем на практике чаще используются уравнения линейной регрессии.

Выборочное уравнение прямой линии регрессии Y на Х по

сгруппированным данным имеет вид:

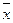где - условная средняя; и - выборочные средние признаков Х и Y; s_х и s_у – выборочные средние квадратические отклонения; r _B – выборочный коэффициент корреляции.

Если данные наблюдений над признаками Х и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам u и v: u_i = , v_j = , где С₁ и С₂ – ложные нули (С₁ – значение признака Х с наибольшей частотой, С₂ – значение признака Y с наибольшей частотой), h₁ – шаг варианты Х, h₂ – шаг варианты Y. Тогда выборочный коэффициент корреляции вычисляют по формуле: r_B = .

Величины 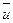, , s_u, s_v можно найти методом произведений, а при малом числе данных – по определению, а именно , ,

s_u = , s_v = , где , . После чего можно найти величины, входящие в уравнение регрессии, по формулам: , , s_х = s_uh₁, s_y = s_vh₂.

Метод нахождения

Для этого составляют корреляционную таблицу в условных вариантах, после чего составляют специальную таблицу:

1. В каждой клетке, в которой n_uv ¹ 0, в правом верхнем углу записывают произведение n_uv на u.

2. Складывают все числа, помещенные в этих правых верхних углах и их суммы записывают в столбец U.

3. Умножают варианту v на U по строкам и записывают результаты в последнем столбце vU.

4. Суммируют элементы последнего столбца. Полученная сумма и равна .

5. Для контроля аналогичные вычисления производят по столбцам (в левых нижних углах клеток, в которых n_uv ¹ 0).

Пример 5. Найти по данным корреляционной таблицы:

Y	X	ny
	-		-	-	-	-
				-	-	-
	-				-	-
	-	-				-
	-	-	-	-
nx							n=100

Решение: составим корреляционную таблицу в условных вариантах (в качестве ложных нулей лучше взять х₄=33, т.е. С₁=33, и у₃=175, т.е. С₂=175):

V	U	nv
-3	-2	-1
-2	-		-	-	-	-
-1				-	-	-
	-				-	-
	-	-				-
	-	-	-	-
nu							n=100

Теперь, по этой таблице составим еще одну – расчетную для вычисления :

U V	-3	-2	-1				U=	vU
-2		-2 -2					-2
-1	-3 -1	-4 -2	-5 -5				-12
		-6	-12				-18
			-1
V=	-1	-4	-4					48
uV							48	конт- роль

 

Итак, в правых нижних углах получили 48, значит = 48.

Ответ: = 48.

 

 

Пример 6. Найти выборочное уравнение прямой линии регрессии Y на Х 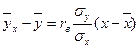по данной корреляционной таблице:

 

 

Y	X	ny
	-		-	-	-	-
				-	-	-
	-				-	-
	-	-				-
	-	-	-	-
nx							n=100

 

Решение: составим корреляционную таблицу в условных вариантах (в качестве ложных нулей лучше взять х₄=33, т.е. С₁=33, и у₃=175, т.е. С₂=175):

V	U	nv
-3	-2	-1
-2	-		-	-	-	-
-1				-	-	-
	-				-	-
	-	-				-
	-	-	-	-
nu							n=100

 

1. Вычислим теперь 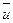, , s_u, s_v:

= = -0,13;

= =0,22;

= =0,81;

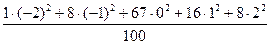= =0,6, значит,

s_u = 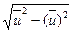= =0,89; s_v = = =0,74.

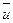Найдем выборочный коэффициент корреляции r_B = , где = 48 (см. пример 35); = -0,13; =0,22; s_u = 0,89; s_v = 0,74. Тогда

r_B = =0,73.

2. С₁=33, h₁=23 – 18=5; C₂=175, h₂=150 – 125=25.

Значит, можно вычислить 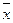, , s_х , s_y:

= -0,13×5+33= 32,35; =0,22×25+175=180,5;

s_х = s_uh₁ = 0,89×5=4,45; s_y = s_vh₂ = 0,74×25=18,5.

Подставим полученные значения в уравнение прямой линии регрессии Þ Þ =3,03х +82,48 – искомое уравнение.

Ответ: =3,03х +82,48.

 

 

Лекция 4

Статистический анализ. Многомерный статистический анализ. Дисперсионный анализ. Однофакторный и двухфакторный дисперсионный анализ. Дискриминантный анализ; кластерный анализ; факторный анализ