Теория гомоцентрических сфер Эвдокса 3 страница

365 1/4 — 1/300 = 365,24667 дня = 365 дней 5 час. 55 мин. 12 сек.

Как указывают историки астрономии, это значение превышало истинное на 6 мин. 13 сек.: в эпоху Гиппарха длительность тропического года составляла 365 дней 5 час. 48 мин. 59 сек. Учитывая, однако, сравнительно примитивные средства наблюдений, которыми пользовались греческие астрономы, такую ошибку можно считать вполне извинительной. Установление моментов равноденствия представляло в то время немалые трудности, и даже Птолемей писал, что здесь могут встречаться ошибки «больше одной четверти дня»^[235]. Длина тропического года, принятая Гиппархом, была средним статистическим значением, выведенным из множества наблюдений, производившихся как греческими, так и вавилонскими астрономами.

В качестве двух других величин, которые были ему нужны, Гиппарх принял промежуток времени между весенним равноденствием и летним солнцестоянием (астрономическая весна) и промежуток между летним солнцестоянием и осенним равноденствием (астрономическое лето). Эти промежутки, согласно его данным, были соответственно равны девяносто четырем с половиной и девяносто двум с половиной дням.

На этих трех величинах Гиппарх строит всю теорию Солнца. Долгота апогея Солнца (если долготу точки весеннего равноденствия принять за 0°) оказалась, согласно его теории, равной 65°30", а эксцентриситет (т. е. отношение расстояния между центрами Земли и Солнца к радиусу эксцентра Солнца) составил величину е =1/24=0,04166. Кроме того, теория Гиппарха давала возможность определить видимую долготу Солнца в любой момент времени. Отметим, кстати, что в теории Гиппарха Солнце движется точно по эклиптике, откуда следует, что он понимал ошибочность мнения Эвдокса о широтных колебаниях положения Солнца (о чем было сказано выше в связи с теорией гомоцентрических сфер). Между тем это ошибочное мнение оказалось очень живучим: в том или ином виде оно повторялось позднейшими компиляторами, например Плинием, Теоном и Марцианом Капеллой. В чем заключалась причина этой живучести? Может быть, в том, что с помощью такого предположения некоторые астрономы (еще до Гиппарха) пытались объяснить расхождение между длительностью тропического и сидерического года?

Такое расхождение действительно существовало, но его следовало объяснить не широтными колебаниями Солнца, а явлением предварения равноденствий (прецессии), которое принадлежит к числу наиболее блестящих открытий античной астрономии и тоже связано с именем Гиппарха. А именно, сравнивая свои наблюдения с наблюдениями александрийских астрономов начала III в. Аристилла и Тимохариса, Гиппарх обнаружил, что за протекшие с тех пор полтораста лет точки весенного и осеннего равноденствий переместились вдоль эклиптики с востока на запад примерно на 2°. Это значение довольно точно соответствует истинному (согласно измерениям недавнего времени прецессия составляет около 50,3" в год). Небесная механика нашего времени объясняет явление прецессии характерным для любого волчка медленным движением оси вращения по круговому конусу. Этого Гиппарх, разумеется, знать не мог, но о том, что он сознавал важность своего открытия, свидетельствует написанный им по этому поводу и упоминаемый Птолемеем в «Альмагесте» специальный трактат, имевший заглавие «Об изменениях точек солнцестояния и равноденствия»^[236].

Помимо этого трактата, Птолемей называет еще два сочинения Гиппарха: «О длине года» и «Об интеркаляции месяцев и дней»^[237]; в последнем из них излагался уточненный лунно-солнечный календарь, составленный с учетом длин тропического года и лунного месяца, вычисленных Гиппархом. В основе этого календаря лежал цикл, который точно делился на 304 года и 3760 лунных месяцев. Календарь этот имел чисто теоретическое значение и никем никогда не использовался.

Большое внимание уделил Гиппарх также теории движения Луны, хотя мы не знаем, было ли у него специальное сочинение на эту тему. Здесь он встретился со значительно большими трудностями, чем при построении теории движения Солнца. Судя по изложению Птолемея, эти трудности так и не были до конца им преодолены, хотя в его распоряжении имелся богатый материал, накопленный халдейскими астрономами, на протяжении ряда столетий наблюдавшими лунные затмения. Эти данные Гиппарх мог сравнить с результатами, полученными александрийскими наблюдателями, а также со своими собственными наблюдениями: известно, что в промежутке между 146 и 135 гг. до и. о. Гиппарх наблюдал несколько лунных затмений. Он определил периоды обращения Луны, получив для них следующие значения: синодический период: 29 дней 12 час. 44 мин. 3,3 сек. сидерический период: 27 дней 7 час. 43 мин. 13,1 сек. Оба этих значения с точностью до одной секунды совпадают с истинными значениями и практически не отличаются от значений, записанных в вавилонских таблицах.

Разрабатывая теорию движения Луны, Гиппарх мог воспользоваться как моделью подвижного эксцентра, так и моделью эпициклов. Птолемей в «Альмагесте» подчеркивает эквивалентность обеих моделей, однако для детального изложения теории Гиппарха предпочитает гипотезу эпициклов, резервируя эксцентры для объяснения того, что Гиппарх обозначил в качестве «второй аномалии» Луны. Итак, в изложении Птолемея теория движения Луны Гиппарха выглядит следующим образом.

Движение Луны происходит по эпициклу, центр которого перемещается по кругу (деференту), не лежащему в плоскости эклиптики (как это имеет место в случае Солнца), а наклоненному по отношению к этой плоскости под углом 5°. Сам деферент медленно вращается вокруг оси эклиптики так, что узлы (точки пересечения деферента с эклиптикой) совершают полный оборот в течение 18 2/3 лет. Центр эпицикла перемещается по деференту в прямом направлении (т. е. с запада на восток), в то время как Луна движется по эпициклу в обратном направлении. Периоды обращения Луны по деференту и эпициклу принимаются слегка различными, а именно в течение одного года движение по эпициклу отстает от (среднего) движения по деференту на 3°. Отношение радиуса эпицикла к радиусу деферента в теории Гиппарха оказалось равным 5 1/4: 60=0,0875.

Мы ограничимся перечислением этих основных положений теории Гиппарха, поскольку более детальное ее изложение потребовало бы сложных геометрических построений, приводимых Птолемеем в «Альмагесте». Читателя, который пожелал бы разобраться в этих построениях, мы отсылаем к соответствующим курсам истории астрономии.

Теория Луны Гиппарха была, бесспорно, замечательным достижением эллинистической науки. Но насколько точно решалась этой теорией проблема «спасения явлений», т. е. проблема объяснения видимых движений Луны по небесному своду? Она давала возможность достаточно хорошо предвычислять положения Луны в моменты полнолуния и новолуния. Гиппарх пробовал проверить ее также для тех моментов, когда Луна находится в первой или последней четверти. Он обнаружил, что в этих случаях видимые положения Луны иногда совпадают с вычисленными, иногда же более или менее значительно отличаются от них. Он предположил, что здесь мы встречаемся еще с одной аномалией, которую он и назвал «второй аномалией» Луны. Исследование природы этой аномалии он оставил астрономам последующих поколений. Эта задача, как мы увидим ниже, была решена Птолемеем в «Альмагесте».

Что касается пяти остальных планет, то здесь Гиппарху не удалось создать теорию, которая могла бы его удовлетворить. Причины этой неудачи анализируются Птолемеем в «Альмагесте». Перечислив трудности, с которыми сталкивается наблюдатель, изучающий прямые и попятные движения планет, Птолемей продолжает: «Я полагаю, что Гиппарх, для которого истина была дороже всего на свете, именно по указанным причинам, а особенно потому, что он не получил от своих предшественников такого количества точных наблюдений, которые он оставил нам, ограничился разработкой гипотез, относящихся к Солнцу и Луне, доказав, что их движение может быть сведено к комбинациям круговых и равномерных движений; что же касается пяти планет, то, по крайней мере в дошедших до нас его сочинениях, он даже не приступил к решению аналогичной задачи, ограничившись систематизацией имевшихся в его распоряжении наблюдений и показав, что эти наблюдения не согласуются с гипотезами математиков того времени. Ибо он, по-видимому, считал, что ему не только удалось показать, что каждая планета обладает двумя аномалиями или что у каждой из них обнаруживаются попятные движения различной длины, в то время, как другие математики проводили свои геометрические доказательства, исходя из предположения о наличии всего лишь одной аномалии, характеризующейся одной дугой попятного движения; он, кроме того, полагал, что эти явления не могут быть представлены с помощью эксцентрических или концентрических по отношению к эклиптике кругов или с помощью эпициклов, вращающихся на этих кругах, или даже путем комбинации обоих методов…»^[238].

Для того чтобы сделать изложение заслуг Гиппарха более полным, следует сказать еще несколько слов. В своих вычислениях Гиппарх широко пользовался тригонометрическими соотношениями, правда без тех обозначений, которые получили хождение в математике нового времени. Вместо таблиц синусов и тангенсов он составил таблицу хорд, в которой относительные длины хорд были даны в зависимости от стягиваемых ими углов. Предполагается, что эта таблица содержалась в написанной им книге «О теории прямых в круге»^[239]. К сожалению, ни эта книга, ни таблица хорд до нас не дошли, поэтому мы не можем сказать, каким способом Гиппарх вычислял значения хорд, включенные в таблицу. Следует при этом отметить, что Гиппарх уже широко пользовался вавилонской системой деления круга на 360° и затем на минуты и секунды; с тех пор эта система вошла во всеобщее употребление.

Немалый вклад был внесен Гиппархом и в звездную астрономию. Он составил каталог неподвижных звезд, содержавший, как предполагают, около 850 звезд, места которых на небесном своде определялись их эклиптическими координатами (долготой и широтой относительно эклиптики). Впоследствии Плиний писал, что работа по составлению каталога была предпринята Гиппархом после того, как на небе вспыхнула новая звезда. Мы не знаем, так ли это было на самом деле. Что касается приборов, которыми пользовался Гиппарх при своих наблюдениях, то в основном это была, по-видимому, диоптра, описанная впоследствии Проклом и состоявшая из двух пластин с вырезами, укрепленных на длинном (около четырех футов) бруске, вдоль которого был вырезан узкий желобок.

От Гиппарха до Птолемея

Гиппарх был последним великим астрономом «золотого века» эллинистической науки. В отличие от, скажем, Эвдокса, мы ничего не знаем о школе Гиппарха. О том, были ли у него преемники или ученики, источники хранят полное молчание. Вероятнее всего такие ученики существовали, но ни один из них не прославил себя сколько-нибудь значительными открытиями и не оставил потомству никаких сочинений. Это были, по-видимому, скромные наблюдатели, незаметно продолжавшие дело их учителя и накапливавшие данные, совокупность которых позволила позднее Птолемею завершить величественное здание геоцентрической системы мира, основы которого были заложены Гиппархом.

Наряду с этим необходимо отметить следующее кардинальной важности обстоятельство. Именно в это время происходит изменение характера или, если угодно, стиля эллинистической науки. Вместо ученого-исследователя, какими были Аристарх, Аполлоний Пергский, Гиппарх и труды которых были нужны и понятны лишь узкому кругу профессионалов-специалистов, на первый план выступает энциклопедист-популяризатор — по сути дела, не ученый, а псевдоученый. Потребность в научных энциклопедиях, содержащих популярное изложение не столько даже достижений той или иной науки, сколько мнений ученых предшествующих эпох, достигла, как мы увидим ниже, своего расцвета в эпоху римского господства. Но уже в рассматриваемую нами эпоху II–I вв. до н. э. эта потребность стала настоятельно ощущаться прежде всего благодаря тому, что наукой начали интересоваться достаточно широкие и разумеется, профессионально неподготовленные круги тогдашней общественной элиты. Этот интерес надлежало удовлетворить.

Ключевой фигурой этого переломного периода была фигура знаменитого стоика-эклектика Посидония. Мы знаем заглавия ряда трактатов Посидония: «Физические рассуждения», «О метеорах», «Об океане», «О величине Солнца» и т. д. Большой популярностью пользовался также его комментарий к «Тимею» Платона. Ни одна из этих книг до нас не дошла, но об их содержании мы можем составить представление по сочинениям позднейших авторов, находившихся под его влиянием. Хотя сам Посидоний и не писал энциклопедий в духе Варрона или Плиния Старшего, тем не менее именно от него исходили мощные импульсы для возникновения такого рода литературы. Если охарактеризовать облик Посидония-ученого одним словом, то это был не столько естествоиспытатель, сколько натурфилософ — и не в том смысле, в каком это слово зачастую употребляется применительно к досократикам, а, скорее, в смысле натурфилософии нового времени, для которой естествознание использовалось в качестве иллюстрации или обоснования некоей общефилософской концепции. В основе концепции Посидония лежала идея всеобщей гармонии и взаимосвязи всех природных процессов. Здесь, однако, мы не будем вдаваться в характеристику философских воззрений Посидония, а ограничимся кратким рассмотрением тех его работ, которые имели прямое или косвенное отношение к астрономической науке.

Хотя основная деятельность Посидония протекала на острове Родос — там, где примерно за полвека до него жил и работал Гиппарх, упоминания о теории эпициклов и эксцентров мы в ссылках на Посидония не находим. Вероятно, он не обладал достаточной математической подготовкой, для того чтобы суметь разобраться в геометрических построениях, с помощью которых Гиппарх «спасал явления». Посидония занимала другая проблематика — форма и размеры Земли, величина Солнца, расстояния от Земли до небесных светил, порядок расположения планет и т. д. Все эти вопросы нашли отражение в сочинениях популяризаторов последующей эпохи — Клеомеда, Гемина и других авторов, находившихся под большим влиянием Посидония.

Что касается формы Земли, то этот вопрос со времени Платона уже не вызывал сомнения у серьезных ученых (исключение составляла, пожалуй, лишь школа Эпикура, во многом сохранявшая архаичные воззрения на устройство мира). Убедительные аргументы в пользу шарообразности Земли приводятся в трактате «О небе» Аристотеля^[240]. Эти аргументы, однако, оставались достоянием лишь небольшого числа ученых, и их еще следовало внедрить в сознание широких кругов античного общества. Имея в виду именно эту цель, Посидоний подробно разбирает различные гипотезы о форме Земли, предлагавшиеся ранними мыслителями, и показывает их несостоятельность. Обсуждение проблемы шарообразности Земли является одной из основных тем позднейших популярных сочинений по астрономии, писавшихся под влиянием Посидония. О том, каким образом в период эллинизма астрономы определяли размеры земного шара, уже было сказано в четвертой главе.

Следующей проблемой, которая их интересовала, была проблема расстояния от Земли до других небесных тел. Решение этой проблемы лежало за пределами возможностей геоцентрической модели, основанной на представлениях об эпициклах и эксцентрах, поскольку (как уже было отмечено выше) эта модель оперировала лишь с проекциями движений небесных светил на небесную сферу, о размерах которой не делалось никаких предположений.

Прежде всего нужно было решить вопрос о порядке расположения небесных светил. Еще в пифагорейской астрономии было принято считать, что ближе всего к Земле находится Луна, вслед за которой идет Солнце, а уже за ним расположены пять планет, начиная от Меркурия и кончая Сатурном. Пифагорейцы полагали, что относительные расстояния между орбитами этих светил соответствуют интервалам музыкальной гаммы (соответствующие цифры приводятся многими позднейшими авторами, причем их данные сильно расходятся, так что реконструкция исходной пифагорейской схемы представляет значительные трудности). Согласно Платону (в «Тимее»), разности планетных орбит пропорциональны числам 1, 2, 3, 4, 8, 9, 27^[241]; приняв эту последовательность, Платон, очевидно, следовал какой-то пифагорейской традиции, хотя последняя из цифр этого ряда не может соответствовать ни одной из музыкальных нот. Пифагорейское учение о небесной гармонии было раскритиковано Аристотелем о трактате «О небе»^[242], хотя никакой альтернативной гипотезы в отношении расстояния между орбитами небесных светил Аристотель не предлагает; что же касается порядка расположения планет, то в этом вопросе он следует установившейся традиции. Эта традиция была нарушена в эллинистическую эпоху, когда Меркурий и Венера были помещены между Луной и Солнцем; мы не знаем, кем был установлен этот новый порядок; во всяком случае, решающую роль в этом изменении сыграли более точные данные о движении обеих внутренних планет. Что же касается учения о небесной гармонии, то, несмотря на критику Аристотеля, оно продолжало сохранять популярность не только в течение всей поздней античности, но и в средние века.

Начиная с Эвдокса, греческие астрономы неоднократно пытались оценить как абсолютные расстояния от Земли до Луны и Солнца, так и истинные размеры этих небесных светил (мы оставляем без рассмотрения псевдонаучные спекуляции на эту тему Анаксимандра, пифагорейцев и других ранних мыслителей). Имеются сообщения, что ученик Платона Филипп Опунтский (которого некоторые исследователи считают автором «Послезакония», обычно включаемого в собрание сочинений Платона) написал трактат о расстояниях от Земли до Луны и Солнца, о размерах этих небесных тел, а также о лунных затмениях и о планетах. Однако ничего более точного о содержании этого трактата мы не знаем. Первая оценка относительных размеров Луны и Солнца принадлежала, по-видимому, Эвдоксу: он полагал, что диаметр Солнца в девять раз превышает диаметр Луны, а так как видимые размеры этих небесных тел примерно одинаковы, то отсюда он заключал, что расстояние от Земли до Солнца в девять раз больше расстояния от Земли до Луны. Архимед, сообщающий эти сведения, присовокупляет, что Фидий, его отец, принимал указанное отношение равным 12: 1, Аристарх пытался доказать, что оно равно примерно 19: 1, сам же Архимед идет дальше своих предшественников и считает, что «диаметр Солнца приблизительно в тридцать раз больше диаметра Луны, но не больше»^[243]. Архимед не уточняет, каким образом обосновывалось каждое из этих отношений; мы знаем это только в отношении Аристарха, от которого дошел трактат на эту тему, о чем более подробно было рассказано нами выше.

Методика Аристарха была усовершенствована Гиппархом, о чем достаточно детальные сведения мы находим в пятой книге «Альмагеста». Результаты, полученные Гиппархом, сообщаются в популярных сочинениях Клеомеда и Теона из Смирны, живших уже в начале нашей эры. Для удобства мы объединим эти результаты (вместе с цифрами, принятыми Птолемеем) в виде следующей таблицы, причем за единицу в ней принимается средний радиус Земли (по теперешним данным=6371 км).

 

 

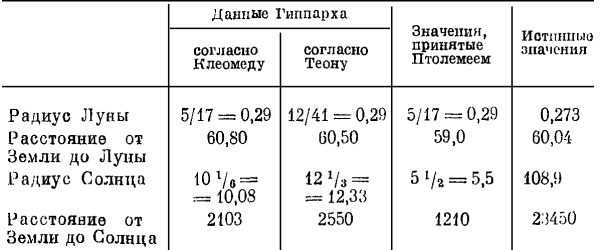
Из этой таблицы видно, что в отношении размеров Луны и расстояния от Земли до Луны значения, полученные Гиппархом, оказались поразительно точными. Гораздо хуже дело обстояло с Солнцем: здесь Гиппарх ошибался по крайней мере на порядок величины. Это объясняется тем, что измерение параллакса Солнца было задачей, превышавшей возможности античной наблюдательной техники, что, кстати сказать, сознавал и сам Гиппарх; по этой причине значения, полученные Гиппархом в отношении Солнца, были не более как весьма приблизительными прикидками. Любопытно, что в этом вопросе Птолемей допускал еще более грубые ошибки. Более или менее точное определение параллакса Солнца оказалось возможным лишь после изобретения телескопа.

Курьезная попытка определения абсолютных размеров Солнца была предпринята Посидонием. У Эратосфена где-то содержалось утверждение, что, когда Солнце находится в созвездии Рака, в Сиене (лежащей как раз на тропике Рака) предметы не отбрасывают тени в пределах площади, диаметр которой равен 300 стадиям. Это означает, что на всей этой площади солнечные лучи падают вертикально на поверхность Земли. Отсюда Посидоний заключил, что если построить конус, вершина которого совпадает с центром Земли, а его основанием является находящийся в зените диск Солнца, то тогда боковая поверхность конуса пройдет через границу указанной безтеневой области. Далее Посидоний предположил, что орбита Солнца в 10 тыс. раз превышает окружность земного шара, откуда непосредственно следовало, что диаметр Солнца должен иметь величину 10 тыс. х 300 стадиев, или, по порядку величины, около 500 тыс. км. Как это ни странно, эта цифра оказалась гораздо ближе к истинному значению диаметра Солнца (немного менее 1,4 млн км), чем результаты, полученные Гиппархом на основе предположений о параллаксе Солнца. С помощью этого же построения Посидоний сделал дальнейшие заключения о размерах земного шара. Так, радиус земного шара у него получился равным 50 тыс. стадиев (что намного превышает истинное значение), а его окружность — 300 тыс. стадиев, т. е. ровно в тысячу раз больше диаметра той области, на которой предметы не отбрасывают тени.

Из этих данных можно заключить, что Посидоний не утруждал себя точными вычислениями, а оперировал в основном круглыми цифрами (этим, вероятно, следует объяснить и совершенно произвольную цифру 10 тыс., положенную в основу его расчетов). Все это было настолько далеко от научной астрономии, что Птолемей даже не упоминает имени Посидония в связи со всей этой проблематикой. Бросается в глаза также значительное расхождение между приведенными цифрами относительно размеров земного шара и данными, полученными тем же Посидонием в результате наблюдений над звездой Канопус, о чем мы говорили выше. Популярность Посидония была, однако, настолько велика, что находившиеся под его влиянием авторы (например, Клеомед) приводили и те и другие результаты, даже не пытаясь их как-нибудь согласовать.

Как уже было отмечено на предыдущих страницах, после Гиппарха, а точнее, начиная с Посидония, наступает период, когда у нас отсутствуют сведения о серьезных астрономических исследованиях, но когда пишется целый ряд популярных астрономических сочинений, имевших, по-видимому, достаточно широкий круг читателей. На некоторых авторах этих сочинений не мешает вкратце остановиться.

Прежде всего, это Клеомед, несколько раз уже упоминавшийся на предыдущих страницах. О нем самом мы ровно ничего не знаем. Зато мы располагаем текстом его трактата по астрономии, озаглавленного достаточно серьезно: «Теория круговых движений небесных тел» (Κυκλική ϑεωρία μετεώρων). На самом же деле, это популярное сочинение, написанное, скорее всего, в I в. н. э. и носящее на себе явную печать воззрений Посидония, на которого, впрочем, сам автор неоднократно ссылается.

Трактат Клеомеда открывается несколькими аксиомами общекосмологического характера. Перечислим основные из этих аксиом:

1. «Вселенная ограничена и за пределами окружающей ее поверхности простирается безграничная пустота». Обосновывая эту аксиому, Клеомед полемизирует с перипатетической физикой; основные аргументы его полемики заимствованы у стоиков, и прежде всего, конечно, у Посидония.

2. «Земля, имеющая шарообразную форму, со всех сторон окружена Небом». Доказательство шарообразности Земли проводится Клеомедом по методу исключения: он показывает, что Земля не может быть ни плоской, ни выгнутой, ни кубической, ни пирамидальной; следовательно, она должна иметь форму шара! Наиболее убедительных аргументов в пользу этой аксиомы, таких, например, которые содержатся в аристотелевском трактате «О небе», Клеомед не приводит, ограничиваясь лишь несколькими тривиальными соображениями.

От сферичности Земли Клеомед переходит к тезису о сферичности мира в целом, заключая свои рассуждения утверждением, что сфера — наиболее совершенная из всех геометрических фигур.

3. «Земля находится в центре Вселенной».

4. «По сравнению с размерами Вселенной Земля представляется не более как точкой»^[244].

Вслед за этими аксиомами Клеомед переходит к чисто астрономическим проблемам. Несмотря на ничтожную малость Земли, он не сомневается, что она неподвижна и что Небо со всеми находящимися на нем звездами совершает вокруг нее полный оборот в течение суток. Затем Клеомед подчеркивает необходимость различать неподвижные звезды и семь небесных светил, обладающих собственным движением. Он сообщает уже приводившиеся нами сведения о размерах Луны и Солнца и о расстояниях от Земли до этих светил. Много из того, что он пишет о Гиппархе и других ученых, представляет бесспорный интерес для историка науки, поскольку оригинальные сочинения соответствующих авторов до нас не дошли. В то же время Клеомед нигде не углубляется в математические тонкости движения небесных светил, ограничиваясь таким уровнем изложения, который был бы доступен для широкого читателя, на которого, очевидно, было рассчитано его сочинение.

Другим автором примерно той же эпохи был Гемин, живший на о-ве Родос во второй половине I в. до н. э. Правда, он обладал более широким кругом интересов, чем Клеомед, и в некоторых вопросах проявлял большую самостоятельность мышления. Он написал почти полностью утерянное сочинение по математике (Περί της τών μαϑημάτων τάξεως), а также составил комментарий к трактату Посидония «О метеорах». Возможно, что дошедший до нас текст «Введение в явления» (Εισαγωγή εις τα φαινόμενα)^[245] представлял собой краткое изложение указанного комментария, составленное самим Гемином. В отличие от трактата Клеомеда этот текст не содержит общефизических (или, лучше сказать, космологических) аксиом и целиком посвящен чисто астрономическим вопросам.

Из оригинальных мыслей Гемина следует отметить утверждение, что неподвижные звезды могут находиться на различных расстояниях от Земли.

В отличие от Клеомеда и Гемина Адраст Афродисийский примыкал не к стоикам, а к перипатетикам. Он жил в I в. н. э. и в соответствии с общей тенденцией перипатетической школы этого времени написал ряд комментариев к трудам Аристотеля, в том числе и к трактату «О небе». Об астрономических воззрениях Адраста мы знаем по цитатам из его сочинений, приводимым Теоном из Смирны. Адраст был знаком с теорией Гиппарха и пытался согласовать ее с аристотелевскими представлениями о вращающихся эфирных сферах.

Все эти авторы оказали влияние на римских энциклопедистов эпохи империи, прежде всего на Плиния Старшего. Но о них мы будем говорить в специальной главе, посвященной римской науке.

Птолемей

В конце I в. н. э. начинается возрождение научной астрономии, развитие которой по каким-то не очень для нас понятным причинам приостановилось после смерти Гиппарха. Выдающимся астрономом этой эпохи (и, следовательно, первым крупным астрономом нашей эры) был Менелай Александрийский, который, правда, более известен как математик. Но его математика была, по-видимому, тесно связана с его астрономическими изысканиями. Менелай заложил основы новой науки — сферической тригонометрии. Основное его сочинение по этому вопросу — «Сферика» — дошло до нас в арабском переводе. Оно состоит из трех книг; в двух первых книгах доказываются различные теоремы о сферических треугольниках; а и третьей доказывается знаменитая «теорема о трансверсалях», нашедшая затем применение у Птолемея. Вся эта область математики разрабатывалась в качестве математического аппарата для астрономии. Но Менелай был не только теоретиком, но и астрономом-наблюдателем. Как сообщает Птолемей в «Альмагесте», во время своего пребывания в Риме Менелай занимался изучением покрытия звезд Луной^[246]. Аналогичные наблюдения производил примерно в это же время некий Агриппа в Вифинии^[247]. Эти наблюдения были использованы Птолемеем, который, сравнивая их с наблюдениями, произведенными в свое время Тимохарисом и позже Гиппархом, а также со своими собственными данными, вычислил на их основании величину смещения равноденствия (прецессии).

Следует отметить, что к этому времени происходит окончательное усвоение достижений вавилонской астрономии. Это выражается не только в использовании данных вавилонских наблюдений, не только в усвоении шестидесятиричной системы счисления, но и в том, что в греческую науку проникают вычислительные методы вавилонян, основанные на операциях с линейными числовыми разностями. Будучи значительно более примитивными по сравнению с геометрическими методами греков, эти числовые методы сосуществуют рядом с ними, с течением времени находя все более широкое применение.

Влияние Вавилона выражается еще и в том, что к этому времени в античную науку проникает астрология, которая не была известна грекам классической эпохи, но которая издавна процветала в Междуречье. Особый успех астрология имеет у римлян, отличавшихся склонностью ко всякого рода суевериям и предрассудкам. При этом астрология в греко-римском мире приобретает существенно иные функции по сравнению с той ролью, какую она играла в странах Древнего Востока. Там наблюдения за такими небесными явлениями, как затмения, появления комет, необычные сочетания планет, имели целью предугадать счастливые или, чаще, пагубные события, предвестием которых эти явления считались. Такими событиями могли быть победа или поражение в войне, голод, наводнение, засуха и т. д. Теперь же динжение небесных светил стало связываться с индивидуальными судьбами людей. Основной и, в сущности, единственной задачей астрологии становится составление гороскопов, причем этим делом вынуждены заниматься самые крупные ученые. Более того, можно предполагать, что именно интерес к астрологии был важнейшим фактором, обусловившим новый подъем астрономической науки.