У реальному житті часто застосовуються знижки на обсяг замов-
лення (оптові знижки): чим більше розмір замовлення, тим мен-
шу ціну доводиться сплачувати за кожну одиницю. У такому ви-
падку для того, щоб визначити оптимальний розмір замовлення,
необхідно включити такі знижки в базову модель. Загальна вели-
чина витрат на матеріали містить у собі вартість самих матеріа-
лів, вартість зберігання запасів і вартість розміщення замовлень:
TC = C
D + C
0 q
q + CD,
h 2
(9.6)
де С — вихідна ціна одиниці матеріалу.
Якщо ціна одиниці матеріалу не залежить від розміру замов-
лення (тобто знижок немає), включення у формулу вартості са-
мих матеріалів не вплине на оптимальний розмір замовлення, а крива сумарних витрат зміститься вверх на постійну величину.
Якщо ж постачальник надає оптові знижки, ціна одиниці ма-
теріалу буде залежати від розміру замовлення, а у функції сумар-
них витрат з’являться точки розриву.
Паралельні криві витрат (по одній на кожен рівень цін) подані
на рис. 9.9. У точках, що відповідають мінімальному розміру за-
мовлення, для якого надається знижка, величина витрат «пере-
скакує» з однієї кривої на іншу. З графіка видно, що оптимальне
значення розміру може знаходитися або в мінімальній точці одні-
єї з кривих, або в одній із точок розриву, тому в умовах надання
оптових знижок послідовність аналізу така:
1. Визначити оптимальний розмір замовлення для кожного рі-
вня цін q 0 і, де і — індекс відповідної кривої.
2. Перевірити, чи попадають знайдені значення q 0 і в зону від-
повідного розміру знижки, тобто в зоні, де витрати описуються
кривою з індексом i.
3. Якщо деякий розмір замовлення q 0 і попадає в зону відпові-
дного розміру знижки (див. рис. 9.13, зона I), то він є найкращим
для даного рівня цін, якщо ж не попадає, то найкращим для дано-
го рівня цін буде розмір замовлення, що відповідає точці розри-
ву — qtі. Отже, якщо позначити оптимальне значення розміру за-
мовлення в зоні I як qt, то
qi = q 0 i, при _ q ∈ I;
qi = q Ii, при _ q ∉ I.
4. Розрахувати сумарні витрати на матеріали для кожного qt. Оптимальним буде такий розмір замовлення q, при якому сумар- ні витрати мінімальні.
Модель управління запасами при допустимому дефіциті. Якщо витрати на зберігання запасів вищі, ніж втрати, які викли- кані тимчасовою відсутністю запасів, то відсутність запасів на
складі протягом деякого невеликого проміжку часу може бути цілком допустимою. Тоді основну модель управління запасами необхідно перетворити з урахуванням допустимого рівня дефіци- ту. Тут можливі два варіанти розвитку подій:
1) попит, що виник у період відсутності запасів, відкладається аж до моменту, коли запаси на складі з’являться;
2) у період відсутності запасів на складі попит на них залиша-
ється незадоволеним.
У першому випадку максимальний розмір запасу на складі
менший від розміру замовлення на величину попиту, що виник
при відсутності запасів, а в другому випадку максимальний запас дорівнює розміру замовлення.
Розглянемо першу ситуацію.
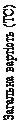Ціна 1
Ціна 2
Ціна 3
Розмір замовлення (q)
Рис. 9.13. Функція загальної вартості запасів при різних умовах надання оптових знижок:
I — знижка не надається; II — знижка 1; III — знижка 2
Критерієм ухвалення рішення щодо розміру замовлення, мак- симального рівня дефіциту в подібній ситуації також є мініміза- ція сумарних витрат підприємства. Рівняння сумарних витрат на запаси в ситуації можливого дефіциту доведеться модифікувати, включивши у нього вартість відсутності запасів.
Якщо позначити вартість відсутності одиниці запасу Сb, то формула набуде такого вигляду:
ТС = С 0 D / q + Chqcp + Сb scp, (9.7)
де qср — середній розмір запасу;
Scp — середній розмір дефіциту,
За період, поки запас на складі є (t 1), середній рівень запасу складає
(q – s) / 2. (9.8)
Таким чином, за весь цикл середній розмір запасу складе
q cp = (q – s) t 1 / (2 T). (9.9)
Тоді величину витрачання запасів за період t 1 (тобто D) можна обчислити за формулою:
D = (q – s) / t 1, (9.10)
D = q / T. (9.11)
Тому t 1 = (q – s) / D; Т = q / D. (9.12)
Шляхом підстановки значень t1 і Т у формулу середнього рів-
ня запасів одержуємо наступне:
(q − s) ⋅ (q − s) / D
2 q / D
(q − s)2
=
2 q
. (9.13)
Аналогічно можна знайти середній рівень дефіциту. Протягом часу t2 середній розмір дефіциту складе s /2, отже, середній дефі- цит за весь цикл Т складе:
s ⋅ t 2 /(2 T); (9.14) D = s / t 2; (9.15) t 2 = s / D; (9.16)
s = s ⋅ s / D
s. (9.17)
cp =
2 ⋅ q / D 2 q
Одержавши вирази для середнього дефіциту і середнього рів-
ня запасів, ми можемо написати рівняння сумарних витрат:
TC = C D / q + C
+ C.
(9.18)
0 h 2 q
b 2 q
Можна помітити, що сумарні витрати є функцією двох неза- лежних змінних: дефіциту s і розміру замовлення q. Тому для ви- значення оптимального розміру замовлення q і оптимальної ве- личини дефіциту s необхідно взяти дві часткові похідні: по q і по s і знайти такі q і s, при яких відповідні часткові похідні дорів- нюють нулю.
Оптимальний розмір замовлення в цьому випадку дорівнює:
q 2 = 2 C 0 D ⋅ Ch + Cb.
Ch Cb
(9.19)
Таким чином, оптимальний розмір замовлення в умовах припус- тимого дефіциту пропорційний оптимальному розміру замовлення при відсутності дефіциту, а коефіцієнт пропорційності залежить від витрат на зберігання і втрат, викликаних дефіцитом запасів:
q 2 = (q *)2 Ch + Cb,
C b
(9.20)
де q* — оптимальний розмір замовлення у випадку неприпусти-
мості дефіциту.
Оптимальний розмір дефіциту дорівнюватиме:
s = qCh.
Ch + Cb
(9.21)
Звідси випливає, що оптимальний розмір дефіциту залежить від розміру замовлення. Тому формулу можна перетворити, під- ставивши в неї значення q. Вийде такий вираз:
s 2 = 2 C 0 D ⋅
Cb
Ch.
Cb + Ch
(9.22)
А тепер повернемося до аналізу ситуації, при якій попит, що висувається до запасів у період дефіциту, не задовольняється вза- галі. Відмінність її від попередньої ситуації в тому, що максима- льний рівень запасу дорівнює розміру замовлення q. У рівнянні сумарних витрат, отриманому нами для попередньої ситуації, за- мінимо q на (q + s):
TC = C 0
D
q + s
+ Ch
q 2
2(q + s)
+ Cb
s 2
.
2(q + s)
(9.23)
Оптимальні значення q і s, як і в попередньому випадку, мож- на знайти, прирівнявши до нуля часткові похідні. Одержимо та- кий оптимальний розмір замовлення:
q 2 = 2 C 0 D ⋅ Ch + Cb = q 2* Ch + Cb
(9.24)
q Cb Cb
Оптимальний максимальний дефіцит складає:
s 2 = 2 C 0 D ⋅
Cb
Ch.
Cb + Ch
(9.25)
Резервний запас. Подана раніше модель управління запасами заснована на ряді припущень, що спрощують, зокрема, про те, що час постачання заздалегідь точно відомо і витрата запасів в оди- ницю часу завжди однаковий Однак на практиці ці припущення майже ніколи не виконуються: нерідкі зриви постачань, витрата запасів коливається залежно від випадкових факторів. Тому ви- никає необхідність у формуванні резервного запасу на випадок подібних «очікуваних несподіванок». Таким чином, в умовах не- визначеності рівень повторного замовлення перевищує рівень повторного замовлення в умовах визначеності на величину, рівну резервному запасу.
Резервний запас не тільки допомагає підприємству застраху- ватися від недостачі ресурсів, але і збільшує витрати збереження. Критерієм прийняття рішень у такій ситуації знову буде мінімі- зація сумарних витрат.
У даному випадку релевантними (значимими) будуть дні гру-
пи витрат:
• витрати, викликані недостачею запасів:
• витрати збереження резервного запасу.
Витрати на зберігання резервного запасу складають Сh R, де R — розмір резервного запасу. Сh — витрати на зберігання оди- ниці запасів.
Втрати, які викликані недостачею запасів, визначаються спе- цифікою конкретного підприємства, зокрема, вони складаються з таких складників:
• втраченого маржинального прибутку від реалізації продук-
ції, яку не вдалося виготовити і продати внаслідок відсутності
відповідних матеріалів;
• додаткових витрат на вимушене термінове придбання чи са-
мостійне виготовлення матеріалів;
• маржинального прибутку, який буде втрачено через зменшен-
ня частки ринку (відсутність необхідної продукції на складі приведе
до того, що покупці віддадуть перевагу продукції конкурента);
• витрат на зупинку і повторний запуск виробничого процесу
й ін.
Для визначення очікуваних втрат необхідно знати ймовірний
розподіл втрат, що залежить від ймовірного розподілу двох випа-
дкових величин: питомої витрати матеріалу за одиницю часу і
часу постачання.
Щоб знайти величину резервного запасу, необхідно визначити
ймовірність відсутності запасів на складі, яку можна вважати
прийнятною, тобто вибрати рівень обслуговування. Наприклад,
якщо допустима ймовірність відсутності запасів складає 6 %, то
рівень обслуговування складає 94 %. Рівень обслуговування ви-
значається виходячи зі значимості втрат фірми у разі відсутності
запасів: чим вагоміші втрати, тим більшим повинен бути рівень
обслуговування. Резервний запас визначають таким чином, щоб
ймовірність наявності запасів на складі була більшою від вибра-
ного рівня обслуговування.
Вищеописані критерії прийняття рішень вимагають викорис-
тання могутнього математичного апарата, зокрема застосування
методів лінійного програмування, яке за останні роки отримало
значне поширення.
