Такие уравнения приводятся к виду
. (4)
Для нахождения решения уравнения с разделяющимися переменными представим его в виде 
и проинтегрируем: 
. Решение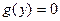 
является частным решением уравнения (4) и должно включаться в множество его решений.
Однородные дифференциальные уравнения
Функция 
называется однородной степени 
, если для любого числа 
имеет место тождество 
. Дифференциальное уравнение вида 
называется однородным, если функции и 
являются однородными одной степени. Однородное дифференциальное уравнение интегрируется заменой переменных 
.
Линейные дифференциальные уравнения
Такое уравнение может быть представлено в виде
. (5)
Его решение ищется в виде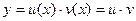 
, тогда по формуле производной произведения 
. После подстановки выражения для 
и 
в (5) получим 
, откуда 
. Далее предполагается, что выражение в скобках принимает значение, равное нулю, и уравнение (5) сводится к паре дифференциальных уравнений с разделяющимися переменными вида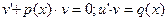 
.
Уравнения в полных дифференциалах
Если для дифференциального уравнения вида найдется функция 
, дифференциал которой совпадает с левой частью уравнения, т.е.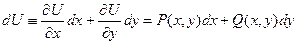 
, то уравнение называют уравнением в полных дифференциалах. Тогда 
, 
, а решение уравнения в неявном виде определяется как 
. При этом должно выполняться условие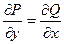 
, т.е. равенство смешанных производных второго порядка. Для определения вычисляют 
, откуда путем дифференцирования по определяют 
. Поскольку выражение в левой части есть , то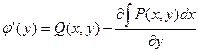 
. Интегрируя полученное равенство по получают 
, подстановка которого в дает решение исходного уравнения.
Дифференциальные уравнения старших порядков
Дифференциальные уравнения второго порядка, допускающие понижение порядка
Общий вид ОДУ, разрешенного относительно старшей производной, имеет вид
. (6)
Его общее решение имеет вид 
и содержит 2 независимые произвольные постоянные 
и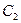 
. В общем случае ОДУ II порядка не может быть решено в конечном виде.
1) ОДУ (6) не содержит аргумента x, т.е.имеет вид 
, 
или 
.
В этом случае интегрирование производится путем замены переменной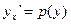 
. Тогда 
. При подстановке получаем:
а) уравнение принимает вид 
, т.е. сводится к ОДУ I порядка;
б) уравнение принимает вид 
или 
, т.е. представляет собой ОДУ I порядка с разделяющимися переменными;
в) уравнение принимает вид 
, откуда 
, т.е. также получается ОДУ I порядка с разделяющимися переменными.
2) ОДУ (6) не зависит от y, т.е. имеет вид 
. Тогда замена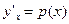 
, 
приводит к виду 
, т.е. получается ОДУ I порядка.
