Рулевой привод, представляющий собой систему тяг и рычагов, служит для передачи усилия от сошки на поворотные цапфы и осуществления заданной зависимости между углами поворота управляемых колес. При проектировании рулевых управлений выполняют кинетический и силовой расчет рулевого привода и прочностной расчет узлов и деталей рулевого управления.
Основной задачей кинематического расчета рулевого привода является определение углов поворота управляемых колес, нахождении передаточных чисел рулевого механизма, привода и управления в целом, выбор параметров рулевой трапеции и согласовании кинематики рулевого управления и подвески. Исходя из геометрии поворота троллейбуса (рис. 50) при условии, что управляемые передние колеса катятся без проскальзывания и их мгновенный центр поворота лежит на пересечении осей вращения всех колес наружный 
, и внутренний 
углы поворота колес связаны зависимостью:
, (4)
где 
- расстояние между точками пересечения осей шкворней с опорной поверхностью.
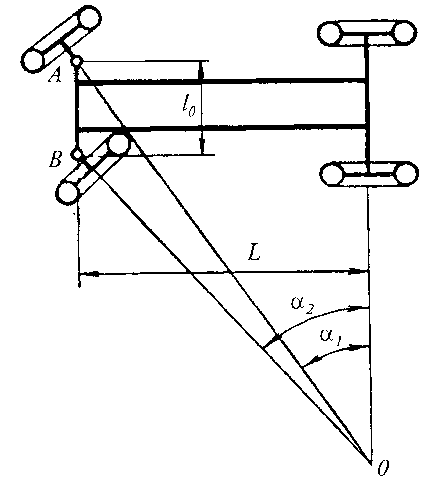
Рисунок 50. Схема поворота троллейбуса без учета боковой эластичности шин.
Из полученного выражения (4) следует, что разность котангенсов углов поворота внешнего и внутреннего управляемых колес должна быть всегда величиной постоянной, а мгновенный центр поворота троллейбуса (точка 0) должен лежать на продолжении неуправляемой оси.
Только при соблюдении этих теоретических условий вес колеса троллейбуса на повороте будут двигаться без скольжения, т.е. иметь чистое качение. От рулевой трапеции требуется, чтобы она обеспечивала вытекающие из геометрии поворота соотношения между углами поворота управляемых колес.
Параметрами рулевой трапеции являются шкворневая ширина (рис. 51), расстояние п между центрами шаровых шарниров рычагов трапеции; длина т и угол θ наклона рычагов поворотных цапф. Подбор параметров трапеции при жестких в боковом направлении управляемых колесах начинается с определения угла θ наклона рычагов трапеции. Они располагаются таким образом, чтобы а - (0.7...0.8,) L при заднем расположении поперечной тяги. Угол θ может быть найден для максимальных теоретических углов 
и 
по формуле:
или по графикам, приведенным на (рис.7б). Значение угла θ = 66...74°, а отношение длины рычагов к длине поперечной тяги т/п = 0.12....0.16. Длину m принимают возможно большей по условиям компоновки. Тогда
.
Рисунок 51. Схема рулевой трапеции и зависимость а/L от l0/L 1-3: при m/n равном соответственно 0,12; 0.14; 0,16
Общее кинематическое передаточное число рулевого управления, определяемое передаточными числами механизма Uм и привода Uпк равно отношению полного угла поворота рулевого колеса к углу поворота колеса от упора до упора
.
Для нормальной работы рулевого привода максимальное значение углов а, и а, находится в пределах 
. Для троллейбусов суммарное число оборотов рулевого колеса при повороте управляемых колес на 40о (± 20°) от нейтрального положения не должно превышать 3,5 (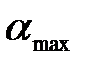
= 1260о) без учета угла свободного поворота рулевого колеса, что соответствует 
.
Схематическую компоновку рулевого привода выполняют для определения размеров и расположения в пространстве сошки, тяг и рычагов, а также передаточного числа привода. При этом стремятся обеспечить одновременную симметричность крайних положений сошки относительно ее нейтрального положения, а также равенство кинематических передаточных чисел привода при повороте колес как вправо, так и влево. Если углы между сошкой и продольной тягой, а также между тягой и поворотным рычагом в его крайнем положении приблизительно одинаковы, то эти условия выполняются.
В силовом расчете определяются усилия: необходимые для поворота управляемых колес на месте, развиваемые цилиндром усилителя; на рулевом колесе при работающем и неработающем усилителе; на рулевом колесе со стороны реактивных элементов распределителя; на колесах при торможении; на отдельных деталях рулевого управления.
Сила F, необходимая для поворота управляемых колес на горизонтальной поверхности троллейбуса, находится исходя из суммарного момента МΣ на цапфах управляемых колес:
,
где Мf –момент сопротивления перекатыванию управляемых колес при повороте вокруг шкворней; Мφ –момент сопротивления деформации шин и трения в контакте с опорной поверхностью в следствии проскальзывания шины; Мβ, Мφ –моменты обусловленные поперечным и продольным наклоном шкворней (рис. 8).
Рисунок 52. К расчету момента сопротивления повороту колеса.
Момент сопротивления перекатыванию управляемых колес при повороте вокруг шкворней определяется зависимостью:
,
где f – коэффициент сопротивления перекатыванию; G1 – осевая нагрузка передаваемая управляемыми колесами; 
– радиус обкатки колеса вокруг оси шкворня: 
=0.06...0.08 м; l –длина цапфы; r0 –расчетный радиус колеса; λ – угол развала колес; β – угол наклона шкворня.
Момент сопротивления деформации шин и трения в контакте с опорной поверхностью в следствии проскальзывания шины определяются зависимостью:
,
где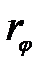 
– плечо силы трения скольжения относительно центра отпечатка шины.
Если принять, что давление по площади отпечатка распределяется равномерно,
,
где 
– свободный радиус колеса. В случае, когда 
.
При расчетах коэффициент сцепления с опорной поверхностью выбирают максимальным φ= 0.8.
Моменты, обусловленные поперечным и продольным наклоном шкворней, равны:
;
,
где 
- средний угол поворота колеса; 
; γ – угол наклона шкворня назад.
Усилие на ободе рулевого колеса
,
где 
– радиус рулевого колеса; η – КПД рулевого управления: η= 0.7…0.85.
Полученное значение 
сопоставляют с допустимым 
на рулевом колесе. Принимают 
. Если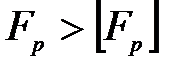 
, необходима установка усилителя.
