2)  , 0
, 0  .
.
Тема 8. Тригонометричні рівняння
Приклад 1. Розв`яжіть рівняння:
1) 

 ,
, 

Відповідь: 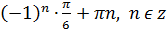
2) 





 (
( 1)
1) 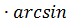




Відповідь: 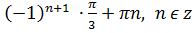
3) 





Відповідь: 
4) 


 -
- 

 ±(
±(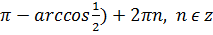

 ±(
±( +2
+2 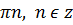 ;
; 
Відповідь: 
5) 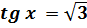




Відповідь: 
6) 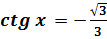

 -
-  +
+ 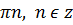






Відповідь: 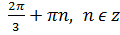
7) 

 , оскільки
, оскільки 
Відповідь: коренів не має
8) 
 , оскільки
, оскільки 
Відповідь: коренів не має
9)  +1=0
+1=0


 (
(
 )
) 


Відповідь: 
10) 
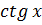 =
= 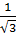
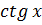 =
= 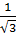
 =
= 

 =
= 
Відповідь: 
11) 
2 
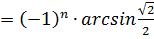 +
+ 


Відповідь: 
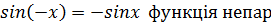 на на
|
| Зверніть увагу! |

 +2
+2 
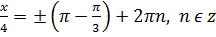
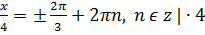

Відповідь: 
13) 

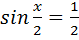



Відповідь: 
Зверніть увагу!
 ( (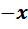 ) )  функція парна функція парна
|

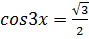


Відповідь:
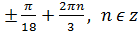
Зверніть увагу! a =( 3=( 3=(
|
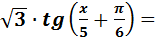 3
3 
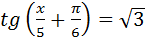




Відповідь: 
Приклад 2.
Розв’яжіть рівняння
 Дане рівняння є квадратним відносно
Дане рівняння є квадратним відносно  . Зробимо заміну змінної, а саме:
. Зробимо заміну змінної, а саме: 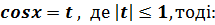

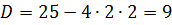
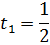
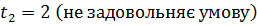

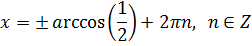

Відповідь: 
Приклад 3.
Зверніть увагу!

|
Розв’язати рівняння:
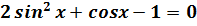
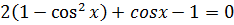


 :
: 
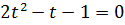








Відповідь: 
Приклад 4. Розв’язати рівняння:
Зверніть увагу!

|

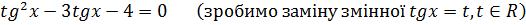

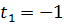

П 




Відповідь: 
 де
де  числа, називається однорідним рівнянням І степеня.
числа, називається однорідним рівнянням І степеня.
Метод розв’язання: ділення обох частин рівняння на 
Приклад 5. Розв’язати рівняння:






 Відповідь:
Відповідь: 
Рівняння виду, де а,, с – числа, називається однорідним рівнянням ІІ степеня.
Метод розв’язання: ділення обох частин рівняння на 
Приклад 6. Розв’язати рівняння:
 однорідне рівняння ІІ степеня.
однорідне рівняння ІІ степеня.
Поділимо ліву частину на праву частину на 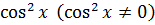
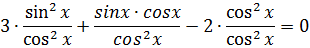
 . Зробимо заміну змінної:
. Зробимо заміну змінної: 
Маємо: 



Повертаючись до заміни, маємо:
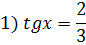



Відповідь: 
Приклад 7.
Зверніть увагу!

|
Розв’язати рівнння:









Зробимо заміну змінної:

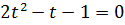


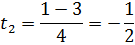
Повертаючись до заміни, маємо:

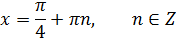


Відповідь: 
Приклад 8.
Розв’язати рівняння:



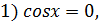 тоді
тоді 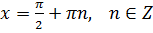






Відповідь: 
Зверніть увагу!

|
Приклад 9.
Розв`язати рівняння:








Зверніть увагу!

|
Приклад 10.
Розв`язати рівняння:




 (не має розв'язків)
(не має розв'язків)
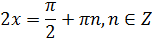
 Відповідь
Відповідь 
1) 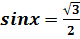 ;2) ;2)  ;3) ;3) 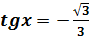 ;4) ;4)  ;5) ;5)  ;6) ;6)  ;7) ;7)  ;8) ;8) 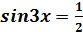 ;9) ;9)  ;10) ;10) 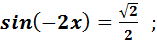 11) 11)  ;12) ;12)  ;13) ;13) 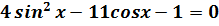 ; ;
| 14)  ;
15) ;
15) 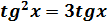 ;
16) ;
16)  ;
17) ;
17)  ;
18) ;
18)  ;
19) ;
19)  ;
20) ;
20) 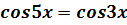 . .
|
Вправи для самостійного розв’язування до теми 8:
Тема 9. Похідна функції
1. Поняття приросту аргументу і приросту функції в точці 
Нехай задана функція  . Зафіксуємо деяку точку
. Зафіксуємо деяку точку  з області визначення функції
з області визначення функції 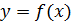 . Приростом аргументу (позначається
. Приростом аргументу (позначається  , читається «дельта ікс») називається різниця
, читається «дельта ікс») називається різниця  , тобто
, тобто 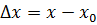 . Звідси
. Звідси  .
.
Різницю  – називають приростом функції.
– називають приростом функції.
2. Означення похідної:
Похідною функції 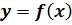 , у точці
, у точці  називається границя відношення приросту функції в точці
називається границя відношення приросту функції в точці  до приросту аргументу, коли приріст аргументу прямує до нуля:
до приросту аргументу, коли приріст аргументу прямує до нуля:

3. Геометричний зміст похідної:
 Значення похідної функції
Значення похідної функції  в точці
в точці  дорівнює тангенсу кута нахилу дотичної до графіка функції в точці з абсцисою
дорівнює тангенсу кута нахилу дотичної до графіка функції в точці з абсцисою  та дорівнює кутовому коефіцієнту цієї дотичної. Отже,
та дорівнює кутовому коефіцієнту цієї дотичної. Отже, 
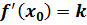
 – кутовий коефіцієнт дотичної.
– кутовий коефіцієнт дотичної.
4.
 у точці з абсцисою
у точці з абсцисою  :
:

5. Механічний зміст похідної:
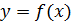 у точці
у точці 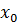 виражає швидкість зміни функції або процесу, який ця функція описує у цій точці. Отже, якщо функція
виражає швидкість зміни функції або процесу, який ця функція описує у цій точці. Отже, якщо функція  описує рух матеріальної точки, тобто залежність пройденої відстані
описує рух матеріальної точки, тобто залежність пройденої відстані  від часу
від часу  , то її похідна задає залежність швидкості
, то її похідна задає залежність швидкості  матеріальної точки від часу
матеріальної точки від часу  .
.


6. Правила диференціювання:
1)
| Обов`язково запам`ятайте!!! |
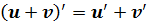
2) 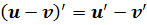
3) 
4) 
C -число
7. Похідна складеної функції: 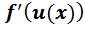 =
= 
Таблиця похідних
1) 

 const 12)
const 12)  23)
23) 
2)  13)
13)  24)
24) 
3)  ;
; 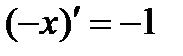 14)
14)  25)
25) 
4)  15)
15)  26)
26) 
5)  16)
16)  27)
27) 
6) 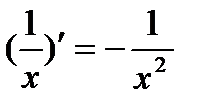 17)
17)  28)
28) 
7) 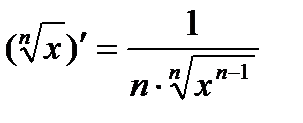 18)
18)  29)
29) 
8)  19)
19)  30)
30) 
9)  20)
20)  31)
31) 
10)  21)
21) 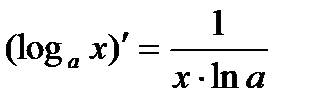 32)
32) 
11)  22)
22)  33)
33) 
Приклад 1. Знайдіть похідну функцій:
1)  ;
;



2)  ;
;

3) 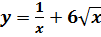 ;
;

4)  . Оскільки
. Оскільки 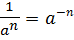 ,тоді
,тоді



5) 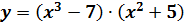



6) 



7)  ;
;


 :
:
8) 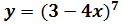 Зверніть увагу
Зверніть увагу 


Зверніть увагу 

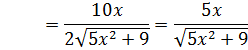
10) Знайти похідну складеної тригонометричної функції:



11) Знайти похідну складеної тригонометричної функції:

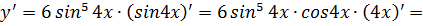

12) Знайти похідну функції: Зверніть увагу 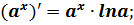

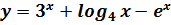 ;
;
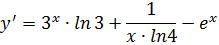
13) Знайти похідну складеної функції:
Зверніть увагу 
|




14) Знайти швидкість та прискорення точки, що рухається за законом:



15) Скласти рівняння дотичної до графіка функції:

Запам`ятай!

|
1) 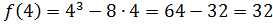
2) 
3) 
4) 
Вправи для самостійного розв’язування до теми 9:
1. Знайдіть похідну функції:
1)  = 7
= 7  4 – 5
4 – 5  3 – 4
3 – 4  + 6; 4)
+ 6; 4) 
 ;
;
2)  =
=  –
– 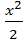 +
+ 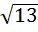 ; 5)
; 5) 


 5
5  ;
;
3) 
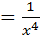 –
–  ; 6)
; 6)  8
8 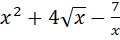 +9;
+9;
7)  ; 18
; 18 
8) 




 ; 19)
; 19) 
9)  =
= 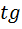 (
( +
+  ) +
) +  (2
(2  –
–  ); 20)
); 20) 
10)  = (
= ( 2 – 4) (
2 – 4) ( 3 + 1); 21
3 + 1); 21 
11)  =
=  ; 22)
; 22) 
12)  = (5
= (5  + 4)10; 23
+ 4)10; 23 
13)  =
=  ; 24)
; 24)  +
+  ;
;
14)  =
=  3
3  ; 25
; 25 
15)  =
= 
 ; 26
; 26  ;
;
16)  =
= 
 ; 27
; 27 
17)  =
=  4 7
4 7  ; 28)
; 28)  .
.
2.Обчисліть значення похідної функції  у точці
у точці 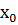 , якщо
, якщо
 ,
,  = 4
= 4 
2) 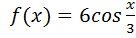 ,
,  =
= 
2. 1)Складіть рівняння дотичної до графіка функції  (
( ) =
) =  2 – 4
2 – 4
у точці  = 2
= 2
2)Складіть рівняння дотичної до графіка функції  (
( ) =
) = 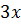 2 – 4
2 – 4 
у точці  =
= 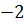
3. Точка рухається за законом:
 Знайдіть миттєву швидкість точки у момент
Знайдіть миттєву швидкість точки у момент  .
.
Тема 10. Застосування похідної до дослідження функції
1. Дослідження функції на монотонність:
Якщо для функції  її похідна
її похідна  додатна у кожній точці проміжку
додатна у кожній точці проміжку  , тобто
, тобто 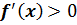 , то функція
, то функція  зростає на цьому проміжку.
зростає на цьому проміжку.
Якщо  на проміжку
на проміжку  ,то функції
,то функції  спадає на проміжку
спадає на проміжку 
Проміжки зростання та спадання функції називають проміжками монотонності.
2. Критичні точки: внутрішні точки області визначення, у яких похідна функції дорівнює нулю або не існує.
3. Точки екстремуму (точки максимуму та точки мінімуму).
Достатня умова екстремуму
Нехай  - критична точка.
- критична точка.
Якщо функція 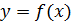 неперервна в точці
неперервна в точці  і похідна
і похідна  змінює знак при переході через точку
змінює знак при переході через точку  , зліва направо, то
, зліва направо, то  – точка екстремуму функції
– точка екстремуму функції  .
.
Якщо при переході через  похідна
похідна 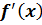 змінює знак з «
змінює знак з « 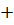 » на «
» на «  », то
», то

|
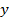
|
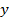
|
 – точка максимуму.
– точка максимуму.

|
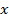
|

|

|
Знак 
|
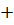
|

|
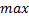
|

|
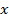
|
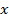
|

|
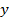
|
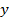
|
 похідна
похідна  змінює знак з
змінює знак з  на
на  , то
, то  – точка мінімуму.
– точка мінімуму.
Знак 
|

|

|
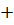
|

|

|

|
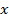
|
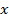
|
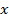
|

|
Якщо при переході через критичну точку зліва направо знак похідної не змінюється, то ця критична точка не є точкою екстремуму.
Екстремумами функції називають значення функції в точках екстремуму.
4. Схема дослідження функції  на монотонність та екстремуми
на монотонність та екстремуми
1) Знайти область визначення функції.
2) Знайти похідну 
3) Знайти критичні точки.
4) Позначити критичні точки на області визначення, знайти знак похідної та поведінку функції на кожному з інтервалів, на які розбивається область визначення.
5) Визначити для кожної критичної точки, чи є вона точкою максимуму або мінімуму, чи вона не є точкою екстремуму.
6) Записати результати дослідження (проміжки монотонності та екстремуми).
5. Схема знаходження найбільшого та найменшого значення функції на відрізку  :
:
1) Знайти область визначення функції.
2) Знайти похідну  .
.
3) Знайти критичні точки.
4) Вибрати критичні точки, які належать заданому відрізку  .
.
5) Обчислити значення функції в критичних точках і на кінцях відрізка
 .
.
6) Порівняти одержані значення функції й вибрати з них найбільше та
найменше.
6. Схема дослідження функції для побудови її графіка:
1) Знайти область визначення функції.
2) Дослідити на парність (непарність), періодичність.
3) Знайти точки перетину графіка з осями координат.
4) Знайти похідну  .
.
5) Знайти критичні точки.
6) Знайти проміжки монотонності.
7) Знайти точки екстремуму та значення функції в цих точках.
8) Побудувати графік функції.
Приклад 1.
Знайти критичні точки функції:
 =
= 
 3 +
3 + 
 2 –
2 –  + 7.
+ 7.
1. Знайдемо область визначення функції:

2. Знайдемо похідну 
 =
= 
 3
3  2 +
2 +






