Якщо 
| Якщо 
| |
 , тоді , тоді
 знак нерівності зберігається
знак нерівності зберігається
|  , тоді , тоді
 знак нерівності змінюється на протилежний
знак нерівності змінюється на протилежний
| |
Якщо 
| Якщо 
| |
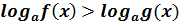 , тоді , тоді
 знак нерівності зберігається
знак нерівності зберігається
|  , тоді , тоді
 знак нерівності змінюється на протилежний
знак нерівності змінюється на протилежний
|
Приклад 1
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 




Враховуючи ОДЗ, маємо:

|
 (16;
(16; 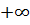 ) 0 16
) 0 16
Відповідь:  (16;
(16; 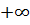 )
)
Приклад 2
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 



br DfA844/+/A8AAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAA AAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAA AAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQBIvtemAwIAAC0EAAAOAAAAAAAA AAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQBjVsUG3AAAAAcBAAAPAAAA AAAAAAAAAAAAAF0EAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAZgUAAAAA " strokecolor="black [3213]"/>

|
Враховуючи ОДЗ, маємо:

|
0 4
Відповідь: 
Приклад 3
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 


Враховуючи властивість логарифмічної функції, маємо:



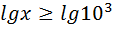

З врахуванням ОДЗ, маємо:

|
0 1000
Відповідь: 
Приклад 4
Розв’язати нерівність:
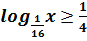 ОДЗ:
ОДЗ: 






|

Враховуючи ОДЗ, маємо:

|

Відповідь: 
Приклад 5
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 

 1
1

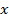
|
| -1 |

Відповідь:  (0;
(0; 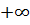 )
)
Приклад 6
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 

 2
2

| -1 |
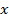
|

Відповідь:  (1;
(1; 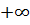 )
)
Приклад 7
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 

 2
2
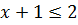
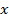
|
| -1 |

Враховуючи ОДЗ, маємо:
 є (-1;1]
є (-1;1]
Відповідь:  є (-1;1]
є (-1;1]
Приклад 8
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 





|
 -658
-658
Відповідь: 
Приклад 9
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 

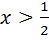




|
Враховуючи ОДЗ, маємо:

|
 2
2
Відповідь: 
Приклад 10
Розв’язати нерівність:



|

|

|


Відповідь: 
Приклад 11
Розв’язати нерівність:


 ;
; 

|

|
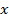
|
Відповідь: 
Приклад 12
Розв’язати нерівність:
 ОДЗ:
ОДЗ: 
Зробимо заміну замінної:

Одержимо:

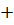
|
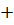
|

|

|
| t |


Повертаючись до заміни, маємо:



Враховуючи ОДЗ, маємо:

|

|

|

|

Приклад 13
Розв’язати нерівність:
2 
Зробимо заміну змінної:
 ,
, 
Одержимо:

Розв’яжемо методом інтервалів:



|
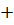
|
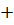
|


|

|

|

Маємо:
 ;
;  ;
;  ;
;
 ;
;  ;
;
 ;
; 
Враховуючи ОДЗ, маємо:
Відповідь: 
Вправи для самостійного розв’язування до теми 6:
Розв’яжіть нерівність: 1)  10)
10) 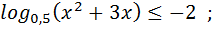 2)
2)  11)
11) 
3)  ; 12)
; 12)  ; 4)
; 4)  ; 13)
; 13) 
5)  ; 14)
; 14) 
6)  ; 15)
; 15)  ;
;
7)  ; 16)
; 16)  8)
8)  ; 17)
; 17) 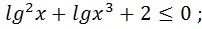
9)  ; 18)
; 18) 

Тема 7. Тригонометричні перетворення
Радіанна і градусна міра кутів  =
= 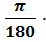
 (радіан)
(радіан)
 =
= 

 (градусів)
(градусів)
Наприклад:  =
= 
 30 =
30 =  (рад)
(рад)
 =
= 

 =
= 
Графіки тригонометричних функцій








Приклад 1 Зверніть увагу!
Спростити вираз: Завдання на використання основних
тригонометричних формул
1) 1 


 =
= 

 = 0
= 0
2) (1  ) (1
) (1  )= 1
)= 1 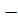
 =
= 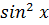
3)  =
= 

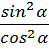 = 1
= 1
4) 
Приклад 2
Дано: 1) 
 =
=  0,8
0,8 


Знайти: 
 Враховуючи, що
Враховуючи, що 
 , тобто
, тобто 
 2)
2) 
 3)
3) 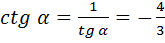
Відповідь: 
Приклад 3 Зверніть увагу!


Знайти значення виразу: 
1) 
2) 
3) 
4) 
5) 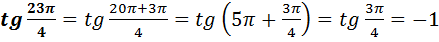
6) 

Приклад 4
Скоротіть дріб:
1) 
2) 
3) 
4) 


Приклад 5
Спростіть вираз: Зверніть увагу!
1)  Завдання на формули зведення
Завдання на формули зведення
2) 
| Зверніть увагу! Завдання на використання формул 3 двійок |
Спростіть вираз:
1) 
2)  2
2 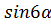
Приклад 7 Зверніть увагу!
Спростіть вираз:Для розв`язання треба використовувати
формули додавання
1) 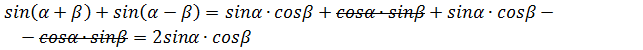
2) 

Приклад 8
Спростіть вираз:
1)  6
6 
2)  23
23 
Приклад 9
1)  10
10 
Зверніть увагу!
Для розв`язання треба використовувати формули
перетворення суми і різниці тригонометричних функцій у добуток.
2) 
3) 
Вправи для самостійного розв’язування до теми 7:
1. Спростити вираз:
1)  ; 5)
; 5) 
2)  ; 6)
; 6) 
3)  ; 7)
; 7)  ;
;
4) 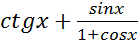 ; 8)
; 8) 
2. Знайдіть значення виразу:
 ;
;
2) 
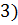
 .
.
3. Зведіть до тригонометричної функції кута 
 ; 2) cos
; 2) cos 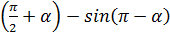
4. Розкладіть на множники:
1)  ; 3)
; 3)  ;
;
2) cos40  ; 4)
; 4)  .
.
5. Спростіть вираз:
1)  ; 4)
; 4)  ;
;
2)  ; 5)
; 5)  ;
;
3) cos3  6)
6) 






