 з раціональним показником
з раціональним показником 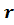 , представленим у вигляді
, представленим у вигляді 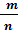 , де
, де 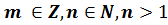 називається число
називається число 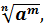 тобто
тобто
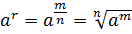
Приклад: 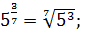

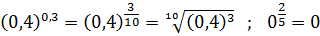
Функція виду 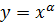 , де
, де 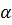 – будь-яке дійсне число, називається степеневою функцією.
– будь-яке дійсне число, називається степеневою функцією.




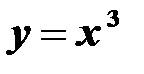 ,
, 
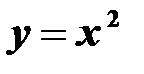 ,
, 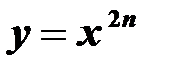


 ,
, 
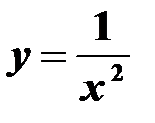 ,
, 


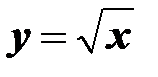 ,
, 
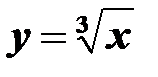 ,
, 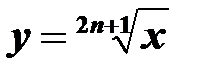
Приклад 5. Спростіть дріб:
Зверніть увагу!
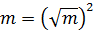
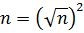
| Зверніть увагу!

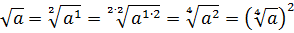
|
1) 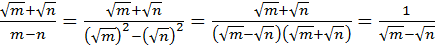 ;
;
2) 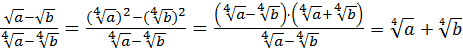 .
.
Приклад 6. Спростіть дріб:
Зверніть увагу!

| Зверніть увагу!
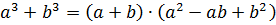
|
1) 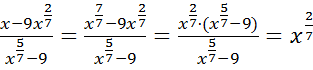 ;
;
2) 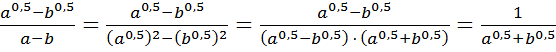 ;
;
3) 
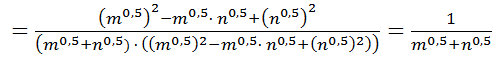
Приклад 7. Знайдіть область визначення функції:
1) 
2) 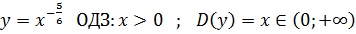
3) 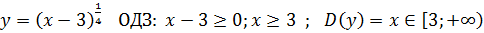
4) 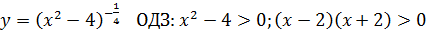
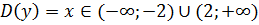
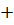
|
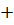
|
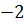
|

|

|
Приклад 8. Знайдіть область визначення функції:
1) 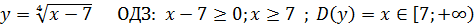
2) 
3) 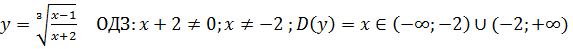
Вправи для самостійного розв’язування до теми 1:
1. Знайдіть значення виразу:
1) 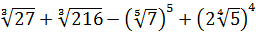 ;
;
2)  ;
;
3) 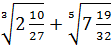 ;
;
4) 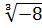 +
+ 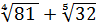 ;
;
5) 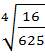 +
+ 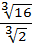 .
.
2. Спростіть вираз:
1) 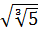 ; 2)
; 2) 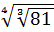 ; 3)
; 3) 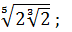 4)
4) 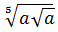 ; 5)
; 5)  .
.
3. Знайдіть область визначення функції:
1) 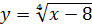 ; 5) y =
; 5) y = 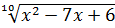 ;
;
2) 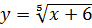 ; 6) y =
; 6) y = 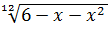 ;
;
3) 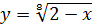 ; 7) y =
; 7) y = 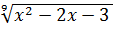 ;
;
4) 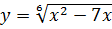 ; 8) y =
; 8) y =  .
.
4. Розв’яжіть рівняння:
1)  ; 5)
; 5) 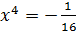 ;
;
2)  ; 6)
; 6) 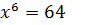 ;
;
3) 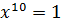 ; 7)
; 7) 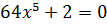 ;
;
4)  ; 8)
; 8) 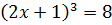 .
.
5. Винесіть множник з-під знака кореня:
1) 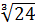 ; 4)
; 4)  ;
;
2)  ; 5)
; 5) 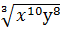 ;
;
3) 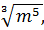
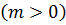 ; 6)
; 6) 
6. Внесіть множник під знак кореня:
1)  ; 2)
; 2) 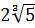 ; 3) 3
; 3) 3  ; 4)
; 4)  .
.
7. Скоротіть дріб:
1) 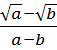 ; 6)
; 6) 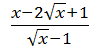 ;
;
2) 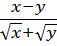 ; 7)
; 7) 

3)  ; 8)
; 8) 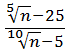
4) 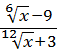 ;
;
5) 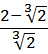 .
.
8. Знайдіть значення виразу:
1) 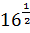 ; 2)
; 2) 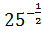 ; 3)
; 3) 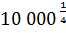 ; 4)
; 4) 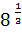 .
.
9. Знайдіть область визначення функції:
1) 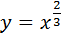 ; 2)
; 2) 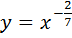 ; 3)
; 3)  ; 4)
; 4) 
10. Знайдіть значення виразу:
1) 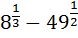 ; 2)
; 2) 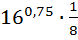 ; 3)
; 3)  ;
;
4) 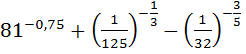 .
.
11. Знайдіт значення виразу:
1)  ; 2)
; 2) 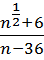 ; 3)
; 3) 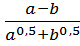 ;
;
4) 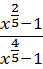 ; 5)
; 5) 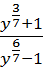 ; 6)
; 6) 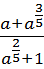 .
.
Тема 2. Ірраціональні рівняння.
Ірраціональними називають такі рівняння, у яких змінна міститься під знаком кореня. Найчастіше розв’язування ірраціональних рівнянь грунтується на зведенні заданого рівняння за допомогою деяких перетворень до раціонального рівняння. Як правило, це досягається за допомогою піднесення обох частин ірраціонального рівняння до одного і того самого степеня.
Розв’яжіть рівняння:
1) 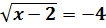
Оскільки  а
а 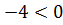 , то рівняння коренів не має.
, то рівняння коренів не має.
2) 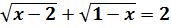 З найдемо ОД З:
З найдемо ОД З:

|
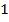
|
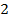
|

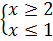 Система розв`язків не має
Система розв`язків не має
Відповідь: рівняння коренів не має
3) 
Обидві частини рівняння піднесемо до квадрату
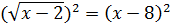 ;
;
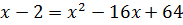 ;
;
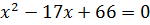 ;
;
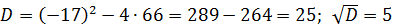

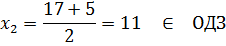
Зробимо перевірку:
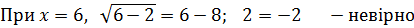
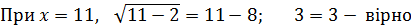
Відповід ь: 11
4) 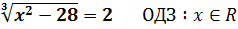
Обидві частини рівняння піднесемо до 3 степеня:
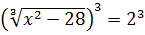
Маємо:
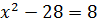


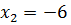
Відповід ь: 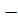 6 та 6.
6 та 6.
5) 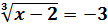
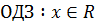
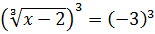
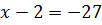

Відповідь:  25
25
6) 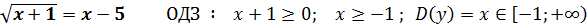
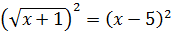
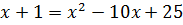
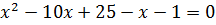

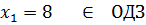

Зробимо перевірку:
При 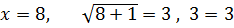
При 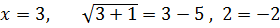 невірно
невірно
Відповідь: 8
7) 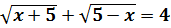
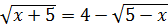
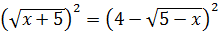

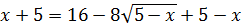
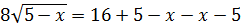
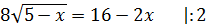
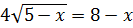
Обидві частини рівняння піднесемо до степеня 2:
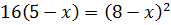

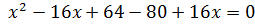
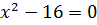
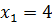

Зробимо перевірку:
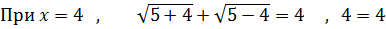
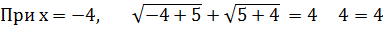
Відповідь: 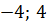
Вправи для самостійного розв’язування до теми 2:
Розв’яжіть рівняння:
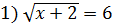 ; 2)
; 2) 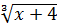 =2;
=2; 
4) 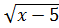 = x
= x  ;
; 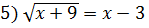 ;
;
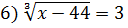 ;
;
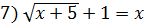 ;
;

9) 
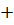
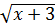
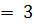 ;
;
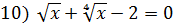 ;
;
11) 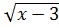
 2
2 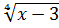 = 3;
= 3;
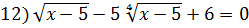 ;
;
 ;
;
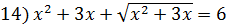 ;
;
 ;
;
 ;
;
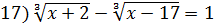 .
.
Тема 3. Показникова функція. Показникові рівняння.
Функція виду, де, називається показниковою функцією.
При 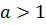
| При 
|
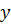 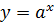 1
0
1
0 
|
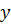 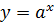 0
0 
|
| функція зростає | функція спадає |
1) 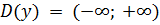
2) 
3) 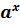 > 0 завжди
> 0 завжди
Приклад
Побудуйте графіки функцій:
1) 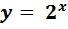
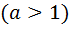 2 )
2 ) 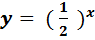
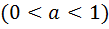

| -2 | -1 | |||
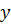
| 
| 
|

| -2 | -1 | |||
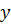
| 
| 
|
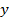
|
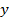
|
|
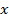
|
|
|
|
|
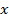
|
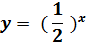
|
|
|
|
|
Рівняння виду, де, називають найпростішим показниковим рівнянням.
Основні методи розв`язання показникових рівнянь:






