Работа по перемещению проводника и контура
С током в магнитном поле
На движущиеся в проводнике носители тока со стороны магнитного поля действуют магнитные силы. Геометрическая сумма этих сил и обусловливает воздействие магнитного поля на проводник с током. Найдем эту силу.
Рассмотрим элемент проводника длиной dl и площадью поперечного сечения S, находящийся в магнитном поле с ин- дукцией 
. Если концентрация носителей тока в проводнике n, а их средняя скорость упорядоченного движения 
, то сила действующая на элемент тока dl, определяется следую- щим образом:
. (1.30)
Учитывая, что 
, а 
, получим
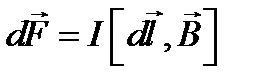, (1.31)
где dl – вектор, направленный по току.
Направление силы 
можно определить по правилу векторного произведения, либо по правилу левой руки.
Данная формула выражает закон Ампера, а силы, действующие на токи в магнитном поле, называют силами Ампера. Интегрируя (1.31) по линии тока, можно найти магнитную силу, действующую на тот или иной проводник в целом. В частности, для однородного поля 
и прямолиней- ного проводника длиной l с током I, сила Ампера равна
, (1.32)
где α - угол между направлением тока и вектора 
.
Выражение (1.32) позволяет также установить физический смысл и единицу измерения силовой характеристики магнитного поля. Если α = π/2, то
, (Тесла)
т.е. индукция 
численно равнасиле, действующей на единицу длины проводника, по которому течет единичный ток и который расположен перпендикулярно направлению однородного магнитного поля.
I
 
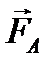l
|
| d x |
| ξ |
| Рис.1.8 |
Учитывая, что 
, получим
,
или после интегрирования
. (1.33)
Работа, совершаемая при перемещении проводника с током в магнитном поле, равна произведению силы тока на магнитный поток сквозь поверхность, охватываемую проводником при его движении.
Найдём работу, совершаемую над замкнутым контуром. Предположим, что контур, перемещаясь, остаётся в одной плоскости (рис.1.9). Разобьём контур на два участка 1-2 и 2-1. Силы приложенные к участку 1-2, образуют с направлением перемещения острые углы, поэтому работа А1>0.
где Ф0 и ФК – потоки магнитной индукции, пересекаемые участком 1-2 при его движении.
1 dФ
Ф0
I
Фн 
2
dF
|
| Фк I |
| Рис.1.9. ZХA |
Работа, совершаемая над участком 2-1 отрицательная, так как силы с направлением перемещения участка образуют тупые углы
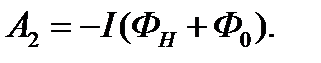
Работа, совершаемая над всем контуром, равна
.
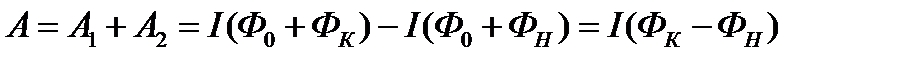Разность магнитного потока в конце перемещения ФК и в начале перемещения ФН дает приращение потока ΔФ через замкнутый контур. Таким образом
(1.34)
Эта формула справедлива при любом движении контура в произвольном магнитном поле.
Магнитное поле оказывает ориентирующее действие на замкнутый проводящий контур, по которому идет постоянный
ток. Найдем выражение для момента сил, действующих в однородном магнитном поле на плоский прямоугольный контур с током (рис.1.10).
Силы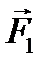 
и 
, приложенные к проводникам 1-2 и 3-4, численно равны и направлены в противоположные стороны, поэтому они создают пару сил, вращательный момент которой
,
где S = ab - площадь контура.
| Рис.1.10 |
Учитывая, что IS = Pм, получим
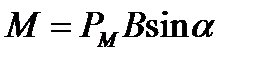, (1.35)
или в векторной форме
. (1.36)
Таким образом, магнитное поле стремится повернуть контур с током так, чтобы его магнитный момент 
сориентировался в направлении вектора 
.
| Рис.2.8 |
и увеличился на dα, нужно совершить работу против сил поля, равную
. (1.37)
Работа внешних сил идет на увеличение потенциальной энергии контура
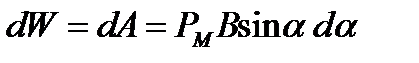. (1.38)
Интегрируя (1.38) по углу поворота и полагая константу интегрирования равной нулю, будем иметь
. (1.39)
Из полученной формулы видно, что минимум потенциаль- ной энергии достигается в положении устойчивого равновесия, когда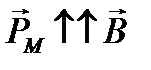 
.
1.5. Магнитное поле в веществе
1.5.1. Намагничивание вещества. Вектор намагниченности. Теорема Гаусса и теорема о циркуляции вектора 
для магнитного поля в веществе
Любое вещество под действием внешнего магнитного поля намагничивается, т. е. создает свое собственное поле. Для объяснения намагничивания Ампер предположил, что в веще- стве циркулируют круговые микротоки. Современные представления о строении вещества позволяют связать гипоте- тические токи Ампера с движением электронов в атомах или молекулах, а следовательно, с существованием молекулярных токов, обладающих магнитными моментами 
.
При отсутствии внешнего магнитного поля магнитные моменты отдельных атомов ориентированы хаотически, поэто-
му средний суммарный магнитный момент образца равен нулю. Если же все вещество поместить во внешнее магнитное поле, то молекулярные токи будут располагаться так, что их магнитные моменты будут преимущественно ориентированы в направлении намагничивающего поля. В результате весь образец приобретает отличный от нуля суммарный магнитный момент.
Для количественной характеристики степени намагничи- вания вещества вводится вектор намагниченности 
, определяемый выражением
, (1.40)
где 
- физически бесконечно малый объем; 
- магнитный момент отдельной молекулы.
Суммирование проводится по всем молекулам в объеме .
Намагниченность численно равна магнитному моменту единицы объема магнетика, поэтому может быть представ- лена в виде
, (1.41)
где n – концентрация молекул; 
- средний магнитный момент одной молекулы.
В результате намагничивания вещества в нем появляется собственное магнитное поле 
, связанное с вектором 
соотношением
. (1.42)
Наложение внешнего поля 
и собственного поля вещества 
образует результирующее поле
. (1.43)
Линии вектора 
и при наличии вещества остаются непрерывными, поэтому для результирующего магнитного поля теорема Гаусса имеет тот же вид, что и для поля в вакууме, т.е.
. (1.44)
Циркуляция вектора 
суммарного магнитного поля в магнетике определяется не только макротоками проводимости, но и молекулярными токами, охватываемыми контуром
. (1.45)
Сумма молекулярных токов может быть выражена через вектор намагничивания
. (1.46)
С учетом этого, циркуляция вектора 
(1.43) приводится к виду
. (1.47)
Введя новую вспомогательную характеристику магнитного поля, называемуюнапряженностью и равную
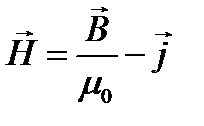, (1.48)
получим окончательно
. (1.49)
Таким образом, циркуляция вектора напряженности магнитного поля по произвольному контуру равна алгебраи- ческой сумме токов проводимости, охватываемых этим контуром. Уравнение (1.49) называется теоремой о циркуляции вектора 
или законом полного тока. Из этого уравнения следует, что единицей H является ампер, делённый на метр ([ H ] = А/м).
В однородной изотропной среде векторы 
и 
связаны простым соотношением
, (1.50)
где c (хи) – магнитная восприимчивость среды. Подставляя (1.50) в формулу (1.48), получим
или 
, (1.51)
где m = 1 + c - магнитная проницаемость среды.
Вектор 
является аналогом электрического смещения 
. Его введение во многих случаях значительно упрощает расчеты поля в магнетиках, поскольку напряженность поля в веществе 
совпадает с напряженностью внешнего поля 
, тогда как индукция результирующего поля равна
. (1.52)
Магнитная проницаемость m, следовательно, показы- вает, во сколько раз магнетик усиливает внешнее поле.
В зависимости от величины магнитной проницаемости и знака магнитной восприимчивости все магнетики подразделя- ются на:
1) диамагнетики, у которых c < 0 и m < 1;
2) парамагнетики, у которых c > 0 и m > 1;
3) ферромагнетики, у которых 
.
1.5.2. Магнитные моменты электрона и атома.
Атом в магнитном поле
Для того чтобы более детально разобраться с природой намагничивания и объяснить существование различных видов
магнетиков, необходимо обратиться к внутреннему строению вещества и рассмотреть магнитные свойства атомов и особен- ности их поведения в магнитном поле.
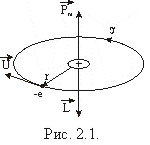
| Рис.1.11 |
(рис.1.11), образует круговой ток
. (1.53)
Орбитальному току соответ- ствует орбитальный магнит- ный момент электрона
. (1.54)
Движущийся по орбите электрон обладает также моментом импульса или орбитальным механическим моментом
. (1.55)
Поскольку направления скорости электрона и орбиталь- ного тока, вызванного его движением, противоположны, то противоположны также и направления векторов 
и 
(рис.1.11).
| Рис.3.1 |
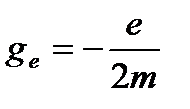. (1.56)
| Рис.1.9 |
Кроме орбитальных моментов и , электрон обладает ещё собственным механическим моментом LS, получив -шим название спина, и связанного с ним собственным магнитным моментом Pms, гиромагнитное отношение которых в два раза больше орбитального
. (1.57)
Установлено, что для электрона
и (1.58)
, (1.59)
где 
, 
- магнетон Бора, представляющий естественную единицу магнитного момента.
Результирующий магнитный момент атома или молекулы вещества равен векторной сумме орбитальных и спиновых магнитных моментов электрона
. (1.60)
Измерения магнитных моментов атомов дали для большин- ства из них значение порядка нескольких магнетонов Бора.
Рассмотрим теперь влияние магнитного поля на движение электронов в атомах. Пусть орбита электрона ориентирована так, что вектор орбитального магнитного момента 
состав- ляет с направлением 
некоторый угол a (рис.1.12). В данном случае на орбиту электрона будет действовать вращательный момент
, (1.61)
под действием которого векторы 
и 
будут совершать прецессию, т. е. конусообразное движение вокруг вектора 
. Угловая скорость прецессии совпадает по направлению с вектором индукции и определяется выражением
. (1.62)
| Рис.1.12 |
Из данной формулы следует, что скорость прецессии не зависит ни от угла a, ни от радиуса орбиты, ни от скорости электрона и, следовательно, одинакова для всех электронов, входящих в состав атома.
Прецессия электронных орбит приводит к появлению дополнительного тока
. (1.63)
Этот ток создает индуцированный магнитный момент, направленный против внешнего поля
. (1.64)
Здесь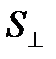 
- проекция площади орбиты на плоскость, перпенди- кулярную магнитному полю .
Наведение магнитного момента против поля свойственно всем атомам, находящимся в магнитном поле, и называется диамагнитным эффектом.
1.5.3. Диа -, пара - и ферромагнетики
К диамагнетикам относятся вещества, магнитные моменты атомов которых в отсутствие внешнего магнитного поля равны нулю. Диамагнетиками являются инертные газы, вода, стекло, мрамор, большинство органи- ческих соединений, многие металлы (висмут, цинк, золото, серебро, медь, ртуть и другие).
При внесении такого вещества в магнитное поле в каждом его атоме или молекуле за счет прецессионного движения электронных орбит наводится магнитный момент (1.64), направленный противоположно вектору , что приводит к уменьшению суммарного магнитного поля. Таким образом, для диамагнетиков магнитная восприимчивость имеет отрицательное значение, а магнитная проницаемость m < 1. Величина c диамагнетиков не зависит от температуры и напряженности магнитного поля. Процесс намагничивания диамагнетиков характеризуется линейной зависимостью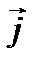 
от H (рис.1.13, кр.1).
К парамагнетикам относятся вещества, атомы которых в отсутствие внешнего магнитного поля обладают магнитным моментом.
Однако, намагниченность парамагнетика равна нулю, так как из - за теплового движения магнитные моменты атомов
ориентированы беспорядочно. При внесении парамагнетика в магнитное поле, наряду с возникшей прецессией электронных орбит и появлением индуцированного момента 
происхо- дит ориентация магнитных моментов атомов по направлению поля. При этом положительный магнитный момент оказывает- ся значительно больше, чем отрицательный индуцированный момент, в результате чего парамагнетик намагничивается по полю. Таким образом, процесс намагничивания парамагне- тиков во многом аналогичен тому, как поляризуется диэлект- рик, состоящий из полярных молекул.
Кривая намагничивания парамагнетика (рис 1.13, кр.2) свидетельствует о явлении насыщения, которое связано с ориентационным упорядочением магнитных моментов атомов вещества. Тепловое движение молекул препятствует этому процессу, поэтому в не очень сильных магнитных полях восприимчивость парамагнетика оказывается обратно пропор- циональной температуре
, (1.65)
где С – константа парамагнетика. Это соотношение носит название закона Кюри.
Парамагнетиками являются щелочные и щелочно- - земельные металлы, редкоземельные элементы, алюминий, платина, кислород, окись азота и другие вещества.
К ферромагнетикам относят вещества, которые обладают спонтанной (самопроизвольной) намагничено- стью. Типичные представители ферромагнетиков – это железо, кобальт, никель и их сплавы.
Характерной особенностью ферромагнетиков является нелинейная зависимость J (H) и B(H). Уже при небольших значениях H намагниченность достигает насыщения J нас (рис.1.14), тогда как зависимость B(H) продолжает расти с увеличением H по линейному закону (рис.1.15), согласно уравнению
B = m0H + m0Jнас.
| Рис.1.13 Рис.1.14 Рис. 1.15 |
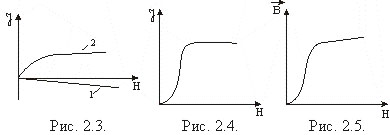
Ввиду нелинейной зависимости B(H) магнитная проницаемость ферромагнетика также является функцией H (рис.1.16). Вначале она быстро растет с увеличением H, достигает максимума, а затем убывает, стремясь к единице в очень сильных намагничивающих полях.
Второй отличительной особенностью ферромагнетиков является гистерезис намагничивания. При медленном циклировании магнитного поля получается петля гистере- зиса, внутри которой расположена основная кривая намагни- чивания (рис.1.17). Величина B ост называется остаточной индукцией, а Hк – коэрцитивной силой, представляющей собой напряженность размагничивающего поля, при котором остаточная индукция обращается в ноль. Площадь петли гистерезиса пропорциональна количеству теплоты, выделяю- щейся в единице объема ферромагнетика за цикл перемагни- чивания.
| Рис.1.16 |
| Рис.1.17 |
В зависимости от значения коэрцитивной силы различают магнитомягкие и магнитотвердые ферро- магнетики. Первые отличаются малым значением Hк и малыми потерями энергии при перемагничивании. Эти материалы используются для изготовления сердечников трансформаторов. Магнитотвердые материалы, характеризую- щиеся широкой петлей гистерезиса (Hк – велико), используются для изготовления постоянных магнитов.
Ответственными за магнитные свойства ферромагнетиков являются нескомпенсированные спиновые магнитные момен- ты электронов, взаимодействие которых приводит к возникно- вению областей спонтанного намагничивания, называемых доменами. Линейные размеры доменов порядка 
см. В пределах каждого домена ферромагнетик намагничен до насыщения и обладает определенным магнитным моментом. Направления этих моментов различны, так что в отсутствие внешнего поля суммарный момент ферромагнетика может быть равен нулю.
При постепенном увеличении напряженности внешнего магнитного поля 
происходит рост благоприятно ориенти- рованных доменов, т. е. тех доменов, моменты которых составляют с 
небольшой угол. На начальной стадии намагничивания этот процесс носит плавный и обратимый характер. В дальнейшем, из-за наличия в образцах различных дефектов, мешающих плавному смещению доменных границ, наблюдаются скачкообразные изменения J (эффект Баркгаузена). Наконец, в области близкой к насыщению, наблюдается поворот магнитных доменов в направлении поля. Последние процессы являются необратимыми, что и служит причиной гистерезиса.
Для каждого ферромагнетика имеется определенная температура Tс, при которой области спонтанного намагничи- вания распадаются, и вещество утрачивает ферромагнитные свойства. Эта температура называется точкой Кюри.
При температуре выше точки Кюри ферромагнетик становится обычным парамагнетиком, магнитная восприим- чивость которого подчиняется закону Кюри-Вейса
. (1.66)
При охлаждении ферромагнетика ниже точки Кюри его магнитные свойства восстанавливаются.
