Умова. Побудувати розгортку поверхні тіла завдання №8. Нанести на розгортку лінію перетину поверхні тіла і площини.
Один зі способів наближеного розгортання кривих поверхонь полягає в тому, що криву поверхню тіла замінюють вписаною в неї (або описаною) багатогранною поверхнею (див. завдання 8). Чим більше граней у вписаної поверхні, тим точніше результат. Для розгортки описаного багатогранника можна визначити натуральні величини його ребер і по них побудувати розгортку.
Приклад. Побудувати розгортку поверхні конуса, розглянутого в прикладі завдання 8 (рис. 17). Нанести на розгортку лінію перетину поверхні конуса і площини.
Рішення. Замінюємо конус вписаною в нього правильною пірамідою, що має 12 бічних граней (рис. І7,а). Бічні ребра цієї піраміди збігаються з твірними заданого конуса.
Ребра S1 l і S7, що є відрізками фронтальних прямих, відрізки 12S2 і 72S2, визначальні положення точок перетину на цих ребрах, проектуються на площину П1, у натуральну величину. Дія побудови розгортки проводимо дугу окружності радіусом, рівним довжині твірної конуса (рис. 17,б). Від точки 1 відкладаємо 12 разів хорду, рівну стороні основи вписаної піраміди (відрізок 1121 ). З'єднуючи точки 1-12 з центром окружності, одержуємо розгортку бічної поверхні вписаної піраміди. Кожен трикутник на розгортці (1S2, 2S3 і тд.) являє собою натуральну величину бічної грані піраміди. Основа піраміди збігається зі своєю горизонтальною проекцією. Горизонтальна проекція основи і розгортки бічної поверхні являють собою розгортку поверхні вписаної піраміди.
Бічна поверхня правильного прямого конуса може бути розгорнута в сектор окружності радіуса R рівного довжині утворюючого конуса, з кутом при вершині
α = (2r/R)360°
де r - радіус основи конуса. Однак для ілюстрації методу в розглянутому прикладі розгортку поверхні конуса замінимо розгорткою вписаної піраміди.
Для нанесення на розгортку лінії перетину потрібно показати на ній точки перетину, що лежать на ребрах S1-S12.
Положення точок перетину, що лежать на ребрах S1 і S7визначається відрізками Sl2 і S72. Дня нанесення на розгортку точок перетину, що лежать на інших ребрах, визначимо натуральну величину відстаней від цих точок до вершини конуса уздовж відповідних ребер, тобто натуральну величину відрізків S2, S3 і так далі, обертаючи їх навколо осі, що збігається з віссю конуса (навколо осі, перпендикулярної до площини П1 до положення, паралельного фронтальної площини проекцій). При цьому зазначені відрізки будуть проектуватися на площину П2 у натуральну величину.
Розглянемо, наприклад, відрізок S3. При обертанні його навколо осі конуса до положення, паралельного фронтальній площині проекцій, горизонтальна проекція точки 3 буде переміщатися по дузі окружності, радіуса S1 31 (рис 17,в) до положення, при якому цей радіус виявиться паралельним осі проекцій. Фронтальна проекція цієї точки буде, переміщатися по лінії, перпендикулярній до фронтальної проекції осі обертання (осі конуса) до зустрічі з фронтальною проекцією нарисової твірної S1 у точці 32 - Частина нарисової твірної від вершини S до точки 32 буде являти собою натуральну величину відстані від вершини конуса до точки перетину, що лежить на твірній S3. Відкладаючи на розгортці від центра S цю відстань уздовж твірної S3, знаходимо точку 3 (точку лінії перетину на цій
твірній). Інші точки ліній перетину на розгортці визначаємо аналогічно. З'єднуючи точки 1-12 плавною кривою, одержуємо на розгортці лінію перетину.
| Контрольні питання |
1) У чому полягає загальний метод одержання розгортки кривої поверхні?
2) Як наноситься на розгортку лінія перетину?
3) Чому отримана розгортка є наближеною?
4) Від чого залежить точність рішення задачі?
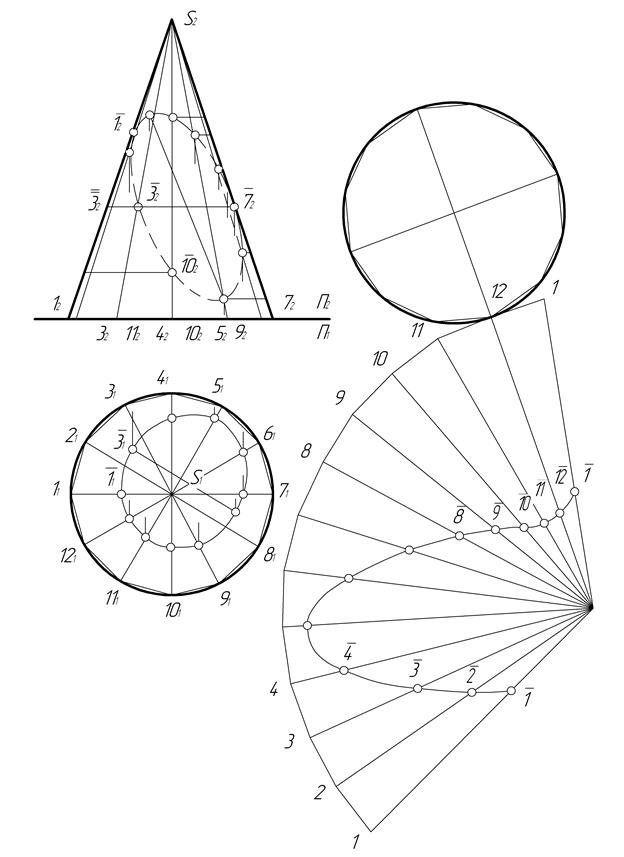
Рис. 17
| Завдання № 11 |






