Чернігівський національний педагогічний університет імені Т. Г. Шевченка
Кафедра ЗТД та креслення
НАРИСНА ГЕОМЕТРІЯ
НАВЧАЛЬНО-МЕТОДИЧНІ РЕКОМЕНДАЦІЇ
ДО ЛАБОРАТОРНИХ РОБІТ
Чернігів – 2016
У підготовці вчителя трудового навчання важливу роль відіграють предмет і методи нарисної геометрії.
Мета курсу - дати студенту знання, вміння і навички, що знадобляться майбутньому вчителю для викладу технічних думок за допомогою креслень, а також для розуміння по кресленню конструкції та принципу дії технічних виробів, що зображуються на кресленні. Варто підкреслити, що вивчення нарисної геометрії розвиває і тренує просторове уявлення студента, що необхідно не тільки в професійній діяльності вчителя трудового навчання, але й для успішного оволодіння такими дисциплінами, як математика, механіка, опір матеріалів, ТММ, деталі машин та ін.
Обов'язковою умовою засвоєння курсу нарисної геометрії є самостійне виконання студентом низки графічних завдань що охоплюють матеріал основних розділів курсу. Відповідно до цього студенти-заочники виконують дві контрольні роботи. Першу - під час установочної сесії. Другу у зазначений деканатом час на однім із консультпунктів першого семестру.
Контрольні роботи містять у собі по шість задач. Задачі 1-6 першої контрольної роботи студенти виконують у креслярському залі в присутності викладача, маючи можливість у процесі її підготування одержати необхідну консультацію. Шість задач другої контрольної роботи студенти виконують самостійно.
Варіанти завдань викладач видає на установчій сесії.
ВИМОГИ ДО ВИКОНАННЯ ГРАФІЧНИХ ЗАВДАНЬ
Графічні роботи повинні відповідати вимогам ЄСКД.
1.Індивідуальні завдання виконуються на креслярському папері формату А3 (297×420) ДЕРЖСТАНДАРТ 2.301-68. Рамку необхідно проводити, відступаючи 20 мм зліва і по 5 мм від інших сторін формату.
2.Побудова повинна виконуватися за параметрами, зазначеними у таблицях індивідуальних завдань, в масштабі 1:1 (у завданнях, де немає вказівок щодо розмірів, побудову варто виконувати так, щоб раціонально використати поле формату - 75% повинно бути заповнено рисунком і текстом.
3.Всі побудови потрібно виконувати олівцем типу ТІМ із дотриманням товщини ліній по ДЕРЖСТАНДАРТУ 2.303-68 (СТСЗВ 1178-78) за допомогою креслярських приладь чітко і охайно, тому що задача, виконана графічно неточно, вирішена невірно. Товщина ліній кожного типу повинна бути однакова для всіх зображень на даному кресленні.
Задані на епюрі проекції точок, а також точки, отримані в результаті побудови варто обводити циркулем колом діаметром 2-3 мм.
4.На форматі А3 у правому нижньому кусі, необхідно зазначити номер варіанта, групу, прізвище та ініціали студента (рисі).
5.Умова, завдання і правопис позначень повинні бути виконані креслярським шрифтом (тип Б з нахилом =75° відповідно до ДЕРЖСТАНДАРТУ 2.304-81.
6.Виконані графічні роботи згортаються до формату А4 (210×297) і зшиваються в альбом, що має титульний лист (рис. 2). Титульний лист повинен відповідати приведеному зразку. Він виконується тушшю шрифтом № 7, за винятком фрази "Практичні роботи", яка виконується прописними літерами шрифтом № 10.
| Завдання № 1 |
Умова. По заданим координатам точок (табл. 1) побудувати їх просторове комплексне креслення (епюр).
Координатою точки називають відстань від заданої точки до площини проекції. Наприклад, дані координати точки А: ОХ=60мм, ОY=20мм, OZ=65мм (див. рис. 1). Щоб побудувати просторове зображення, треба побудувати відповідний октант (тому що всі три координати точки А позитивні, сама точка розташована в першому октанті) і послідовно на осях X, Y,Z відкласти зазначені розміри.
Дані координати треба занести в таблицю, розміри якої рекомендовані 40×50 мм.
Далі по наочному зображенню треба побудувати епюр точок. Так, для побудови епюра точки А (60, 20, 65) потрібно відрізки, що відповідають координатам точки, відкласти на координатних вісях: по вісі X - 60 мм. Y- 20 мм, Z- 65 мм.
Після цього через отримані точки проводимо лінії зв'язку, у перетині яких відзначаємо шукані проекції точки: А1 - горизонтальна проекція. А2 - фронтальна і А3 -профільна.
| Контрольні питання |
1) Що називається епюром точки?
2) Що являє собою епюр Монжа?
3) Яка пряма на епюрі Монжа називається постійною прямою?
4) Як визначити положення координатних осей, якщо відомі три проекції точки?
| X | Y | Z | |
| A | |||
| B | |||
| C | |||
| D |

Рис. 1

Рис. 1 Закінчення

Рис.2
Таблиця 1
| № варіанта | А | В | С | D | |||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | ||
Продовження таблиці 1
| № варіанта | А | В | С | D | ||||||||||
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | |||
| 30_ | ||||||||||||||
| 33_ | ||||||||||||||
| 5С | ||||||||||||||
| 49_ | ||||||||||||||
| _ 83_І | ||||||||||||||
| Завдання №2 |
ПРЯМА
Умова. Встановити положення ребер багатогранника щодо площин проекцій. Визначити натуральний розмір одного з ребер загального положення та його кути з площинами проекцій. Знайти горизонтальний слід М(М1M2) і фронтальний слід N(N1N2) одного з ребер загального положення. Точкою К(К1,К2) розділити одне з ребер загального положення у відношенні 2:3 (схема мал. 3).
Дослідження положення ребер щодо площин проекцій починається з позначення вершин багатогранника (мал. 4). У процесі позначення кожне ребро думкою виділяється і по уявленню записується його положення: горизонтальне, фронтальне, профільне і т.д.
Щоб визначити натуральний розмір і кути нахилу до площин проекцій ребра загального положення, необхідно зробити додаткові побудови, наприклад, способом прямокутного трикутника. Натуральний розмір відрізка прямої загального положення дорівнює гіпотенузі прямокутного трикутника, одним катетом якого є одна з проекцій даного відрізка, а іншим - різниця відстаней від кінців іншої проекції відрізка до вісі проекцій. Отримані кути α і β. визначають відповідно куги нахилу даного ребра до площин проекцій П1 і П2.
Для того щоб знайти горизонтальний слід, необхідно продовжити фронтальну проекцію А2S2 до перетинання з віссю X, потім через точку перетинання (фронтальну проекцію горизонтального сліду) провести перпендикулярну пряму до вісі X до перетинання з продовженням горизонтальної проекції А1S1. Точка перетинання М1 є горизонтальною проекцією горизонтального сліду, вона співпадає з самим слідом (= - знак слівпадання).
Для знаходження фронтального сліду необхідно продовжити горизонтальну проекцію А1S1 до перетинання з віссю проекцій, через точку N1. (горизонтальну проекцію фронтального сліду) провести перпендикуляр до перетинання з продовженням фронтальної проекції А2S2. Точка N2 є фронтальною проекцією фронтального сліду, вона збігається із самим слідом.
На рис.4 відрізок АS розділений у відношенні 2:3. З точки А1 проведена під довільним кутом допоміжна пряма, на якій відкладені п'ять (2+3) відрізків довільної довжини, але рівних між собою: А1К0=2, К0S0=3. З'єднуючи точку S0 із проекцією S0 і проводячи з точки К0 пряму, рівнобіжну S0S1 одержуємо точку К1 (причому А1,К1: К1 - 2:3) і потім знаходимо К2 Точка К поділяє відрізок АS у відношенні 2:3.
| Контрольні питання |
1) Як зображуються на епюрі прямі загального і часного положення?
2) Які прямі зображуються на проекціях у натуральну величину?
3) Що являє собою слід прямої лінії?
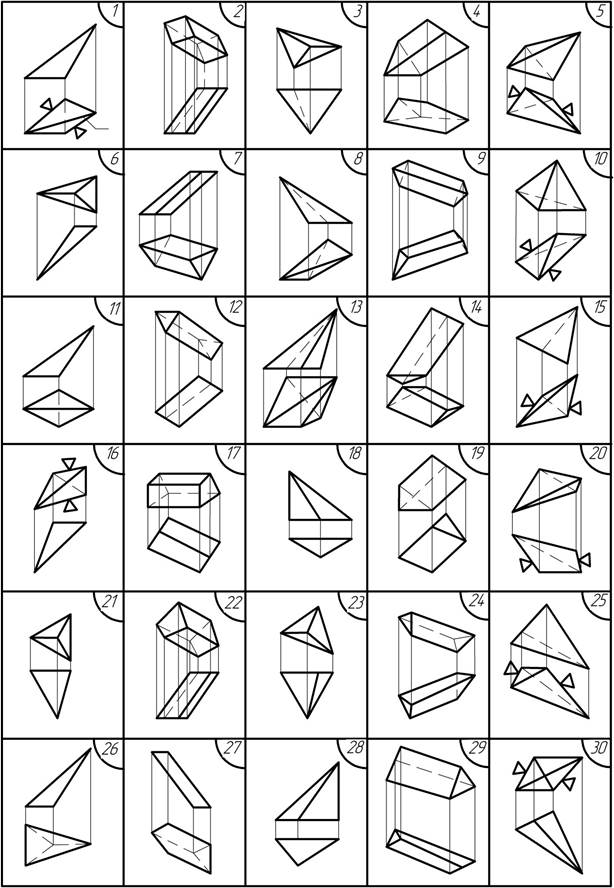
Рис. 3

Рис. 3 Продовження

Рис. 3 Закінчення

Рис. 4
| Завдання № 3 |
Визначити точку перетину прямої з площиною загального положення. Встановити видимість прямої на проекціях (рис. 5. табл. 2).
Таблиця 2
| Кут № | |||
| α0 | |||
| β0 |
Рішення задач на побудову точки перетину прямої і площині може бути розбите на три етапи.
1. Пряму l заключають у допоміжну площину Q (рис. 6).
2. Визначають лінію перетинати заданої площини Р з допоміжною площиною Q (лінія ЕF)
3. Знаходять точку перетину заданої прямої і площини як точку перетину прямої і лінії перетину заданої і допоміжної площин (точка К).
Приклад. Визначити точку перетину прямої l Із площиною трикутника АВС. Встановити "видимість" (рис. 7).
1. Укладаємо пряму l у допоміжну площину. В якості допоміжної приймаємо фронтально-проектуючу площину Т, h - горизонтальний слід цієї площини, а f - фронтальний. Оскільки площина Т фронтально-проектуюча, фронтальна проекція лежачої в ній прямої збігається з фронтальним слідом цієї площини.
2. Визначаємо лінію перетину площини трикутника АВС і допоміжної площини T. Для знаходження лінії перетину двох площин досить визначити дві точки, загальні для цих площин (тому що площини перетинаються по прямій, а дві точки визначають пряму). Загальними для двох зазначених площин с точки перетину сторін АВ і АС трикутника АВС з допоміжною площиною Т.
Точка M2 є фронтальною проекцією точки перетину сторони АС трикутника з допоміжною площиною Т, а точка N2 - сторони А. Проводячи з цих точок лінії зв'язку до перетину з горизонтальними проекціями відповідних сторін трикутниками АВС, одержуємо горизонтальні проекції цих точок (М1 і N1). Відрізок М1N1, визначає горизонтальну проекцію лінії перетину заданої і допоміжної площин.
3. Горизонтальною проекцією шуканої точки перетину заданої прямої і площини є точка К1 -
точка перетину з горизонтальною проекцією лінії перетину заданої і допоміжної площин М1N1 з
горизонтальною проекцією заданої прямої.
По лінії зв'язку визначаємо фронтальну проекцію цієї точки К2. Для встановлення "видимості" використовуємо спосіб конкуруючих точок.
У точці N2=I2 збігаються фронтальні проекції точок 1 і N, перша з яких належить прямій l, а друга - стороні АВ трикутника. Йдучи по лінії зв'язку вниз від цієї точки, спочатку зустрічаємо горизонтальну проекцію точки прямої (точка К,). а потім - сторони АВ трикутника (точка N1). Отже, точка I (точка прямої) розташована ближче до площини проекцій П> ніж точка М, і на фронтальній проекції в цьому місці сторона трикутника перекриває пряму.
Аналогічно, йдучи по лінії зв'язку вгору від точки 21–31 спочатку зустрічаємо фронтальну проекцію точки 2, що належить до прямої I, а потім - точки 3. що належить стороні ВС трикутника. Отже, точка 3 сторони ВС трикутника лежить вище точки 2 прямої і на горизонтальній проекції сторона трикутника в цьому місці перекриває пряму
Приклад. Визначити точку перетину прямої l із площиною загального положення, заданої слідами (рис. 8). Зазначити "видимість" прямої на проекціях.
План розв'язку цієї задачі такий же, як і розглянутої в прикладі 1.
Спочатку проведемо через задану пряму допоміжну площину фронтально-проектуючу T (її сліди h0f0). Потім будуємо лінію перетину заданої і допоміжної площин. Ця лінія визначається двома точками, загальними для обох площин. Одна з цих точок (М) лежить на перетині горизонтальних слідів заданої і допоміжної площин. Вона знаходиться в площині П1, і збігається зі своєю горизонтальною проекцією М1. Фронтальна ж проекція цієї точки є точка М2.
Друга загальна для двох площин точка лежить на перетині фронтальних слідів площин
Q і Т, Це точка N, що лежить у фронтальній площині проекцій і тому співпадає зі своєю фронтальною проекцією. Горизонтальна проекція цієї точки - точка N2,. З'єднуючи точки М1 і
N1, одержуємо горизонтальну проекцію лінії перетину заданої і допоміжної площин (пряма М1N1).
Точка перетину цієї проекції з горизонтальною проекцією заданої прямої і є горизонтальною проекцією шуканої точки перетину прямої і площини (точка К1). По лінії зв'язку визначаємо фронтальну проекцію цієї точки (точка К2).
"Видимість" на кресленні можна встановити виходячи з наступних розумінь.
Точка 1 горизонтального сліду площини Qзбігається з горизонтальною проекцією точки 2 прямої 1. На фронтальній проекції видно, що в цьому місці пряма розташована над горизонтальною площиною проекцій П1, і, відповідно, частина прямої аж до точки її перетину з площиною Q при погляді зверху буде видима. Аналогічно можна встановити "видимість" на фронтальній проекції.
| Контрольні питання |
1) Яким способом може бути задана площина на епюрі?
2) Дайте визначення прямих загального і часного положення.
3) Дайте визначення площин загального і часного положення.
4) План рішення задачі на перетин прямої і площини.
5) У чому полягає спосіб конкуруючих точок для встановлення "видимості" елементів на кресленні?

Рис. 5

Рис. 5 Закінчення

Рис. 6

Рис. 7

Рис. 8
| Завдання №4 |






