На заданому багатограннику визначити натуральний розмір двогранного кута при ребрі АS (див. рис. 3).
У завданнях на поличці-зносці зазначене ребро двогранного кута, розмір якого обхідно визначити.
Мірою двогранного куга є кут, сторони якого розташовані відповідно у гранях двогранного кута і перпендикулярні до його ребра. Для визначення розміру двогранного кута його необхідно спроектувати на площину, перпендикулярну до його ребра При цьому лінійний кут при даному ребрі виявиться рівнобіжним площині проекцій і спроектується на неї в натуральну величину.
Площину, перпендикулярну до ребра, можна побудувати так само, як, наприклад, у завданні №3 - методом заміни площин проекцій, при якому положення самого тіла змінюється. Але можна, навпаки, залишити нерухомими площини проекцій, а переміщати тіло до потрібного положення. У даному випадку можна перемістити двогранний кут у положення, при котрому його ребро виявиться перпендикулярним до однієї з площин проект шляхом двох послідовних плоскопаралельних переміщень.
Нагадаємо, що при плоскопаралельному переміщенні тіла його точки переміщуються в площинах, рівнобіжних деякій площині, наприклад П1 проекція тіла на цю площину змінює свою величину і форму, а змінює тільки положення, проекції точок тіла на перпендикулярну площину (П2) переміщуються по прямолінійних траєкторіях, рівнобіжних вісі проекцій.
Відповідно до цього в прикладі на рис. 10 спочатку переміщуємо піраміду плоскопаралельно відносно П1 до положення, при якому ребро SА виявиться рівнобіжним П2 (стане фронтальною прямою).
При цьому його горизонтальна проекція S1А1, зберігши свій розмір, розташується паралельно вісі проекцій. Добудовуємо на ній горизонтальну проекцію піраміди в новому положенні - без зміни розмірів і форми.
Проводячи лінії зв'язку з отриманих вершин до перетину з горизонтальними траєкторіями переміщень фронтальної проекції вершин піраміди, одержуємо фронталь: проекцію піраміди в новому положенні.
Друге плоскопаралельне переміщення робимо щодо площини П2 - до положення, якому ребро SА виявиться перпендикулярним доплощини П1). При цьому його фронтальі проекція повинна бути перпендикулярна вісі проекцій, а горизонтальна, зрозуміло, являє собою точку. Тому вертикально
креслимо відрізок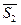 
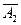.2 рівний по розмірі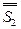 
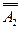і на ньому без зміни величини і формидобудовуємо фронтальну проекцію піраміди в положенні після першого переміщення.
Горизонтальну проекцію після другого переміщення будуємо тільки для двогранного кута, що нас цікавить. Він утворюється, як і в першому випадку, за допомогою ліній зв'язку траєкторій переміщення горизонтальних вершин піраміди з положення, у якому він виявив після першого переміщення.
Як видно з побудови на рис. 10, горизонтальна проекція двогранного кута перетворилась в кут α, рівний лінійному куту, що визначає даний двогранний кут.
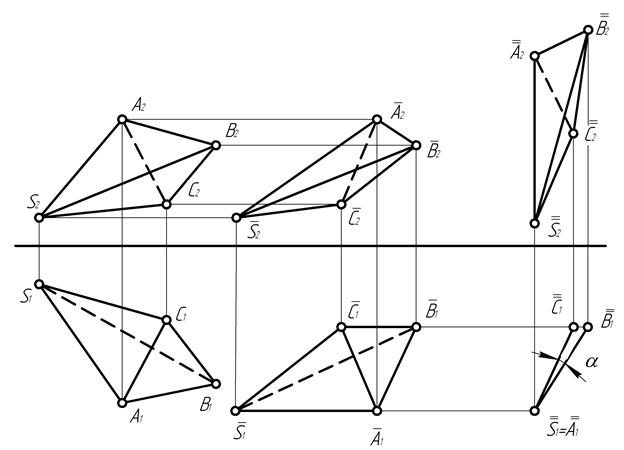
Рис. 10
| Завдання № 6 |
