Умова. По двох даних проекціях побудувати третю й аксонометричні проекції сполучення фігур - косокутну фронтальну диметрію і прямокутну ізометрію (рис. 25, табл.8).
Таблиця 8
| Діаметр | ||||||
| d, мм | ||||||
| h, мм |
Примітка: d - діаметр циліндра; h - висота піраміди або призми.
При побудові косокутної фронтальної диметрії просторовий координатний трьохгранник, твердо зв'язаний з предметом, що зображується, розміщується так, що його осі Х1 і Z1 паралельні площині аксонометричних проекцій, а вісь Y1 перпендикулярна до неї.
При цьому усі відрізки і фігури, розташовані в площинах, паралельних площині Х1O1Z1 просторового тригранника, проектуються на площину аксонометричних проекцій у натуральну величину, тобто коефіцієнти викривлення по осях Х1 і Z1 рівні 1. Напрямок проектуючих променів щодо осі їївибирається так, що проекція цієї осі (аксонометрична вісь Y) розташовується під кутом 135° до аксонометричних осей Х і Z що являють собою проекції осей Х1 і Z1 просторового тригранника (коефіцієнт викривлення по осі К дорівнює 0,5, рис. 26). Це значить, що усі відрізки, паралельні осі Y1 зображуються на аксонометричній площині проекцій у половину своєї натуральної величини.
Побудова зображень окружностей у косокутній фронтальнійдиметрії
Окружності, розташовані в площинах, рівнобіжних площині Х1O1Z1, (і площиниаксонометричних проекцій, проектуються в натуральну величину.Наближенозображення окружностей, розташованих у площинах, рівнобіжних площинам Х1O1Z1 і Y1O1Z1, можна побудувати по точках, як показано на рис. 27.
Приклад 1. Побудувати косокутну фронтальну диметричну проекцію циліндра і піраміди (рис. 26)
Піраміду розташовуємо в просторі так, щоб її висота співпала з віссю Z1 центр рівностороннього трикутника основи піраміди з початком координат, а вершина основи З1 знаходилася на осі Х1.
Тоді на аксонометричному кресленні висоти піраміди (О1S1 і основи 31К1 як відрізки, рівнобіжні осям X1і Z1) зобразяться в натуральну величину. При цьому центр координат поділяє висоту основи у відношенні 1:2. Сторона основи 1121 паралельна осі Y1 зобразиться на аксонометричному кресленні в 1/2 натуральної величини (зображення буде паралельно осі Y1 відрізок 12). З'єднавши точки 1, 2. З між собою і з точкою S, одержимо аксонометричне зображення піраміди.
Вісь циліндра в просторі розташована в площині Х1O1Z1 паралельно осі O1Х1 на відстані радіуса циліндра від цієї осі. Тому відстань між центрами основ циліндра по осі зобразиться внатуральну величину (відрізок 
 , рівнобіжний осі X знаходиться від неї на відстані радіуса циліндра). Потім на кресленні проводимо системи аксонометричних осей з центрами в точкахпроекцій кінців осі циліндра
, рівнобіжний осі X знаходиться від неї на відстані радіуса циліндра). Потім на кресленні проводимо системи аксонометричних осей з центрами в точкахпроекцій кінців осі циліндра  і
і  будуємо зображення окружностей основ циліндра в відповідності з рис. 27 (на рис. 26 ця побудова не показана).
будуємо зображення окружностей основ циліндра в відповідності з рис. 27 (на рис. 26 ця побудова не показана).
При побудові зображення в прямокутній ізометрії просторовий координатний тригранник розташовується перед площиною аксонометричних проекцій так, що осі координат Х1Y1Z1, нахилені до площини проекцій під однаковими кутами, а промені, що
проектують, спрямовані перпендикулярно до цієї площини. При цьому аксонометричні осі Х,Y,Z, розташовуються під кутом 120° одна до одної (рис. 28). Коефіцієнт викривлення по всіх осях однаковий і дорівнює 0,82. У технічному кресленні коефіцієнт викривлення для простоти умовно приймається рівним 1, тобто відрізки прямих на зображуваному предметі, рівнобіжні осям координатного тригранника, зображуються на аксонометричній площині проекцій у натуральну величину. При цьому аксонометричне зображення виявляється збільшеним у 1:0,82 = 1,22 рази.
Побудова зображень окружності в прямокутній ізометрії
Цю побудову наближено можна робити так, як показано на рис. 28. Якщо окружність знаходиться в площині Х1Y1Z1 будується ромб 0234 зі сторонами, паралельними аксонометричним осям X і Y, і рівними натуральній величині діаметра проектуємо окружності (діаметри окружності, рівнобіжні осям X, і Y. проектуються в натуральну величину). Потім з точки О радіусом ОA проводимо дугу АВ окружності. Аналогічно з точки 3 тим же радіусом проводимо дугу ВD. Далі з точки К радіусом КА проводимо дугу АD і з точки Н тим же радіусом - дугу ЕС.
Аксонометричні проекції окружностей, що лежать у площинах, рівнобіжних площинам Х1O1Y1 і Y1O1Z1 будуються аналогічно (рис, 28).
Приклад 2. Побудова прямокутної ізометричної проекції (рис. 29).
Розглядаються ті ж геометричні тіла, що при побудові косокутної диметріі в попередньому прикладі.
Центр основи піраміди сполучаємо з початком просторової системи координат, а висоту піраміди - з віссю Z1. Відкладаючи на аксонометричній осі Zвідпочатку координат натуральну величину висоти піраміди, одержуємо точку S - аксонометричну проекцію вершини піраміда (умовно приймаємо, що відрізки, рівнобіжні просторовим осям координат, проектуються в натуральну величину).
Піраміду розташовуємо так, що одна з висот основи, що збігається з віссю X1 проектується (відповідно до нашої умови) у натуральну величину (відрізок КЗ). причому початок координат поділяє її у відношенні 1:2. Через точку К проводимо паралельно осі Y відрізок 12, дорівнює натуральній величині сторони основи піраміди, тому що ця сторона основи паралельна просторовій осі Y1. З'єднуючи між собою точки 1,2. 3 прямими, одержуємо аксонометричну проекцію основи піраміди, а з'єднуючи їх із точкою S - проекцію піраміди.
Відрізок 
 , що представляє собою проекцію відрізка між центрами основ по осі циліндра, розташується паралельно осі X відстані радіуса циліндра. У просторі цей відрізок рівнобіжний осі Х1 і тому на аксонометричній проекції відкладається в натуральнувеличину.
, що представляє собою проекцію відрізка між центрами основ по осі циліндра, розташується паралельно осі X відстані радіуса циліндра. У просторі цей відрізок рівнобіжний осі Х1 і тому на аксонометричній проекції відкладається в натуральнувеличину.
Проводимо системи аксонометричних осей з центрами в точках 
 будуємо аксонометричні зображення основ циліндра, що розташовані в площинах, рівнобіжних координатній площині Y1O1Z1 у відповідності до рис. 28. Потім проводимо відрізки 45 і 67, дотичні до зображень основ циліндра і рівнобіжні осі
будуємо аксонометричні зображення основ циліндра, що розташовані в площинах, рівнобіжних координатній площині Y1O1Z1 у відповідності до рис. 28. Потім проводимо відрізки 45 і 67, дотичні до зображень основ циліндра і рівнобіжні осі 
 , Ці відрізки утворять аксонометричне зображення циліндра.
, Ці відрізки утворять аксонометричне зображення циліндра.
| Контрольні питання |
1) Як будується зображення у фронтальній косокутній диметрії?
2) Як будується зображення в прямокутній ізометрії?
3) Як будується зображення окружностей у зазначених видах аксонометрій?

Рис. 25

Рис. 25 Продовження

Рис. 25 Закінчення

Рис. 26

Рис. 27
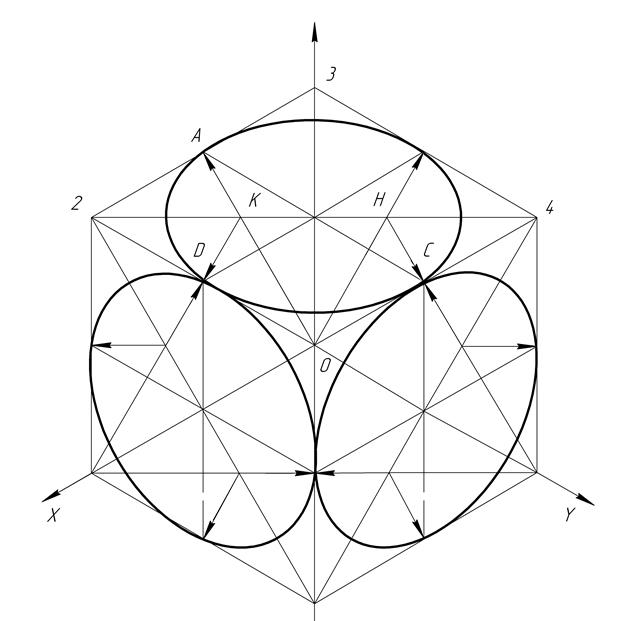
Рис. 28

Рис. 29
ЛІТЕРАТУРА
1. Гордон В.О.. Семенцов-Огиевский МА. Курс начертательнойгеометрии. - М.: Наука. 1977.
2. Посвянский Л.Д. Краткий курс начертательнойгеометрии. - М: Высш. шк.. 1974
3. Локтев О.В. Краткий курс начертательнойгеометрии. - М.: Вьісш. шк., І985.
4. Гордон В.О. Дванов Ю.Б., Солнцева ТЕ. Зборник задач по курсу начертательнойгеометрии. - М: Наука. 1977.
ЗМІСТ
Частина перша Частина 3
Вимоги до виконань графічних завдань 3
Завдання 1. Точка 4
Завдання 2. Пряма 10
Завдання 3. Перетин прямої та площини загального положення 15
Завдання 4. Спосіб зміни площин проекцій 21
Завдання 5 Плоско-паралельне переміщення 24
Завдання 6. Дві взаємно перпендикулярні площини 26
Завдання 7. Метод обертання навколо ліній рівня (горизонталі або фронталі) 30
Література 34
Частина друга 35
Завдання 8. Перетин багатогранної поверхні площиною 36
Завдання 9. Перетин кривої поверхні площиною загального положення 40
Завдання 10. Побудова розгортки поверхні тіла 45
Завдання 11. Перетин геометричних тіл прямою лінією 48
Завдання 12. Побудова лінії перетину поверхонь геометричних тіл 53
Завдання ІЗ. Побудова аксонометричних проекцій тіла 59
Література 68






