Следующие законы являются следствием соответствующих законов логики высказываний. Перечислим эти законы.
1. Коммутативность пересечения: 
.
2. Коммутативность объединения: 
.
3. Ассоциативность пересечения: 
.
4. Ассоциативность объединения: 
.
5. Дистрибутивность пересечения относительно объединения: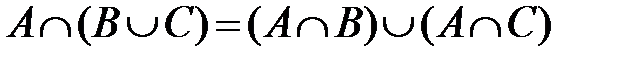 
.
6. Дистрибутивность объединения относительно пересечения: 
.
7. Закон де Моргана относительно пересечения: 
.
8. Закон де Моргана относительно объединения: 
.
9. Закон поглощения для объединения: 
.
10. Закон поглощения для пересечения: 
.
11. Закон идемпотентности для пересечения: 
.
12. Закон идемпотентности для объединения: 
.
13. Закон противоречия: 
.
14. Закон исключения третьего: 
.
15. Закон двойного отрицания: 
.
16. 
, 
.
17. 
, 
.
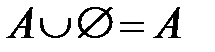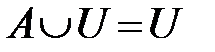Для доказательства равенств, присутствующих в законах, следует показать, что множества, стоящие по обе стороны знака равенства, состоят из одних и тех же элементов.
Приведем пример доказательства закона 6.
а) Пусть 
. Все использованные нами импликации основываются на определениях. Теперь применим к последнему высказыванию шестой закон логики высказываний. Получим 
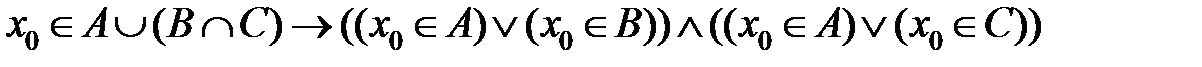. В соответствии с определениями пересечения и объединения множеств имеем 
. Таким образом,
.
б) Пусть 
, что следует из определений пересечения и объединения. Теперь согласно шестому закону логики высказываний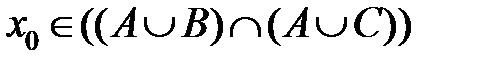 
, и снова из определений объединения множеств и пересечения множеств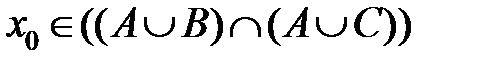 
.
Доказательство закончено.
Студенты должны самостоятельно доказать все равенства, приведенные в законах теории множеств, основываясь на соответствующих равенствах в законах логики высказываний, и убедиться в том, что такие разные разделы математики, как математическая логика и теория множеств, могут иметь сходные свойства с точки зрения действующих там законов.
Используя законы теории множеств, легко упрощать представление множеств, заданных с помощью последовательности операций.
Пример. 
Задания
1. Прочтите записи и перечислите элементы каждого из множеств:
A = {x| x ∈N, x < 5}; D = {x| x ∈Z, −5< x ≤ 2}; E = {x |x ∈Z, −3 ≤ x ≤ 2}.
2. Установите, какое из подмножеств А или В является подмножеством другого множества, если: 1) А={1; 2; 3;... 10}, В={2; 4; 6;8}; 2) А={2; 4; 6; 8; 10}, В - множество чисел первого десятка; 3) А – множество четных однозначных чисел, В - множество однозначных чисел, кратных 4; 4) А- множество двузначных натуральных чисел, В - множество четных двузначных чисел; 5)А=N, D=No; 6) A=N, B=Z; 7) A=R, B=Z.
3. Заданы множества: А={3,5,7,а,с}; В={а,р,с,3,5,6,7}; С={а,3,с,7}. Расположите их так, чтобы каждое из них было подмножеством следующего за ним.
4. Пусть А – множество всех натуральных делителей числа 18; В – множество всех натуральных делителей числа 24. Найти: 1) множество общих делителей чисел 18 и 24; 2) самый большой общий делитель.
5. Найдите пересечение и объединение множества А различных букв, входящих в слово “педагогика”, и множества В различных букв, входящих в слово “математика”.
6. Пусть даны множества А, В, С. Найдите А∩В, А∩С, В∩С, А∪В, А∪C, В∪С, если:
1) А={2; 3; 8; 9}, В={16; 18; 20}, C=N; 2) A=N, B={-2; -1; 0; 1; 2}, C={3; 5; 7};
3) A={3; 4; 5;...}, B=N, C={-1; 0; 1; 2}; 4) A={21; 22;...; 26}, B={3; 5}, C=N.
7. Заданы множества А={1,2,3,5,а,с}, В={1,2,3,р,а}, С={5,с}. Какие из приведенных соотношений: 1) В 
А,2) С А, 3) А\В=С, 4) А∩В=С, 5) А∩С=С верны?
8. Найти пересечение и объединение множеств:1) [3; 4] и [2; 6]; 2) (-1; 3) и (-4; 2]; 3) (-2; 1] и [-2; 0); 4) (-∞; 3) и (-1; ∞); 5) A=[-2; 3], B=(1; 5]; 6) A=[-1; 4], B=[1; 2); 7) A=(-∞; 2), B=[-3; ∞). (Указание. Для решения использовать числовую прямую).
9. Дано: A={1; 2; 3}, B={2; 4}, C=[2; 8]. Найдите результат следующих операций:
1) А∩(В∪С); 2)А∪(В∩С); 3)(А∪В)∩С; 4)(А∩С)∪(А∩В).
10. Найдите результаты операций для каждой тройки множеств А, В, С:
1) А∪(В∩С); 2) (А∩В)∩С; 3) А∩(В∪С); 4) (А∩В)∪С, если
а) А=(0;2], В=[-1; 3], С=(-3; 6); б) А=(-3; 6), В=[0; 4), С=[2; 7].
11. Найти разности А\В и В\А множеств А и В, если: 1) А={1; 2; 3;...; 10}, B={5; 6;...; 12}; 2) А – множество натуральных делителей числа 18; В – множество натуральных делителей числа 24; 3) А – множество правильных многоугольников, В – множество прямоугольников; 4) A={x|x∈R, 2≤x≤6}, B={ x|x∈R, 3≤x≤7}; 5) A={x|x∈R, 1<x≤4}, B={x|x∈R, 2<x≤8}; 6) A={x|x∈R, 0<x<2}, B={ x|x∈R, 1<x≤3}.
12. Для множеств А, В, С общего положения (т.е. А∩В∩С≠∅) на диаграмме Эйлера изобразить множества
1) (А∪С)\В; 2) (А\С)∪В; 3) (А∩В)\С; 4) (А∪В)∩С.
Элементы теории графов.
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.
Понятие графа
Рассмотрим две задачи.
Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до Марса нельзя.
Задача 2. Доска имеет форму двойного креста, который получается, если из квадрата 4x4 убрать угловые клетки.
Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу?
Решение: Занумеруем последовательно клетки доски:
А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:
Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями.
Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например. если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.
Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:
Такие одинаковые, но по-разному нарисованные графы, называются изоморфными.
