Пусть функция 
задана на множестве 
и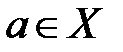 
. Если 
, то говорят, что эта функция непрерывна в точке 
. Функция, непрерывная в каждой точке множества 
, называется непрерывной на множестве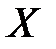 
. График непрерывной функции представляет собой непрерывную кривую. Все известные из школьного математического курса функции непрерывны в областях, где они заданы: многочлены, 
, 
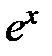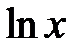при 
, 
, 
, 
при 
, 
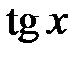при 
.
Пример разрывной функции – функция 
Графиком непрерывной на области D функции двух переменных 
является непрерывная поверхность. В качестве примера приведем функцию 
.
Частным случаем непрерывной в точке функции является дифференцируемая в этой точке функция. Такие функции еще называют «гладкими»: к графику дифференцируемой в точке функции можно провести касательную.
В случае дифференцируемости функции в точке можно вычислить производную в такой точке по формуле
.
Очевидно, что существуют непрерывные кривые, в некоторых точках которых провести касательную невозможно.
Напомним, что геометрическим смыслом производной 
является тангенс угла наклона касательной к кривой 
в точке 
.
Из школьного курса вам известна таблица производных. Она приводится ниже.
Таблица производных
 , если  постоянная
| 
| 
| 
|
| 
| 
| 
|
| 
| 
| 
|
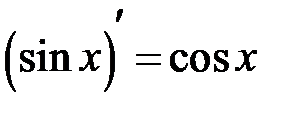
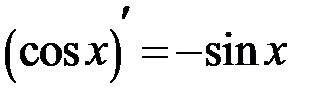
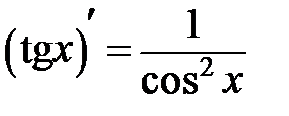
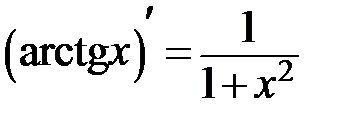
| X |
| Y |
| 0 |
|
|
|
Определение 1. Функция 
в точке 
имеет максимум, если для всех x из некоторой 
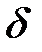-окрестности точки выполняется неравенство 
при 
.
| X |
| Y |
| 0 |
|
|
|
в точке 
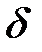имеет минимум, если для всех x из некоторой -окрестности точки 
выполняется неравенство 
при 
.
Определение 3. Точки максимума и минимума функции называются точками экстремума.
Теорема о необходимом условии экстремума дифференцируемой функции одной переменной: необходимым условием экстремума дифференцируемой в точке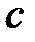 
функции является 
.
Точки, в которых производная функции обращается в ноль, называются критическими точками. Критические точки функции не обязательно являются точками экстремума. Например, если 
, то 
при 
, но точка 
не является точкой экстремума, что видно из рисунка.
Теорема о достаточном условии существования максимума и минимума функции.
| + max - |
| - min + |
меняет знак с + на –, это точка максимума. Если знак производной меняется с – на +, имеем точку минимума. Доказательство следует из теоремы о возрастании (убывании) функции.
В случае, когда дифференцируемой в точке является функция двух переменных , она обладает в этой точке производными и по переменной x, и по переменной y. Такие производные называются частными производными. График такой функции в этой точке (поверхность) является гладким, то есть к поверхности в точке можно провести касательную плоскость.
Теорема о необходимом условии экстремума дифференцируемой функции двух переменных: необходимым условием экстремума дифференцируемой в точке (a,b) функции является равенство нулю обеих частных производных этой функции: 
. 
.
Последнее условие является основой для следующего важного метода.
