Пример. Пусть опыт состоит в однократном бросании игральной кости, а событие 
– выпадение нечетного числа. Всего исходов 6 (1, 2, 3, 4, 5, 6), из них 3 благоприятствуют событию (1,3,5). Таким образом, 
.
Пример. Вернемся к нашему опыту бросания двух монет. Вычислим вероятности событий, составляющих множество исходов: 
– «выпало два герба», 
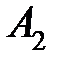– «выпали две цифры», 
– «выпал один герб и одна цифра». Если каждое из первых двух событий соответствует одному исходу: одновременное выпадение либо гербов, либо цифр у монет, условно названных первой и второй, то событию благоприятствуют следующие исходы: «герб на первой монете и цифра на второй» и «цифра на первой монете и герб на второй». Таким образом, если сосчитать равновероятные исходы с учетом номера монет, то их 4: ЦЦ, ГГ, ГЦ, ЦГ. Следовательно, 
, 
.
Большую роль в решении задач об опытах с равновероятными исходами играют комбинаторные функции.
Пример. В ящике лежат 20 одинаковых на ощупь шаров, из них 12 белых и 8 черных. Наудачу вынимают 2 шара. Какова вероятность того, что оба они белые?
Определим число возможных исходов выбора двух шаров из 20. Это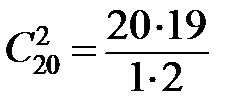 
. Благоприятных исходов 
. Таким образом, вероятность выбора двух белых шаров равна 
.
Часто для вычисления вероятностей пользуются теоремой сложения, согласно которой 
. В частности, если события 
и 
несовместны, 
. Следствием теоремы сложения является формула 
.
Пример. Стрелок попадает в десятку с вероятностью 0,05, в девятку – с вероятностью 0,2, в восьмерку – с вероятностью 0,6. Какова вероятность при одном выстреле выбить не менее восьми очков?
Интересующее нас событие является объединением попарно не пересекающихся событий: «выбито 8 очков», «выбито 9 очков» и «выбито 10 очков». Следовательно, в соответствии с теоремой сложения для вычисления требуемой вероятности следует сложить вероятности всех этих событий и получить 0,85.
Пример. В ящике лежат 8 белых и 12 красных одинаковых на ощупь шаров. Какова вероятность, вынимая наугад 3 шара, вынуть хотя бы один белый?
В данном случае можно сосчитать вероятности вынуть 3 белых, 2 белых и один красный и 1 белый и 2 красных шара, а затем сложить полученные величины. Однако рациональнее сосчитать вероятность противоположного события – вероятность вынуть три красных шара. Итак, 
. Следовательно, 
.
Пусть два события 
и 
независимы, то есть, от того, произойдет или нет одно из них, не зависит наступление второго. Для независимых событий определяют вероятность пересечения событий как 
.
Пример. Два самолета сбрасывают по бомбе на вражеский объект. Объект считается уничтоженным, если в него попали две бомбы. Какова вероятность уничтожить объект, если вероятность попадания первого самолета 0,8, а второго – 0,75?
Очевидно, что если летчик не отслеживает попадание в цель товарища и не укрепляет (или ослабляет) тем самым свой моральный дух, попадание бомб из разных самолетов в цель – взаимно независимые события. Поэтому вероятность одновременного попадания в цель равна 
.
Пример. В условиях предыдущего примера следует подсчитать вероятность попадания в цель хотя бы одного летчика.
Благоприятными для наступления интересующего нас события являются следующие исходы: «попали оба», «первый попал, второй не попал», «первый не попал, второй попал». Вероятность первого из исходов 0,6, вероятность второго 
, вероятность третьего 
. Поэтому вероятность попадания хотя бы одного летчика равна 
. В соответствии со следствием из теоремы сложения тот же результат мы получим, подсчитав вероятность противоположного события «в цель не попали оба летчика» (
) и вычтя полученный результат из единицы.
В ряде случаев возникает вопрос: что можно сказать о вероятности события 
, если известно, что произошло событие 
? Вероятность при этом обозначается 
и читается «вероятность при условии ». Если события и несовместны, то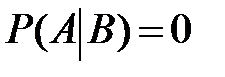 
, то есть – невозможное событие при наступлении события . Если, наоборот, 
, то 
, то есть, при событие при условии – достоверное событие. Для случаев, когда при условии событие может как наступить, так и не наступить, вводят понятие условной вероятности, вычисляемой по формуле: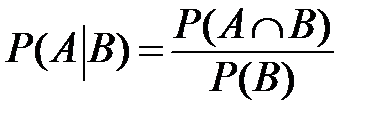 
. Рассмотренные нами случай несовместных событий и случай согласуются с данной формулой.
В случае равновероятных исходов опыта формула условной вероятности имеет вид 
, где 
– число исходов, благоприятных для события , и 
из них благоприятствуют событию .
Пример. Найти вероятность того, что при бросании игрального кубика выпало число 3, если известно, что выпавшее число нечетное.
Число исходов, благоприятных для выпадения нечетного числа, равно 3 (1, 3, 5). Из этих исходов только один благоприятен выпадению числа 3. Следовательно, искомая вероятность равна 
.
Проверим, чему равна условная вероятность 
, если события и независимы. Согласно определению вероятности пересечения независимых событий
. Этот результат, несомненно, соответствует интуитивному представлению о том, что если события и независимы, то на вероятность наступления события никак не влияет, произошло событие или не произошло.
Условная вероятность используется для вычисления вероятности наступления события при известных вероятностях исходов опыта и условных вероятностях наступления события при каждом исходе. Справедлива следующая теорема.
Пусть 
– множество исходов некоторого опыта (то есть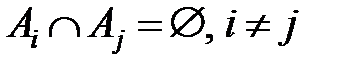 
, и 
). Тогда 
.
Последняя формула называется формулой полной вероятности.
Пример. По самолету производится три выстрела. Вероятность попадания при первом выстреле 0,5, при втором 0,6, при третьем 0,8. При одном попадании самолет будет сбит с вероятностью 0,3, при двух попаданиях с вероятностью 0,6, при трех самолет будет сбит наверняка. Какова вероятность того, что самолет будет сбит?
Событием 
является событие «самолет сбит». Множество исходов при трех выстрелах – это события: 
– «попадания при всех трех выстрелах», 
– «два попадания и один промах», 
– «одно попадание и два промаха», 
– «три промаха». Имеем 
, 
, 
, 
. Теперь нужно подсчитать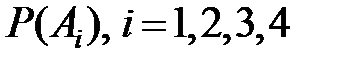 
. Используя независимость попаданий, получим 
. Событие 
– это объединение трех несовместных событий: «попадание при первых двух выстрелах и промах при третьем», «попадание при первом и третьем выстрелах и промах при втором» и «промах при первом выстреле и попадание при двух следующих». Поэтому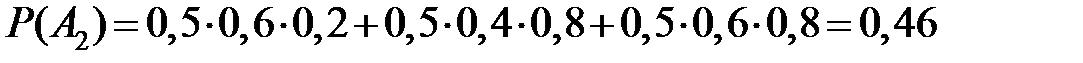 
.
Аналогично считается вероятность третьего исхода: 
. Очевидно, что в силу независимости промахов 
. В результате применения формулы полной вероятности получим 
.
Представим, что нас интересует не столько событие, происшедшее в результате опыта, а то, при каком исходе из множества всех исходов это событие произошло. Назовем при этом множество исходов множеством гипотез.
Пример. Одинаковыедетали производятся в трех цехах. В первом цехе 50% всех деталей, во втором цехе 30% и в третьем цехе 20%. Вероятность выпуска бракованной детали в 1-м цехе 0,02 во втором и третьем по 0,01 (видимо, там стоят более современные, чем в первом цехе, станки). К работникам ОТК попала бракованная деталь. Следует узнать вероятность того, что бракованная деталь из третьего цеха.
Итак, событием в данном опыте является событие 
– «появление бракованной детали». Гипотезами здесь являются исходы «деталь произведена в 1-м цехе», «деталь произведена во 2-м цехе» и «деталь произведена в 3-м цехе». Обозначим эти гипотезы 
, соответственно. Очевидна вероятность исходов-гипотез по объему поступающей из цехов продукции: 
.
Известны также вероятности события 
при каждой из гипотез: 
. Как же подсчитать 
? Ответ на этот вопрос дает теорема Байеса.
Пусть 
– полная группа событий. Тогда
.
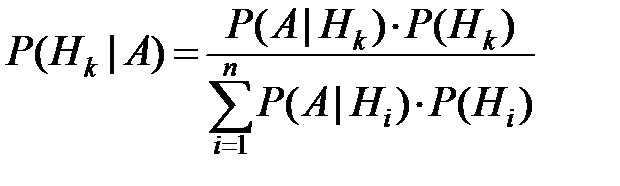Применяя теорему Байеса, решим поставленную в примере задачу: подсчитаем вероятность того, что бракованная деталь из третьего цеха. 
.
Многие задачи теории вероятностей сводятся к тому, что опыт проводится 
раз независимым образом, причем наступление события 
в одном опыте не влияет на наступление того же события в другом опыте. Если вероятность наступления события в одном опыте равна 
, то чему равна вероятность наступлений этого события 
раз при проведенных опытах (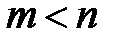
)?. Так как при проведении опытов событие произойдет раз и не произойдет 
раз, то если мы зафиксируем, в каких опытах событие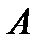 
произойдет, а в каких нет, из-за независимости наступления или отсутствия события мы должны получить 
. Но поскольку мы не знаем, в каких опытах событие произойдет, а в каких нет, мы должны просуммировать вероятности несовместных событий, отличающихся номерами опытов, в которых событие происходит. Число различных вариантов групп опытов с происшедшими событиями равно 
. Поэтому ответ на поставленный вопрос дает формула Бернулли: 
.
Пример. Какова вероятность того, что при десяти бросаниях игральной кости два раза выпадет 6? Здесь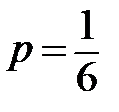 
, 
. Следовательно, вероятность интересующего нас события 
.
Заметим, что в соответствии с формулой бинома Ньютона сумма вероятностей наступления событий 0, 1, 2, …, раз при проведении опытов равна 1.
Задания.
1. В урне содержится 5 белых и 4 черных шара. 1) Вынимается наудачу один шар. Найти вероятность того, что он белый. 2) Вынимаются наудачу два шара. Найти вероятность того, что: а) оба шара белые; б) хотя бы один из них черный.
2. В коробке 5 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Найти вероятность того, что: а) все они одного цвета; б) все они разных цветов; в) среди них 2 синих и 1 зеленый карандаш.
3. Дано 6 карточек с буквами Н, М, И, Я, Л, О. Найти вероятность того, что: а) получится слово ЛОМ, если наугад одна за другой выбираются три карточки; б) получится слово МОЛНИЯ, если наугад одна за другой выбираются 6 карточек.
4. Брошены две игральные кости. Найти вероятность того, что: а) сумма выпавших очков не превосходит 7; б) на обеих костях выпадает одинаковое число очков; в) произведение выпавших очков делится на 4; г) хотя бы на одной кости выпадет 6 очков.
5. Код домофона состоит из 8 цифр, которые могут повторяться. Какова вероятность того, что случайно набирая цифры, можно угадать нужный код?
6. Наудачу взятый телефонный номер состоит из 6 цифр. Определить вероятность того, все 6 цифр различны.
7. Имеется 6 изделий: 4 из них первого сорта и 2 второго. Наудачу взяли 3 изделия. Найти вероятность того, что среди них только одно первого сорта.
8. Среди 12 студентов 7 отличников. Из группы отобрано наудачу 5 человек. Какова вероятность того, что среди них 3 отличника.
9. Среди 20 изделий 3 дефектных. Случайно из них отобрано 4 изделия. Найти вероятность того, что а) все отобранные годны; б) число годных и дефектных одинаково.
10. Каждый из двух стрелков делает по одному выстрелу в мишень. Пусть событие А – первый стрелок попал в цель, событие В – второй стрелок попал в цель. Что означают события: а) А + В; б) А 
В; в) 
.
11. Из корзины, содержащей красные, желтые и белые розы выбирается один цветок. Пусть события А – вынута красная роза, В – вынута желтая роза, С – вынута белая роза. Что означают события: а) В + С; б) А + В; в) А С; г) 
; д) А+В+С; е) А В + С?
12. Три студента независимо друг от друга решают задачу. Пусть событие А1 - первый студент решил задачу, событие А2 – второй студент решил задачу, А3 – третий студент решил задачу. Выразить через события Аi (i= 1,2,3) следующие события: 1) А – все студенты решили задачу; 2) В – задачу решил только первый студент; 3) С – задачу решил хотя бы один студент; 4) D – задачу решил только один студент; 5) Е – с задачей не справился ни один студент; 6) F – задачу решило не более двух студентов.
13. Только один из 9 ключей подходит к данному замку. Какова вероятность того, что придется опробовать 5 ключей для открывания замка?
14. При включении зажигания двигатель начинает работать с вероятностью 0,9. Какова вероятность того, что для запуска двигателя придется включать зажигание не более трех раз?
Случайные величины.
Случайной величиной называют функцию, заданную на множестве исходов конкретного опыта.
