Пусть А,В,С,…,Х,У,Z (прописные латинские буквы)– переменные, которыми мы будем обозначать элементарные высказывания. Такие переменные называются высказывательными или пропозиционными. Рассмотрим: символы логических операций 
(⌐), 
, Ú, →, ↔ и скобки для указывания порядка действий.
Из перечисленных элементов составляются формулы. Чтобы из повествовательного предложения получить формулу нужно
1) выделить все элементарные высказывания и логические операции, образующие данное предложение,
2) заменить их соответствующими буквами и символами,
3) в соответствии со смыслом предложения расставить скобки, установив порядок действий.
Примеры. 1. Предложение «Сдать зачет по математике можно, зная блестяще теорию или решив все примеры» можно представить так АÚВ, где А: «Сдать зачет можно, зная блестяще теорию», В: «Сдать зачет можно, решив все примеры»
2. Предложение «Если Сувар или Таиф проиграют, а Феникс выиграет тендер, то Альбатрос упрочит свое положение и мы понесем убытки» представляет собой импликацию А→В, где посылка А составлена из трех элементарных высказываний: Р: «Сувар проиграет», Q: «Таиф проиграет», R: «Феникс выиграет», а заключение В есть конъюнкция высказываний: D: «Альбатрос упрочит свое положение» и С: «Мы понесем убытки».С помощью введенных символов первоначальное предложение записывается в виде формулы: F: ((PÚ Q) 
R) → (D 
C).
Если истинностные значения простых переменных P, Q, R, D, C соответственно равны И, Л, Л, И, Л, то истинностное значение сложного высказывания F может быть определено механически, используя таблицы истинности логических операций, следующим образом
((PÚ Q) 
R) → (D 
C)
((ИÚЛ) 
Л) → (И 
Л)
(И 
Л) → Л
Л→ Л
И
Таким образом, при заданном наборе значений простых высказываний, используя аксиоматику логических операций, мы определяем значение высказывания, получаемого с помощью логической формулы.
Если дано сложное высказывание в виде логической формулы, то часто бывает важно знать, для какого набора значений переменных это сложное высказывание истинно, для какого ложно. Тогда, как и при доказательстве законов логики, применяют таблицы истинности, в которых дается перебор всех возможных комбинаций значений простых высказываний, из которых состоит логическая формула, и получение соответствующих значений сложного высказывания.
Пример. Доказать, что при любых значениях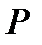 
и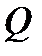 
справедлива формула 
.
| 
| 
| 
| 
| 
|
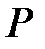
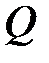
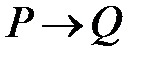
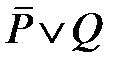
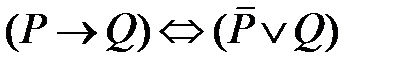
| И | И | И | Л | И | И |
| И | Л | Л | Л | Л | И |
| Л | И | И | И | И | И |
| Л | Л | И | И | И | И |
Высказывание, истинное при любых значениях входящих в нее простых высказываний, называется тавтологией.
В случае, когда логическая формула содержит булевы операции, доказательства тавтологий или упрощение формул проще проводить, не строя таблицы истинности, а применяя доказанные нами основные законы логики высказываний.
Пример. Доказать тавтологию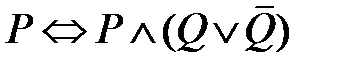 
.
Согласно закону 14 правая часть эквиваленции имеет вид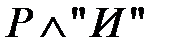 
, Применяем вторую часть закона 16, тогда правая часть превращается в 
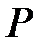. Поскольку любое высказывание равносильно самому себе, тавтология доказана.
Пример. Упростить высказывание 
.
Последовательно применяя законы, имеем: 
= = 
= 
= 
= 
= 
= 
= 
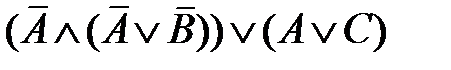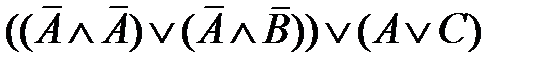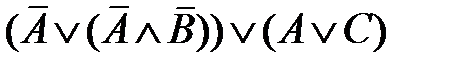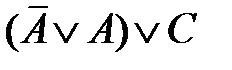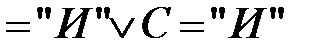. Таким образом, исходное высказывание – тавтология.
Пример. Доказать, что справедлива формула 
.
= 
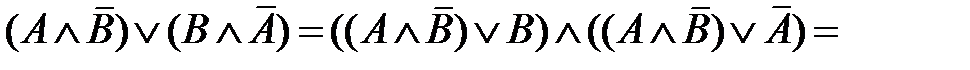
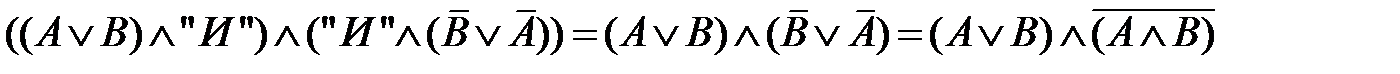, что и требовалось доказать.
