Общая задача нелинейного программирования

 

Во многих экономических моделях зависимости между постоянными и переменными факторами лишь в первом приближении можно считать линейными, более детальное рассмотрение позволяет обнаружить их нелинейность. Как правило, такие показатели, как прибыль, себестоимость, капитальные затраты на производство и др., в действительности зависящие от объема производства, расхода ресурсов и т.п., не линейны.

Общая оптимизационная задача формулируется следующим образом: найти вектор X=(x₁,x₂,..., x_n), удовлетворяющий системе ограничений, представляемых в виде совокупности равенств и/или неравенств вида

j_i(x₁, x₂,..., x_n) £ b_i, i=1,2,...,k, (1)

j_i(x₁, x₂,..., x_n) = b_i, i=k+1,k+2,...,m

и доставляющий экстремальное значение целевой функции

Z=f(x₁, x₂,..., x_n); (2)

При этом на некоторые переменные x₁, x₂,..., x_n могут накладываться условия неотрицательности и целочисленности.

В случае если одна из функций j_i и/или f будет нелинейной, то полученную модель считают задачей нелинейного программирования (ЗНП). Класс ЗНП шире класса ЗЛП. Основные результаты получены при рассмотрении задач, в которых ограничения имеют линейный вид, а целевая функция нелинейная. Рассмотрим частные случаи, когда целевая функция сепарабельная (ее можно представить в виде суммы функций, каждая из которых зависит от одной переменной) или квадратичная.

С помощью большинства вычислительных методов можно найти точку локального оптимума, но нельзя установить, является ли она точкой глобального (абсолютного) оптимума или нет. Если задача содержит нелинейные ограничения, то область допустимых решений не является выпуклой и кроме глобального оптимума могут существовать точки локального оптимума.

Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. Рассмотрение ЗНП начинают с классической задачи оптимизации. Задачи такого рода имеют место, если система (1) содержит только уравнения, отсутствуют условия неотрицательности и целочисленности переменных, а функции j_i(x₁, x₂,..., x_n) и f(x₁, x₂,..., x_n) непрерывны и имеют частные производные не ниже второго порядка. Т.е. задачу оптимизации можно сформулировать так: найти переменные x₁, x₂,..., x_n, удовлетворяющие системе уравнений

j_i (x₁, x₂,..., x_n) = b_i, i=1,2,...,m, (3)

и обращающие в максимум (минимум) целевую функцию

Z=f(x₁, x₂,..., x_n). (4)

Примером типичной и простой ЗНП является следующая: данное предприятие для производства какого-то продукта расходует два средства в количестве х₁ и х₂. Это факторы производства, например, машины и труд, а величины х₁ и х₂ – затраты факторов производства. Объем производства (выраженный в натуральных или стоимостных единицах) является функцией затрат производства Z=f(x₁, x₂). Эта зависимость называется производственной функцией. Издержки зависят от расхода обоих факторов (x₁ и x₂) и от цен этих факторов (с₁ и с₂). Совокупные издержки выражаются формулой b=c₁x₁+c₂x₂. Требуется при данных совокупных издержках определить такое количество факторов производства, которое максимизирует объем продукции Z.

Математическая модель этой задачи: найти переменные x₁, x₂, удовлетворяющие условиям b=c₁x₁+c₂x₂, х₁³0, х₂³0, при которых функция Z=f(x₁, x₂) достигает максимума. Как правило, функция Z может иметь произвольный нелинейный вид.

Максимум и минимум функции объединяется понятием экстремум, который может быть локальным или глобальным.

Используя классические методы оптимизации, следует четко представлять себе различие между локальным экстремумом функции, глобальным экстремумом и условным экстремумом.

Будем полагать, что функция Z=f(x₁, x₂,..., x_n)= f(Х) дважды дифференцируема в точке Х*=(x*₁, x*₂,..., x*_n) и в некоторой ее окрестности. Если для всех точек Х этой окрестности f(Х*)³ f(Х) или f(Х*)£ f(Х), то говорят, что функция f(Х) имеет локальный экстремум в Х* (соответственно максимум или минимум).

Точка Х*, в которой все частные производные функции f(Х) равны 0, называется стационарной точкой.

Необходимое условие экстремума: если в точке Х* функция f(Х) имеет экстремум, то частные производные функции в этой точке равны нулю:

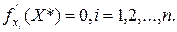
Как правило, в практических задачах необходимо определить наибольшее и наименьшее значение функции (глобальный экстремум) в некоторой области.

Функция Z=f(Х) имеет в точке Х* заданной области D глобальный максимум (наибольшее значение) или глобальный минимум (наименьшее значение), если неравенство f(Х*)³ f(Х) или f(Х*)£ f(Х) соответственно выполняется для любой точки

ХÎ D.

Если область D замкнута и ограничена, то дифференцируемая функция Z=f(Х) достигает в этой области своих наибольшего и наименьшего значений в стационарной точке или в граничной точке области (теорема Вейерштрасса).

Следовательно, чтобы найти наибольшее (наименьшее) значение функции Z=f(Х) в области D, нужно:

1) найти все стационарные точки внутри области D и вычислить значения функции в них;

2) исследовать функцию на экстремум на границе области D;

3) сравнить значения функции, полученные в п.1 и 2: наибольшее (наименьшее) из этих чисел и будет наибольшим (наименьшим) значением функции в этой области.

Граница области D аналитически может быть задана системой уравнений (условий) относительно переменных x₁, x₂,..., x_n. Поэтому, исследуя экстремальные свойства функции на границе, необходимо решить задачу определения условного экстремума.

Пусть необходимо найти экстремум функции Z=f(x₁, x₂,..., x_n) при условии, что переменных x₁, x₂,..., x_n удовлетворяют уравнениям

j_i(x₁, x₂,..., x_n) = 0, i=1,2,...,m, m<n. (*)

Предполагается, что функции f и j_i имеют непрерывные частные производные по всем переменным. Уравнения (*) называют уравнениями связи.

Функция Z=f(Х) имеет в точке 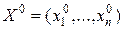, удовлетворяющей уравнениям связи (*), условный максимум (минимум), если неравенство f(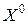)³ f(Х) (f(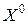)£ f(Х)) имеет место для всех точек Х, координаты которых удовлетворяют уравнениям связи.

Легко заметить, что задача определения условного экстремума совпадает с ЗНП (3), (4).

Один из способов определения условного экстремума применяется в том случае, если из уравнений связи m переменных можно явно выразить через оставшиеся n-m переменных:

x_i=y_I(x_m+1, …,x_n), i=1,2,…,m.

Подставив полученные выражения для x_i в функцию Z, получим

Z= f(y₁(x_m+1, …,x_n),…, y_m(x_m+1, …,x_n), x_m+1, …,x_n), или Z=F(x_m+1, …,x_n).

Задача сведена к нахождению локального (глобального) экстремума для функции

n-m переменных. Если в точке 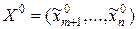функция Z=F(x_m+1, …,x_n) имеет экстремум, то в точке 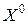=(y₁ ,…,y_m , 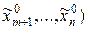функция Z=f(x₁, x₂,..., x_n) имеет условный экстремум (сформулированный ранее).

 

Если число переменных n=2, нелинейные задачи можно решить графически. Ограничения должны быть записаны в виде неравенств j_i(x₁, x₂,..., x_n) £ b_i, i=1,2,...,m, а целевая функция иметь вид Z=f(x₁, x₂).

Как и в случаегеометрического решения ЗЛП, сначала необходимо построить область допустимых решение (ОДР) – множество точек плоскости, удовлетворяющих неравенствам j_i(x₁, x₂,..., x_n) £ b_i. Но в отличии от ЗЛП здесь ОДР не обязательно будет выпуклой и может быть разрывной. Экстремум функции может достигаться и внутри области, и на границе.

После построения ОДР следует записать уравнения линий уровня целевой функции- множество точек плоскости, в которых целевая функция постоянна: f(x₁, x₂)=C, и определить направление возрастания (убывания) целевой функции, построив, например, линии уровня для разных значений С. Затем, перемещая линию уровня в нужном направлении в ОДР, найти точки области, в которых целевая функция принимает оптимальное значение.

Пример1. Найти минимальное и максимальное значения сепарабельной функции Z=(x₁-4)²+(x₂-6)² при ограничениях:

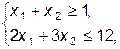x₁³0, x₂³0.

Решение. ОДР представляет собой многоугольник ABCE (рис. 1). Если положить Z=Q (Q>0),то линии уровня целевой функции - это уравнение окружности (x₁-4)²+(x₂-6)²=Q. С уменьшением (увеличением) Q (квадрата радиуса) значения функции Z соответственно уменьшаются (увеличиваются).

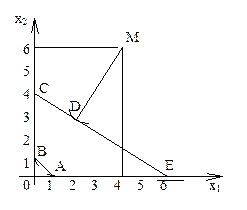
Центром окружностей будет точка М с координатами (4, 6). Проведем из точки M окружности различных радиусов при разных Q и получим: минимальное значение функция Z(D)=196/13 принимает в точке D (24/13,36/13), в которой окружность касается области решений. Точка D не является угловой, ее координаты находят в результате решения системы уравнений, соответствующих прямым MD и CE.

Функция Z имеет два локальных максимума: в вершине A(1;0) функция

Рис.1 Z(A)=45, в вершине E(6;0) функция Z(e)=40.

Так как Z(А)>Z(E), то вершина A является точкой глобального максимума.

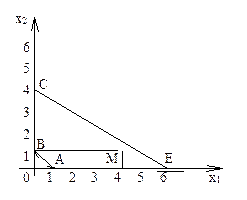
Пример 2. Пусть область допустимых решений остается прежней, а
Z=(x₁-4)²+(x₂-1)². Найти минимальное и максимальное значения этой функции.

Решение. Минимальное значение функция принимает в точке M(4;1) (рис.2): Z(M)=0. Функция Z имеет два локальных максимума: в вершине E(6;0) функция Z(E)=5, в вершине С(0;4) функция Z(C)=25, причем глобальный максимум достигается в вершине С.

Рис. 2

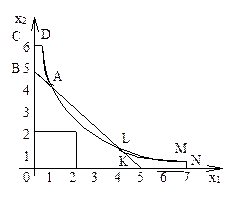
Пример 3. Найти минимальное и максимальное значения функции Z=x₁²+x₂² при ограничениях

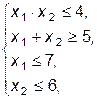x₁³0, x₂³0.

Решение. В этом случае (рис.3) область допустимых решений не является выпуклой и состоит из двух отдельных частей. Минимальное значение функции Z=17 достигается в точках A(1;4) и L(4;1). Функция Z

Рис.3. имеет два локальных максимума: в точке
D(2/3; 6) функция Z(D)=328/9 и в точке M(7; 4/7) функция Z(M)=2417/49. Точка M является точкой глобального максимума.

 

Метод множителей Лагранжа

 

Выразить в явном виде из уравнений связи (условий-ограничений) необходимую часть переменных, как правило, не удается. Французский математик и механик Лагранж предложил оригинальный метод нахождения условного экстремума функции в данном случае, который носит его имя.

Пусть задана задача математического программирования: максимизировать функцию

f(x₁,x₂,...,x_n) (5)

при ограничениях

j_j(x₁,x₂,...,x_n)=0, j=1,2,...,m, m<n. (6)

Ограничения в задаче заданы уравнениями. Полагаем, что функции f и j_i имеют непрерывные частные производные по всем переменным. Для решения задачи составим функцию:

L(x₁,x₂,...,x_n,l₁,l₂,...,l_m)=f(x₁,x₂,...,x_{n)+ 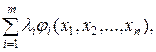.} (7)

которая называется функцией Лагранжа, а числа l_i - множителями Лагранжа. Отметим, что множителям Лагранжа можно придать экономический смысл. Если f(x₁,x₂,...,x_n) – доход, соответствующий плану Х=(x₁,x₂,...,x_n), а функция j_j(x₁,x₂,...,x_n) – издержки i-го ресурса, соответствующие этому плану, то l_i – цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса (маргинальная оценка).

Обозначим через X совокупность переменных x_j (j=1,2,...,n), а через L - совокупность переменных множителей l_i (i=1,2,...,m). Определим частные производные 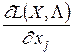(j=1,2,...,n), 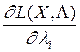(i=1,2,...,m) и приравняем их к нулю. В результате получим систему уравнений:

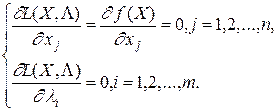(8)

Легко заметить, что 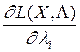=j_j(Х), т.е. в (8) входять уравнения связи.

Если функция Z=f(x₁,x₂,...,x_n) в точке X^(o)=(x₁^(o), x₂^(o),..., x_n^(o)) имеет экстремум, то существует такой вектор L^(o)=(l₁^(o),l₂^(o),...,l_m^(o)), что точка
(x₁^(o), x₂^(o),..., x_n^(o), l₁^(o), l₂^(o),..., l_m^(o)) является решением системы (8). Следовательно, нахождение условного экстремума функции Z=f(Х) сводится к нахождению локального экстремума функции L(X,L). При этом неизвестен способ определения точек глобального минимума или максимума. Однако если решения системы найдены, то для определения глобального максимума (минимума) достаточно найти значения функции в соответствующих точках. Если для функций Z=f(x₁,x₂,...,x_n) и j_i(x₁,x₂,...,x_n) (i=1,2,...,m) существуют вторые частные производные и они непрерывны, то можно вывести достаточное условие существования локального экстремума функции в точке, являющейся решением системы (8). Однако практическое значение этого условия невелико.

Метод множителей Лагранжа имеет ограниченное применение, так как система (8), как правило, имеет несколько решений.

Пример 4. Найти точку условного экстремума функции Z=x₁x₂+x₂x₃ при ограничениях .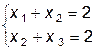

Решение. Составим функцию Лагранжа L(x₁,x₂,x₃,l₁,l₂)= x₁x₂+x₂x₃+l₁(x₁+x₂-2)+ l₂(x₂+x₃-2) и продифференцируем ее по переменным x₁, x₂, x₃, l₁ и l₂. Приравнивая полученные выражения нулю, получим следующую систему уравнений:

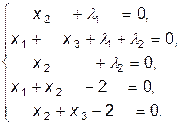
Из первого и третьего уравнения следует, что l₁=l₂=-x₂; тогда

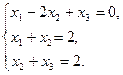
Решая данную систему, получим x₁=x₂=x₃=1; Z=2.

 

9.3. Обобщёние метода множителей Лагранжа

Метод Лагранжа теоретически можно использовать и когда ограничения имеют вид неравенств и их решения должны быть неотрицательными.

Пусть задана задача математического программирования: максимизировать функцию

Z=f(x₁,x₂,...,x_n) (5)

при ограничениях

j_j(x₁,x₂,...,x_n)=0, j=1,2,...,m, m<n. (6)

Рассмотрим ситуацию, когда к основным ограничениям-равенствам, исходной задачи добавлены ограничения x_j ³ 0, j=1, 2,...,n, т.е. введено условие неотрицательности.

Функция f(Х) может принимать экстремальное значение как на границе x_j ³ 0, так и внутри ее области.

На первом этапе находят неотрицательные решения X⁰=(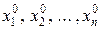) системы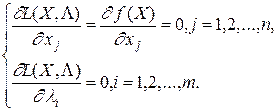

и определяют значения Z, принадлежащих области изменения переменных.

Если экстремум f(x) располагается в граничной точке, то последовательно рассматривают случаи, когда одна из переменных обращается в 0, т.е. решают последовательно n задач с n-1 переменной и m ограничениями, получаемых в результате поочерёдных подстановок нулевых значений координат x₁=0, x₂=0,..., x_n=0 в выражения f(x₁,x₂,...,x_n) и j_i(x₁,x₂,...,x_n) (i=1, 2,..., m). Решив n таких задач, приравнивают 0 две переменные и решаются C_n² задач с n-2 переменными и m ограничениями т. д.

На последнем шаге приравнивают 0 n-m переменных, тем самым однозначно оставшиеся m переменных. Для этих значений также вычисляют значения Z. Отметим, что приравнивать нулю можно одновременно не более, чем n-m координат, т. е. число ограничений не должно превышать числа переменных.

Определив подобным образом все граничные точки, которым соответствуют экстремальные значения и стационарные внутренние точки функции f(x), вычисляют значения целевой функции в этих точках и сравнивают их между собой, выбирая наибольшее или наименьшее значение, которое принимается за искомое экстремальное f(x^*). Однако при достаточно большом числе переменных трудности в вычислениях могут оказаться непреодолимыми.

Требование неотрицательности x_j³0 может накладываться не на все координаты X=(x₁,x₂,...,x_n), а только на часть переменных, тогда соответствующие комбинации с нулевыми переменными в выше описанной процедуре допускаются только из тех переменных, которые должны удовлетворять этому требованию.

Теперь рассмотрим ситуацию, когда к системе ограничений-равенств добавляются ограничения, имеющие вид неравенств, т.е. имеем ограничения:

j_i(X)=j_i(x₁, x₂,..., x_n) £ b_i i=1,2,...,p;

j_i(X)=j_i(x₁,x₂,..., x_n)³b_i i=p+1,p+2,..., q;

g_i(X)=b_i i=q+1, q+2,..., m.

Пусть условие неотрицательности переменных снято. Наличие этого условия приводит, как было показано выше, к решению ряда промежуточных задач, делая более громоздким процедуру отыскания искомого экстремального решения.

Перепишем рассматриваемую систему ограничений в виде равенств, вводя для этого в неравенства новые переменные, которым предъявляем требования неотрицательности. В результате система ограничений принимает следующий вид:

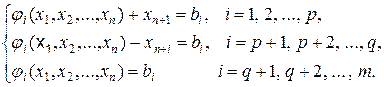
x_n+i ³ 0, i = 1, 2,..., q.

Такое представление ограничений даёт возможность воспользоваться ранее описанной процедурой нахождения экстремального значения целевой функции z=f(X) с ограничениями-равенствами и с условием неотрицательности для части переменных x_n+i, i=1, 2,..., q, которые к тому же не входят в выражение целевой функции.

Исследование данной задачи естественно начать с поиска возможного решения внутри области x_n+i³0, i=1, 2,..., q.

 

Теорема Куна-Таккера

 

Описанный подход обобщения метода множителей Лагранжа связан с необходимостью решения большого числа промежуточных задач при определении экстремального значения целевой функции. Однако если функция Лагранжа 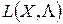в точке глобального экстремума исходной функции f(Х) имеет особенность, так называемую седловую точку, то схема обобщения метода множителей Лагранжа принимает более простую форму.

Седловой точкой для функции Лагранжа 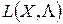( локальной седловой точкой ) называется точка 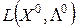=(x₁^(o), x₂^(o),..., x_n^(o), l₁^(o), l₂^(o),..., l_m^(o)), для которой для всех Х из e-окрестности точки 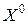и всех 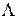из e-окрестности точки 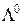будут выполняться неравенства L(X, L^(o)) £ L(X^(o), L^(o)) £ L(X^(o), L).

Точка 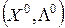определена как точка максимума функции Лагранжа 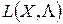по Х и минимума L по .

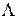Если неравенство L(X, L^(o)) £ L(X^(o), L^(o)) £ L(X^(o), L) выполняется для любых Х и 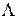, то точка 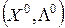является глобальной седловой точкой.

Центральное место в теории нелинейного программирования занимает теорема Куна-Таккера, которая устанавливает связь между условиями существования в точке 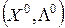глобальной седловой точки функции Лагранжа 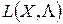и необходимыми и достаточными условиями, которым должна удовлетворять точка X⁰=(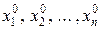), в которой целевая функция f(Х) достигает абсолютного условного экстремума.

Пусть дана ЗНП: найти максимальное значение функции Z=f(x₁,x₂,...,x_n) при ограничениях

j_i (x₁,x₂,...,x_n)=0, i=1,2,...,m,

x₁, x₂,...,x_n ³ 0 (9)

Составим функцию Лагранжа для данной задачи:

L(X,L)=f(X) + 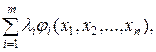(10)

Если выполняется условие регулярности (существует по крайней мере одна точка X, для которой j_i (X)>0 для всех i), то имеет место следующая теорема.

Теорема Куна-Таккера. Вектор X^(o) тогда и только тогда является оптимальным решением задачи (9), когда существует такой вектор L^(o), что при X^(o) ³ 0 и L^(o) ³ 0 для всех
X ³ 0 и L ³ 0

L(X, L^(o)) £ L(X^(o), L^(o)) £ L(X^(o), L). (11)

Теорема также называется теоремой о седловой точке.

Доказательство достаточности условий (11). Пусть X^(o) > 0 и L^(o) > 0 - седловая точка функции L(X, L). Если в (11) вместо L(X, L) подставить ее значение (10), то получим

f(X)+ 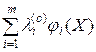£f(X^(o))+ 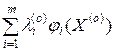£f(X^(o))+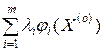

при X ³ 0, L ³ 0.

Правое неравенство справедливо при любом L ³ 0, поэтому

j_i (X) ³ 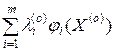0, =0.

Тогда из левого неравенства получим

f(X^(o)) ³ f(X)+ 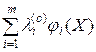при X ³ 0.

Так как при этом 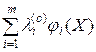³ 0, то f(X^(o)) ³ f(X).

Таким образом, точка X^(o) удовлетворяет ограничениям (11) и во всех других точках функция принимает значение меньшее, чем в X^(o). Это утверждение приводит решение задачи к отысканию седловых точек функции Лагранжа L(X,L).

Доказательство необходимости условий (11) ввиду его сложности не рассматривается.

Если f(X) и j_i(X) - дифференцируемые функции, то (11) эквивалентны следующим локальным условиям Куна-Таккера:

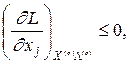(12)

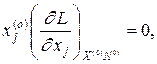
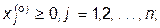
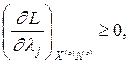(13)

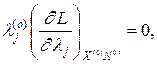
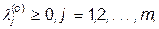
Выражение 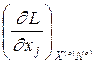означает, что значение частной производной функции Лагранжа берется в точке (X^(o), L^(o)), где X^(o)=(x₁^(o), x₂^(o),..., x_n^(o)),
L^(o)=(l₁^(o), l₂^(o),..., l_m^(o)).

Пример. Найти max Z = -x₁² -x₂² при ограничениях

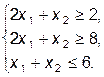x₁³0, x₂³0.

Решение. С помощью графического метода легко решить данную задачу: x₁=0,8, x₂=0,4, Z= -0,8.

Покажем, что существует L^(o) ³ 0, при котором в точке оптимума выполняются условия Куна-Таккера (12), (13) для функции F(X, L):

F(X, L)=-x₁²-x₂²+l₁(2x₁+x₂-2)+l₂(8-2x₁-x₂)+l₃(6-x₁-x₂).

Находим:

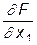= -2x₁+2l₁-l₃; 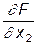= -2x₂+l₁-l₂-l₃;

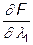=2x₁+x₂-2; 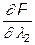=8-2x₁-x₂; 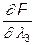=6-x₁-x₂.

Согласно условиям (13) l₂ и l₃ должны принимать нулевые значения, так, как, подставляя x₁=0,8 и x₂=0,4 в выражения 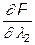и 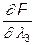, имеем значения, большие нуля, а по условию, 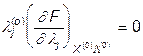. Согласно условию l₁ может принимать ненулевое значение, так как 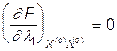. В соответствии с (12) производная 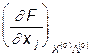(j=1,2) должна принимать ненулевые значения, так как координаты вектора X^(o) отличны от нуля. Находим l₁=0,8. Следовательно, в точке (X^(o), L^(o)) выполняются условия Куна-Таккера и она действительно является точкой экстремума.