Геометрическая интерпретация игры 2 х 2

Решение игры 2´2 допускает наглядную геометрическую интерпретацию.

Пусть игра задана платежной матрицей Р=(a_ij), i,j=1,2. На оси абсцисс отложим единичный отрезок А₁А₂. Левый конец отрезка - точка А₁ (x=0) соответствует стратегии A₁, правый стратегии A₂. Все промежуточные точки х этого отрезка соответствуют некоторым смешанным стратегиям S_A 1-го игрока, где р₁=1-x, р₂=x. На концах выбранного отрезка проведем прямые, перпендикулярные оси абсцисс, на них будем откладывать выигрыши при соответствующих чистых стратегиях А₁ и А₂. Если игрок B применяет стратегию B₁, то выигрыш при использовании чистых стратегий A₁ и A₂ составляет соответственно a₁₁ и a₂₁. Отложим эти точки на прямых и соединим полученные точки прямой B₁B₁. Средний выигрыш n₁, соответствующий смешанной стратегии S_A, определяется по формуле математического ожидания и равен ординате точки M₁, лежащей на прямой B₁B₁ (рис. 1).

Таким образом, если игрок А применяет смешанную стратегию, то его выигрышу соответствует некоторая точка М, лежащая на этой прямой.

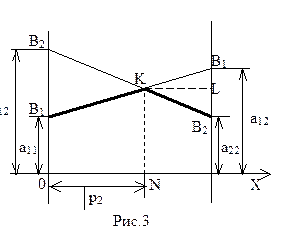Аналогично можно построить отрезок B₂B₂, соответствующий стратегии B₂ игрока B (рис. 2). При этом средний выигрыш 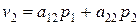- ордината точки M_2.

В соответствии с принципом минимакса оптимальная стратегия S*_A такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной B₁KB₂ (рис. 3), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке В₁К – против стратегии В₁, на участке КВ₂ - против стратегии В₂). Т.о., ломаная B₁KB₂ является нижней границей выигрыша, получаемого игроком A. Оптимальную стратегию S*_A=(р*₁,р*₂) определяет точка K с координатами (x,y), в которой минимальный выигрыш достигает максимума, ее ордината равна цене игры: y= v, абсцисса х= р*₁.

Чтобы найти координаты точки К, найдем уравнения прямых В₁В₁ и В₂В₂, на пересечении которых она лежит. Прямая В₁В₁ проходит через точки (0,а₁₁) и (1,а₁₂), подставив эти точки поочередно в общий вид уравнения прямой y=kx+b, получим ее уравнение y=k₁x+b₁. Аналогично, прямая В₂В₂ проходит через точки (0,а₂₁) и (1,а₂₂), получим ее уравнение y=k₂x+b₂. Решив систему получим координаты точки К х и y. Тогда, р*₁=х, р*₂=1-х и

v =y.

Используя геометрическую интерпретацию, можно найти решение игр 2´n. Каждой из n стратегий игрока B соответствует прямая. Построив эти прямые, находят нижнюю границу выигрыша. Точка K, лежащая на нижней границе, для которой величина выигрыша наибольшая, определяет цену игры и ее решение. При этом определяются активные стратегии игрока B (соответствующие им прямые пересекаются в точке K); из геометрических соображений можно найти значения q_j, соответствующие активным стратегиям игрока B.

Аналогично может быть решена игра m´2, только в этом случае строят верхнюю границу выигрыша и на ней определяют минимум.

Следует отметить, что геометрические построения имеет смысл использовать для определения активных стратегий игроков. Затем решение игры можно получить с помощью формул (3) – (5), или соответствующие значения S_A, S_B и v находят из геометрических соображений. Формулы (3) – (5) можно использовать, так как из соответствующей матрицы исключаются все стратегии, кроме активных, и она содержит две строки и два столбца.

Пример 4. Предприятие может выпускать два вида продукции А₁ и А₂, получая при этом прибыль, зависящую от спроса, который может быть в одном из 4-х состояний В₁, В₂, В₃, в₄. Дана матрица

A = , элементы которой a_ij характеризуют прибыль, которую получит предприятие при выпуске i-ой продукции с j-м состоянием спроса.

Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.

Решение. Задача сводится к игровой модели, в которой игра предприятия А против спроса В задана платежной матрицей А.

Определяем верхнюю и нижнюю цены игры и проверяем, имеет ли игра седловую точку.

Нижняя цена игры .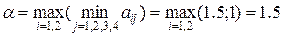

Верхняя ценя игры . Седловая точка отсутствует. Решение игры S*_A= (р₁^*,р₂^*), S*_B= (q₁^*, q₂^*, q₃^*, q₄^*) и n следует искать в смешанных стратегиях.

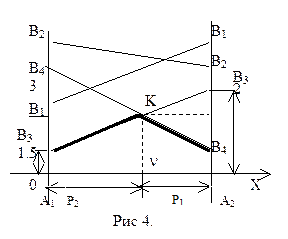
Откладываем на оси абсцисс (рис.4) единичный отрезок А₁А₂ . На левой вертикальной оси откладываем отрезки а₁₁=2, а₁₂=4, а₁₃=1.5, а₁₄=3, соответствующие стратегиям В₁, В₂, В₃, В₄. На правой вертикальной оси откладываем отрезки а₂₁=4, а₂₂=3, а₂₃=2, а₂₄=1, соответствующие тем же стратегиям В₁, В₂, В₃, В₄. Ломаная B₃KB₄ соответствует нижней границе выигрыша. Активные стратегии игрока B – третья и четвертая, тогда q₁^*=0, q₂^*=0. Следовательно платежную матрицу можно упростить: A = .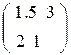

Ломаная B₃KB₄ является нижней границей выигрыша, получаемого игроком A. Оптимальную стратегию S*_A=(р*₁,р*₂) определяют точка K с координатами (x,y). Ее ордината y равна цене игры: y= v, абсцисса х= р*₁.

Чтобы найти координаты точки К, найдем уравнения прямых В₃В₃ и В₄В₄, на пересечении которых она лежит. Прямая В₃В₃ проходит через точки (0;1) и (1;2), подставив эти точки поочередно в общий вид уравнения прямой y=kx+b, получим ее уравнение y=0.5x+1.5. Аналогично, прямая В₄В₄ проходит через точки (0;3) и (1;1), получим ее уравнение y=-2x+3. Решив систему 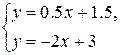получим координаты точки К х=0.6 и y=1.8. Тогда, р*₂=х=0.6, р*₁=1-х=0.4 и v =y=1.8.

Следовательно, S*_A = (0,4; 0,6), т.е. игрок A применяет стратегию A₁ c вероятностью 0,4, а стратегию A₂ – с вероятностью 0,6. При этом его выигрыш в среднем составит v=1,8 ед.

Оптимальные стратегии игрока В найдем с помощью формул (3)-(5). Запишем систему уравнений 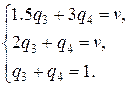Т.к. цена игры нами уже найдена v=1,8, то систему можно упростить: Решив систему, получаем оптимальную стратегию спроса В S*_B= (0, 0, 0.8,0.2)

С экономической точки зрения можно сделать вывод, что предприятие должно выпустить 40% продукции А₁ и 60% продукции А₂. А оптимальный спрос в 80% находится в состоянии В₃ и в 20% - в состоянии В₄.

Пример 5. Найти решение игры, заданной матрицей A = .

Решение. Матрица имеет размерность 2´4. На рис. 5 построены прямые, соответствующие стратегиям игрока A. Жирной линией на рис. 5 изображена верхняя граница выигрыша игрока A.

Найдя верхнюю и нижнюю цену игры, определяем, что игра без седловой точки.

Точка K определяет цену игры. Активными стратегиями для игрока A являются первая и четвертая. Следовательно, платежную матрицу можно упростить: A = 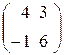. Стратегию S*_B= (q₁, q₂) и цену игры v находим геометрическим способом, найдя уравнения прямых А₁А₁ и А₄А₄ (см. пример 4) и определив координаты точки К. Получаем S*_B =(3/8; 5/8); v=27/8. Стратегию S*_A=(р*₁,р*₂, р*₃, р*₄)= (р*₁, 0, 0, р*₄) найдем по формулам (3)-(5): S*_A =(7/8;0; 0; 1/8).