Игра mxn в общем случае не имеет геометрической интерпретации. Ее решение трудоемко при больших m и n, однако трудностей не имеет, так как может быть сведено к решению ЗЛП.
Пусть игра mxn задана платежной матрицей Р=(aij) i=1,2,…,m; j=1,2,…,n. которой имеет размерность m´n. Игрок А располагает стратегиями Ai, (i=1,2,...,m), а игрок В - стратегиями Вj, (j= 1, 2,..., n). Необходимо определить оптимальные стратегии S*A= (р1*,р2*, …, рm*) и S*B= (q1*, q2*,...,qn*), где рi* и qj* - вероятности применения соответствующих чистых стратегий Аi и Вj.
р1*+р2*+ …+ рm*=1, q1*+ q2*+...+qn*=1.
Применение игроком А оптимальной стратегии S*A должно обеспечить ему при любых действиях игрока В средний выигрыш не меньше цены игры v, т. е. необходимо выполнение соотношения 
j=1, 2,..., n. Цена игры неизвестна, но полагаем v>0, этого можно добиться, сделав все элементы aij³0, прибавляя ко всем aij некоторое положительное число, величина которого равна абсолютному значению элемента, наименьшего среди всех отрицательных элементов матрицы.
Если игрок А применяет смешанную стратегию S*A= (р1*,р2*, …, рm*) против любой чистой стратегии игрока В, то он получает средний выигрыш, или математическое ожидание выигрыша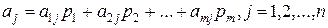 
(т.е. элементы j-го столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий А1,А2,…,Аm и результаты складываются).
Для оптимальной стратегии S*A все средние выигрыши не меньше цены игры, поэтому получаем систему неравенств 
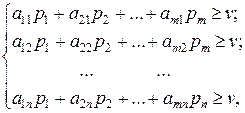(1)
Каждое из неравенств разделим на число v>0 и введем новые переменные 
(2)
Тогда система примет вид:
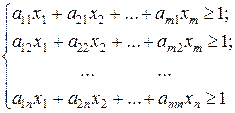(3)
Цель игрока А – максимизировать свой гарантированный выигрыш, т.е. цену игры.
Разделив на v>0 равенство р1+р2+ …+ рm=1, получаем, что переменные xi (i=1,2,..,m) удовлетворяют условию х1+х2+ …+ хm=1/v. Максимизация цены игры v эквивалентна минимизации величины 1/v, поэтому задача может быть сформулирована следующим образом: определить значения переменных xi³0 так, чтобы они удовлетворяли линейным ограничениям (3) и при этом линейная функция 
обращалась в минимум. Это ЗЛП. Решая задачу, находим значения xi и величину 1/v, затем получаем оптимальное решение рi*= vxi (I=1,2,..,m) и оптимальную стратегию S*A.
Для определения оптимальной стратегии S*B= (q1*, q2*,...,qn*) следует учесть, что игрок В стремится минимизировать гарантированный выигрыш, т.е. найти 
. Стратегия S*B должна обеспечить при любых стратегиях игрока А проигрыш, не превышающий величину v, т. е. необходимо выполнение соотношения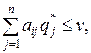 
i=1, 2,...,m, т.е. переменные q1, q2,...,qn удовлетворяют неравенствам
Если обозначить yj= 
j=1, 2,...,n, то получим
(4)
Элементы смешанных стратегий должны удовлетворять условиям
q1+q2+... +qn=1.
Данные условия в новых переменных (qj=yjv, j=1, 2,..., n) получают следующий вид:
y1+y2+... +yn= 
.
Игра свелась к ЗЛП: определить значения переменных y i³0, которые удовлетворяют линейным ограничениям (4) и максимизируют функцию 
.
Решая задачу, находим значения y i и величину 1/v, затем получаем оптимальное решение qj*= vyj (j=1,2,..,n) и оптимальную стратегию S*B.
Составив расширенные матрицы для задач, убеждаемся, что одна матрица получилась из другой транспонированием:
Таким образом, полученные для игроков А и В ЗЛП образуют симметричную пару двойственных задач. Свойство симметричности позволяет решать ту задачу, которая требует меньше вычислительных затрат, а решение второй задачи определяют на основании теорем двойственности. Очевидно, что искомая оптимальная цена игры для обеих игроков будет отыскиваться в следующем виде:
.
При решении произвольной конечной игры размера mxn рекомендуется придерживаться следующей схемы:
1. Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами, заведомо меньшими (большими) по сравнению с элементами других строк (столбцов).
2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если она есть, то соответствующие ей стратегии игроков будут оптимальными, а цена совпадает с верхней (нижней) ценой.
3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера 2х2, 2xn, nx2 возможно геометрическое решение.
Пример 6. Магазин может завести в разных пропорциях товары трех типов (А1, А2, А3). Их реализация и прибыль магазина зависят от вида товара и состояния спроса.
Предполагается, что спрос может иметь 3 состояния (В1, В2, В3) и не прогнозируется. Определить оптимальные пропорции в запуске товаров из условия максимизации средней гарантированной прибыли при следующей матрице прибыли
Р = 
.
Решение. Определим нижнюю и верхнюю цену игры: a=max{3;2;4}=4; b=min{9;6;8}=6.
Так как a¹b, то седловая точка отсутствует и оптимальное решение следует искать в смешанных стратегиях игроков: S*A= (р1,р2,р3) и S*B= (q1, q2,q3). Обозначив 
составим две взаимно-двойственные ЗЛП:
1) для определения оптимальной стратегии игрока A имеем следующую задачу линейного программирования: найти min Z = x1 + x2 + x3 при ограничениях
xi ³ 0, i=1,2,3.
2) двойственная задача для определения оптимальной стратегии игрока B формулируется так: найти max L= y1 + y2 + y3 при ограничениях
yj ³ 0, j=1,2,3.
Решаем симплексным методом одну из задач, например 2, т.к. для нее 1-е базисное решение будет допустимым. В результате получаем следующее решение: Y=(1/2; 0; 17/27; 2/27; 0; 1/9), max L=5/27.
Установим соответствие между переменными взаимно-двойственных ЗЛП и определим оптимальное базисное решение задачи 1 с помощью теорем двойственности: 
Оптимальное базисное решение задачи 1: X=(2/27; 0; 1/9; ½; 0; 17/27), причем minZ=maxL=5/27. Находим цену игры =27/5=5,4. Оптимальную стратегию S*A= (р1,р2,р3) находим, используя рi*= vxi (I=1,2,3), т.е. S*A= (0,4; 0; 0,6).
Следовательно, предприятие должно выпустить 40% продукции А1 и 60% продукции А3, а продукцию А2 не выпускать.
Оптимальную стратегию S*B= (q1, q2,q3) находим аналогично: qj*= vyj (j=1,2,3), т.е. S*B= (0,2; 0; 0,8; 0) (здесь учтено, что2-ой столбец исходной матрицы был отброшен как невыгодный). Т.о. оптимальный спрос в 20% находится в состоянии В1 и в 80% - в состоянии В3.
Контрольные вопросы
1. Предмет теории игр на основе понятия матричных игр.
2. Решение игр с седловой точкой. Принцип минимакса.
3. Решение игр размером 2х2 в смешанных стратегиях.
4. Геометрическая интерпретация игры 2х2.
5. Графический метод решения игры 2xn.
