С помощью рассмотренных методов построения первоначального плана можно получить вырожденный или невырожденный опорный план. Построенный опорный план ТЗ как ЗЛП можно было бы довести до оптимального с помощью симплекс-метода. Однако из-за громоздкости симплексных таблиц, содержащих mn переменных, и большого объема вычислительных работ для получения оптимального плана используют более простые методы, самый распространенный из которых метод потенциалов (модифицированный распределительный метод).
Пусть имеется ТЗ с балансовыми условиями
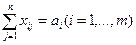 ;
; 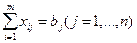 , причем
, причем  .
.
Стоимость перевозки единицы груза из Ai в Bj равна cij; таблица стоимостей (cij) задана. Требуется найти план перевозок (xij), который удовлетворял бы балансовым условиям, и при этом стоимость всех перевозок была минимальна:
L =  ® min.
® min.
Идея метода потенциалов. Представим себе, что каждый из пунктов отправления Ai вносит за перевозку груза сумму Ui, в свою очередь каждый из пунктов назначения Bj также вносит за перевозку единицы груза сумму Vj.
Обозначим Ui + Vj =  (i=1,...,m; j=1,...,n) и будем называть
(i=1,...,m; j=1,...,n) и будем называть  «псевдостоимостью» перевозки единицы груза из Ai в Bj. Ui, и Vj не обязательно должны быть положительными. Обозначим совокупность платежей U1,..., Um, V1,..., Vn через (Ui, Vj).
«псевдостоимостью» перевозки единицы груза из Ai в Bj. Ui, и Vj не обязательно должны быть положительными. Обозначим совокупность платежей U1,..., Um, V1,..., Vn через (Ui, Vj).
Предположим, что план (xij) невырожденный, т.е. число базисных клеток в таблице перевозок равно m + n - 1. Для всех этих клеток xij > 0. Определим платежи
(Ui, Vj) так, чтобы во всех базисных клетках псевдостоимости были равны стоимостям:
 =Ui + Vj = cij при xij > 0;
=Ui + Vj = cij при xij > 0;
Что касается свободных клеток, то для них соотношение между псевдостоимостями и стоимостями может быть каким угодно:
 = cij или
= cij или  > cij или
> cij или  < cij.
< cij.
Теорема. Если план  ТЗ является оптимальным, то можно отыскать систему из m+n чисел
ТЗ является оптимальным, то можно отыскать систему из m+n чисел  и
и  , для которой будут выполняться равенства:
, для которой будут выполняться равенства:
(1)  +
+  =cij для
=cij для  >0, где сij – элементы матрицы транспортных затрат, соответствующие занятым данным решением клеткам;
>0, где сij – элементы матрицы транспортных затрат, соответствующие занятым данным решением клеткам;
(2)  +
+  £cij для
£cij для  =0, где сij – элементы матрицы, соответствующие незанятым оптимальным решением клеткам.
=0, где сij – элементы матрицы, соответствующие незанятым оптимальным решением клеткам.
Числа  и
и  называются потенциалами соответственно поставщиков и потребителей.
называются потенциалами соответственно поставщиков и потребителей.
Доказательство.
ТЗ минимизации линейной функции L =  при ограничениях
при ограничениях

можно рассматривать как двойственную некоторой исходной ЗЛП, условия которой получают по общей схеме, рассмотренной выше, если каждому ограничению вида (*) в исходной задаче соответствует переменная Ui (i=1,2,…,m), а каждому ограничению вида (**) – переменная Vj (j=1,2,…,n), а именно максимизировать линейную функцию Z=  при ограничениях
при ограничениях 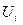 +
+  £cij (i=1,2,…,m, j=1,2,…,n). План Х* - оптимальный план двойственной задачи, поэтому план Y*=(
£cij (i=1,2,…,m, j=1,2,…,n). План Х* - оптимальный план двойственной задачи, поэтому план Y*=( ,
,  ) является планом исходной задачи и на основании второй теоремы двойственности Lmax=Zmin
) является планом исходной задачи и на основании второй теоремы двойственности Lmax=Zmin
или
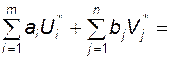

На основании второй теоремы получаем, что ограничения исходной задачи, соответствующие положительным компонентам оптимального плана двойственной задачи, удовлетворяются удовлетворяются как строгие равенства, а соответствующие компонентам, равным нулю, - как неравенства, т.е.
 +
+  =cij для x* ij>0;
=cij для x* ij>0;
 +
+  £cij для x* ij=0.
£cij для x* ij=0.
¨
План, обладающий таким свойством, называется потенциальным. Всякий потенциальный план является оптимальным.
На основании теоремы для того, чтобы первоначальный план был оптимальным, необходимо выполнение следующих условий:
а) для каждой занятой клетки сумма потенциалов должна быть равна стоимости единицы перевозки, стоящей в этой клетке:
(1)  +
+  =cij при xij>0;
=cij при xij>0;
б) для каждой незанятой клетки сумма потенциалов должна быть меньше или равна стоимости единицы перевозки, стоящей в этой клетке:
(2)  +
+  £cij при xij=0.
£cij при xij=0.
Если хотя бы одна незанятая клетка не удовлетворяет условию(2), то опорный план является неоптимальным и его можно улучшить, вводя в базис вектор, соответствующий клетке, для которой нарушается условие оптимальности (т.е. в клетку надо переместить некоторое количество груза). Таким образом, для проверки плана на оптимальность необходимо сначала построить систему потенциалов.
Рассмотрим алгоритм решения ТЗ методом потенциалов и проиллюстрируем его применение на примере:
Пример. Решить ТЗ, исходные данные которой заданы в таблице 1.
Табл. 1
| ПН ПО | B1 | B2 | B3 | B4 | Запасы ai |
| A1 | |||||
| A2 | |||||
| A3 | |||||
| Заявки bj | 1000¹1100 |
1. Проверка выполнения необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводится фиктивный поставщик или потребитель с недостающими запасами или запросами и нулевыми стоимостями перевозок.
Находим суммарные запасы поставщиков и суммарные запасы потребителей:

Задача с неправильным балансом. Вводим 4-го, фиктивного поставщика с запасами а4=1100-1000=100 и нулевыми стоимостями перевозок единиц груза (см. табл. 2).
2. Построение первоначального опорного плана (методом минимальной стоимости или другим методом), проверка правильности его построения по количеству занятых клеток (их должно быть m+n-1). Убедиться в линейной зависимости векторов условий (используя метод вычеркивания).
Находим первоначальный опорный план методом минимальной стоимости (см. табл. 2). Полученное решение Х1 имеет 4+4-1=7 базисных переменных.
Табл. 2
| ПН ПО | B1 | B2 | B3 | B4 | Запасы ai |
| A1 | - | - | - | ||
| A2 | - | - | |||
| A3 | - | ||||
| Aф | - | - | - | ||
| Заявки bj | 1100=1100 |
Вычисляем значение целевой функции на этом опорном плане:
Z(X)=1*200+2*200+3*100+7*100+9*300+12*100+0*100=5300.
3. Построение системы потенциалов. Группа равенств (1) используется как система уравнений для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных Ui, I=1,2,…,m и Vj, j=1,2,…,n. Число уравнений системы и число отличных от нуля компонент невырожденного опорного плана равно m+n-1, т.е. m+n-1 занятых клеток. Уравнений на одно меньше, чем неизвестных, поэтому система является неопределенной и одному неизвестному (обычно U1) придают нулевое значение. После этого остальные потенциалы определяются однозначно из системы.
В случае вырожденного опорного плана, т.е. когда занятых клеток меньше m+n-1, то остаются неопределенные потенциалы. Для устранения вырожденности дополняют количество занятых клеток до m+n-1, вводя нулевые перевозки. Клетки, в которые введены нулевые перевозки, называются фиктивно занятыми. Причем, т.к. задача решается на минимизацию линейной функции, целесообразно сделать фиктивно занятой ту клетку, в которой стоит наименьшая стоимость.
Значения потенциалов записываем рядом с запасами или запросами соответствующих поставщиков и потребителей. Система уравнений для нахождения потенциалов достаточно проста, обычно ее решают устно. Любой неизвестный потенциал, соответствующий занятой клетке, равен находящейся в этой клетке стоимости минус известный потенциал, соответствующий этой же клетке.
Проверяем правильность построения системы. Для этого просматриваем занятые клетки строк и для каждой из них определяем сумму потенциалов. Если для всех занятых клеток выполняется (1), то система построена правильно, в противном слу-чае ее надо построить заново или изменить так, чтобы условие (1) выполнялось.
В нашем примере записываем систему уравнений для нахождения потенциалов и решаем ее:
U1+V4=1,
U2+V1=2,
U2+V2=3,
U3+V2=7,
U3+V3=9,
U3+V4=12,
U4+V4=0.
Пусть U3=0, тогда V2=7- U3=7,
V3=9- U3=9, V4=12- U3=12,
U1=1-V4=-11, U4=0-V4=-12,
U2=3-V2=-4, V1=2- U2=6.
Табл. 3
| V1=6 | V2=7 | V3=9 | V4=12 | |
| U1=-11 | ||||
| U2=-4 |    - 3 - 3
|  5 5
|  + 6 + 6
  2 2
| |
 U3=0 U3=0
|
 0 0
| + 7
 100 100
| - 12 | |
| U4=-12 |
4. Проверка выполнения условия оптимальности для свободных клеток с помощью группы неравенств (2)  +
+  £cij при xij=0. Для чего просматриваем строки и для каждой незанятой клетки проверяем выполнение условия (2), т.е. суммируем потенциалы, на пересечениях которых стоит незанятая клетка, сумму сравниваем со стоимостью, стоящей в ней.
£cij при xij=0. Для чего просматриваем строки и для каждой незанятой клетки проверяем выполнение условия (2), т.е. суммируем потенциалы, на пересечениях которых стоит незанятая клетка, сумму сравниваем со стоимостью, стоящей в ней.
Условие оптимальности: если для всех незанятых клеток Ui+Vj£cij, то план оптимальный, если для некоторых клеток Ui+Vj>cij, то план неоптимальный, необходимо перейти к новому опорному плану, на котором значение целевой функции будет меньше.
Для каждой свободной клетки, в которой не выполняется условие оптимальности, находим величину разности Dij=(Ui+Vj)-Сij>0 и записываем ее значение в левый нижний угол этой же клетки. Числа Dij называются оценками для свободных клеток таблицы (векторов условий) ТЗ.
Тогда условие оптимальности можно перефразировать: опорный план является оптимальным, если для всех клеток таблицы (векторов условий) оценки неположительные Dij£0.
Для нашего примера найдены положительные оценки D23=0, D24=2, D31=0. Начальной опорное решение не является оптимальным, т.к. имеется положительная оценка D24=2. См. табл. 3.
5. Выбор клетки, в которую необходимо послать перевозку.
ТЗ решается на минимум линейной функции, поэтому алгоритм ее решения также следует общим принципам алгоритма симплекс-метода решения задач на минимум.
Если отождествлять занятые клетки с векторами, составляющими базис, а свободные – с остальными векторами системы ограничений, то в ОЗЛП в базис включается тот вектор, которому соответствует максимальная оценка целевой функции. В ТЗ загрузке подлежит в первую очередь клетка, например (l,k), которой соответствует наибольшая положительная оценка D lk =  {Dij}=
{Dij}=  [(Ui+Vj)-Сij].
[(Ui+Vj)-Сij].
Выбираем клетку, в которую пошлем перевозку  {D24=2}=D24.
{D24=2}=D24.
6. Построение цикла и определение величины перераспределения груза.
Для определения количества единиц груза, подлежащих перераспределению, отмечаем знаком «+» свободную клетку, которую надо загрузить. Это означает, что клетка присоединяется к занятым клеткам. В таблице занятых клеток стало m+n, поэтому появляется цикл, все вершины которого, за исключением клетки, отмеченной знаком «+», находятся в занятых клеток, причем этот цикл единственный. Стрелками будем показывать направление обхода цикла. Отыскиваем цикл и, начиная движение от клетки, помеченной знаком «+», поочередно проставляем знаки «-» и «+».
Затем находим q0= 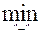 {xij}, где xij – перевозки, стоящие в вершинах цикла, отмеченных знаком «-». Величина q0 определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение q0 записываем в свободную клетку со знаком «+». Двигаясь по циклу, вычитаем q0 из объемов перевозок в клетках со знаком «-», и прибавляем к объемам перевозок в клетках со знаком «+». Если q0 соответствуют несколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном опорном плане занятых клеток было m+n-1.
{xij}, где xij – перевозки, стоящие в вершинах цикла, отмеченных знаком «-». Величина q0 определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение q0 записываем в свободную клетку со знаком «+». Двигаясь по циклу, вычитаем q0 из объемов перевозок в клетках со знаком «-», и прибавляем к объемам перевозок в клетках со знаком «+». Если q0 соответствуют несколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном опорном плане занятых клеток было m+n-1.
Отмечаем «+» клетку (2,4) и для нее строим цикл, присоединяя ее к занятым клеткам. Применяя метод вычеркивания, находим цикл (2,4), (3,4), (3,2), (2,2).
Начиная с клетки (2,4) с «+», поочередно в вершинах расставляем знаки. Определим величину q0 , перераспределяемую по циклу, она равна значению наименьшей из перевозок в клетках со знаком «-»:q0=100.
6. В результате перераспределения q0 получен новый опорный невырожденный план, который снова подлежит проверке на оптимальность. Для проверки на оптимальность нового плана вновь строим систему потенциалов и проверяем выполнение условия оптимальности для каждой незанятой клетки.
Если полученный план снова окажется неоптимальным, то следует выполнить вычисления, приведенные в п. 5. Процесс повторяется до тех пор, пока все незанятые клетки не будут удовлетворять условию  +
+  £cij.
£cij.
В нашем примере полученный план оказался неоптимальным, следует выполнить вычисления, приведенные в п. 5.
Приложения транспортной задачи к решению некоторых экономических задач
ТЗ применяется при решении экономических задач, которые по своему характеру не имеют ничего общего с транспортировкой груза, поэтому величины Сij могут иметь различный смысл.
1. Увеличение производительности автомобильного транспорта за счет минимизации порожнего пробега.
2. Оптимальное закрепление за станками операций по обработке деталей.
3. Оптимальные назначения или проблема выбора.
4.Задачи размещения с учетом транспортных и производственных затрат.
Контрольные вопросы
1. Транспортная задача: постановка и ее математическая модель.
2. Открытые и закрытые модели транспортных задач.
3. Необходимое и достаточное условие разрешимости транспортных задач.
4. Построение первоначального опорного плана транспортных задач методом северо-западного угла.
5. Построение первоначального опорного плана транспортных задач методом минимальной стоимости.
6. Решение транспортных задач методом потенциалов. Критерий оптимальности решения транспортных задач.
Понятие цикла.
Рекомендованная литература: [ 3, 5, 6, 7, 8, 11]






