Пусть даны две взаимно-двойственные симметричные задачи.
Исходная: найти максимальное значение линейной функции
L=CХ®max (1)
при ограничениях: АХ£В (2)
Х ³ 0 (3)
Двойственная: найти минимальное значение линейной функции
Z=BY→min (4)
при ограничениях: АY³В (5)
Y ³ 0 (6)
Если каждую из задач решать симплексным методом, то необходимо привести их к каноническому виду. Для чего в систему ограничений (2) (в краткой записи 
) следует ввести m неотрицательных переменных xn+1,…,xn+i,…,xn+m, а в систему ограничений (5) (
) - n неотрицательных переменных ym+1,…,ym+j,…, yn+m, где i(j) – номер неравенства, в которое введена дополнительная переменная.
Системы ограничений каждой из взаимно-двойственных задач примут вид:
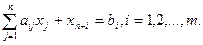(7)
(8)
Как в cистеме (7), так и в системе (8) m+n неизвестных. Выберем в качестве базисных переменных в (7) переменные xn+1,…,xn+i,…,xn+m, в (8) – переменные ym+1,…,ym+j,…, yn+m.
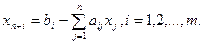(9)
(10)
Установим соответствие между переменными одной из двойственных задач и переменными другой задачи. Рассмотрим переменную xn+1 из (9), выраженную через коэффициенты a11, a12,…,a1n:
.
Именно с этими же коэффициентами входит в уравнения системы (10) переменная y1:
Вот и поставим в соответствие переменной xn+1 переменную y1. Рассуждая аналогично получим следующую таблицу.
| Переменные исходной задачи I | |
| Первоначальные | Дополнительные |
| x1 x2 … xj …. xn ↕ ↕ ↕ ↕ ym+1 ym+2 … ym+j …. ym+n | xn+1 xn+2 … xn+i …. xn+m ↕ ↕ ↕ ↕ (11) y1 y2 … yj …. ym |
| Дополнительные | Первоначальные |
| Переменные двойственной задачи II |
Очевидно, что коэффициенты, с которыми свободные переменные входят в выражение для базисной переменной xn+j (j=1,2,…,m) в системе (9), отличаются лишь знаком от коэффициентов, с которыми свободная переменная yj (она соответствует xn+j) входит в уравнения системы (10).
Теорема. Положительным (ненулевым) компонентам оптимального решения одной из взаимно-двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых i=1,2,…,m и j=1,2,…,n выполняется:
если x*j>0, то y*m+j=0; если x*n+i>0, то y*j=0, и аналогично, если y*j>0, то x*n+i=0; если y*m+j>0, то x*j=0.
Доказательство. Выразим дополнительные переменные из систем ограничений (7) исходной задачи I и двойственной задачи II, представленных в каноническом виде
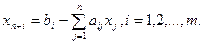(12)
(13)
Умножим каждое равенство системы (12) на соответствующие переменные yj ³ 0 и сложим полученные равенства:
(14)
Аналогично, умножая каждое равенство системы (13) на соответствующие переменные xj ³ 0 и сложив полученные равенства, найдем:
(15)
Равенства (14) и (15) будут справедливы для любых допустимых значений переменных, в том числе и для оптимальных значений x*j, x*n+i, y*i, y*m+j.
В силу первой теоремы двойственности L(Х*)= Z(Y*) или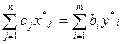 
, поэтому из записи правых частей (14) и (15) следует, что эти правые части должны отличаться только знаком.
С другой стороны, из неотрицательности левых частей выражений (14) и (15)
и 
следует, что те же правые части этих равенств должны быть неотрицательны.
Эти два условия могут выполняться одновременно только при равенстве правых частей для оптимальных значений переменных нулю, следовательно и левые части равны нулю:
В силу неотрицательности переменных каждое слагаемое в этих равенствах должно равняться нулю:
Отсюда вытекает заключение теоремы, что если x*n+i>0, то y*j=0, и аналогично, если y*j>0, то x*n+i=0 (из первого равенства); если x*j>0, то y*m+j=0 и аналогично, если y*m+j>0, то x*j=0.¨
Из рассмотренной теоремы следует важный вывод: соответствие (11) между переменными взаимно-двойственных задач при достижении оптимума, т.е. на последнем шаге решения каждой задачи симплексным методом, представляет соответствие между базисными как правило, не равными нулю, переменными одной из двойственных задач и свободными, равными нулю, переменными другой задачи, когда они образуют допустимые базисные решения.
