Вторая теорема двойственности.

Рекомендованная литература: [ 3, 5, 6, 7, 8, 11]

Тема 7. Транспортная задача линейного программирования

 

Розглянуті питання з теми:

Постановка задачи

Нахождение опорного плана

Метод последовательного улучшения плана перевозок, цикл пересчета

Решение транспортной задачи методом потенциалов

 

Постановка задачи

 

Транспортная задача линейного программирования широко применяется как в теоретических разработках, так и в практике планирования различных экономических процессов. Особо важное значение она имеет при решении вопросов рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта.

Рассмотрим постановку задачи и ее математическую модель.

Пусть некоторый однородный продукт, сосредоточенный у m поставщиков A₁,A₂,...,A_m в количестве соответственно a₁, a₂,..., a_m единиц, необходимо доставить n потребителям B₁, B₂,..., B_n в количестве b₁, b₂,..., b_n единиц. Известна стоимость c_ij перевозки единицы груза от i-го поставщика к j-ому потребителю, заданная в виде таблицы (матрицы): .

Требуется составить такой план перевозок, при котором все заявки были бы выполнены, и при этом общая стоимость всех перевозок была бы минимальна.

Т.к. здесь показатель эффективности - стоимость, то поставленную задачу называют транспортной задачей по критерию стоимости.

Математическая модель транспортной задачи: обозначим через x_ij - количество единиц груза, направляемого из i-го пункта отправления A_i в j-й пункт назначения B_j (i=1,..., m; j=1,...,n), и которые будем называть перевозками. Все переменные x_ij ³ 0, их количество - m×n. Эти переменные могут быть записаны в виде матрицы перевозок Х= .

Так как от i-го поставщика к j-ому потребителю запланировано к перевозке x_ij единиц груза, то стоимость одной перевозки составит с_ijx_ij. Стоимость всего плана выразится двойной суммой, т.к. суммирование производится по всем комбинациям индексов (i=1,...,m; j=1,...,n), т.е. по всем комбинациям пунктов отправления с пунктами назначения. Причем суммарная стоимость всех перевозок, т.е. сумма всех x_ij, умноженных на соответствующие стоимости c_ij, должна быть минимальной:

L= =min, (1)

Систему ограничений получаем из следующих условий:

1. Суммарное количество груза, направляемое из каждого пункта отправления во все пункты назначения, должно быть равно запасу груза в данном пункте, т.е. все грузы должны быть вывезены. Это даст нам m условий-равенств:

(2)

2. Суммарное количество груза, доставляемое в каждый пункт назначения изо всех пунктов отправления, должно быть равно заявке, поданной данным пунктом, т.е. все потребности должны быть удовлетворены. Это даст нам n условий-равенств:

(3)

Мы имеем типичную ЗЛП с ограничениями-равенствами. Математическая формулировка ТЗ будет следующей: на множестве неотрицательных (допустимых) решений системы ограничений найти такое решение X=(x₁₁,x₁₂,…,x_ij, …,x_mn), при котором значение линейной функции (1) минимально.

В рассмотренной модели предполагается, что сумма всех заявок равна сумме всех запасов (4)

Если суммарная мощность поставщиков равна суммарной мощности потребителей, т.е. , такая задача называется задачей с правильным балансом, а ее модель закрытой. В противном случае ТЗ называется задачей с неправильным балансом, а ее модель открытой.

Для открытой модели возможны два случая:

а) суммарные запасы превышают суммарные потребности ;

б) суммарные потребности превышают суммарные запасы .

Линейная функция одинакова в обоих случаях.

Открытая модель решается приведением к закрытой модели.

В случае (а), когда суммарные запасы превышают суммарные потребности, сверх имеющихся n пунктов назначения B₁, B₂,..., B_n вводится фиктивный потребитель В_n+1 (B_ф), потребности которого 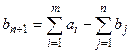. Положим стоимости всех перевозок из всех ПО в фиктивный ПН B_ф равными нулю: c_iф = 0 (i=1,...,m)., т.к. груз не перевозится. Т.о., отправление какого-то количества груза x_iф из пункта A_i в пункт B_ф попросту будет означать, что в пункте A_i осталось не отправленным x_iф ед. груза. Введением b_ф сравнивается баланс ТЗ.

В случае (б), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик А_m+1 (A_ф), запасы которого . Положим стоимость перевозок из ПО A_ф в любой ПН равным нулю: c_фj=0(j=1,...,n). Т.е. какая-то часть заявок x_фj на каждом пункте останется неудовлетворенной, будем считать, что она как бы покрывается за счет фиктивного ПО A_ф.

Таким образом, стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, т.к. груз в обоих случаях не перевозится.

После преобразований задача принимает вид закрытой модели и решается обычным способом. При равных стоимостях перевозки единицы груза от поставщиков к фиктивному потребителю затраты на перевозку груза реальным потребителям минимальны, а фиктивному потребителю будет направлен груз от наименее выгодных поставщиков. То же самое получаем и в отношении фиктивного поставщика.

Условие задачи в определенном порядке можно записать в виде таблицы, которую назовем транспортной таблицей или матрицей планирования.

ПН ПО	B1	B2	...	Bn	Запасы ai
A1	c11 x11	c12 x12	...	c1n x1n	a1
A2	c21 x21	c22 x22	...	c2n x2n	a2
...	...	...	...	...	...
Am	cm1 xm1	cm2 xm2	...	cmn xmn	am
Заявки bj	b1	b2	...	bn

В транспортной таблице записываются

n пункты отправления и запасы, имеющиеся в пунктах отправления,

n пункты назначения и заявки, поданные пунктами назначения,

n стоимости перевозок из каждого пункта отправления в каждый пункт назначения в правом верхнем углу каждой ячейки

n количество единиц груза x_ij, запланированных к перевозке от i-го поставщика к j-му потребителю в самой ячейке.

Клеткой (i,j) называется клетка, стоящая в i-й строке и j-м столбце транспортной таблицы.

Пример. Составить математическую модель ТЗ, исходные данные которой таковы:

ПН ПО	B1	B2	Bn	Запасы ai
A1
A2
Заявки bj

Введем переменные задачи (матрицу перевозок) Х=

Запишем матрицу стоимостей С= .

Целевая функция равна сумме произведений всех соответствующих элементов матриц С и Х: Z(X)= 9x₁₁+5x₁₂+3x₁₃+4x₂₁+6x₂₂+8x₂₃. Она должна достигать минимального значения.

Составим систему ограничений задачи. Сумма всех перевозок, стоящих в 1-ой строке матрицы Х, должна равняться запасам 1-го поставщика, сумма перевозок во 2-ой строке матрицы Х - запасам 2-го поставщика:

x₁₁+x₁₂+x₁₃=90,

x₂₁+x₂₂+x₂₃=110. Это значит, что запасы поставщиков вывозятся полностью.

Суммы перевозок, стоящих в каждом столбце матрицы Х, должны быть равны запасам соответствующих потребителей:

x₁₁+x₂₁=50,

x₁₂+x₂₂=70,

x₁₃+x₂₃=80. Это значит, что запросы потребителей удовлетворяются полностью.

Перевозки не могут быть отрицательными: x_ij>=0, i=1,2,..,m; j=1,2,...,n.

Математическую модель: найти переменные задачи, обеспечивающие минимум функции Z(X)= 9x₁₁+5x₁₂+3x₁₃+4x₂₁+6x₂₂+8x₂₃ и удовлетворяющие системе ограничений

x₁₁+x₁₂+x₁₃=90,

x₂₁+x₂₂+x₂₃=110,

x₁₁+x₂₁=50,

x₁₂+x₂₂=70,

x₁₃+x₂₃=80,

и условиям неотрицательности x_ij>=0, i=1,2,..,m; j=1,2,...,n.

 

Рассмотрим необходимое и достаточное условие разрешимости задачи.

Теорема. Любая транспортная задача, у которой суммарный объем запасов совпадает с суммарным объемом потребностей, т.е.

,

имеет решение.

Доказательство. Необходимо показать, что при заданных условиях существует хотя бы один план задачи и линейная функция на множестве планов ограничена.

Пусть =М>0. Тогда величины x_ij=a_ib_j/M (i=1,2,…,m; j=1,2,…,n) являются планом, т.к. они удовлетворяют системе ограничений (2) и (3). Действительно, подставляя значения x_ij в (2) и (3), имеем

Выберем из значений С_ij наибольшее С’=max C_ij и заменим в линейной функции L= все коэффициенты на С'; тогда, учитывая (2), получаем £C’ =C’ 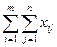=C’M.

Выберем из значений С_ij наименьшее С’’=minC_ij и заменим в линейной функции L= все коэффициенты на С'’; тогда, учитывая (2), получаем ³C’’ =C’’ =C’’M.

Объединяя два последних неравенства в одно двойное, окончательно получим

C’’M£L£C’M,

т.е. линейная функция ограничена на множестве планов ТЗ.¨

 

 

Нахождение опорного плана

 

Решение ТЗ, как и других ЗЛП, начинается с нахождения опорного плана. В отличие от ОЗЛП с произвольными ограничениями и минимизируемой функцией, решение ТЗ всегда существует.

Любая совокупность значений (x_ij) (i=1,...,m; j=1,...,n), удовлетворяющая условиям (2), (3) (так называемым «балансовым условиям»): все заявки удовлетворены, все запасы исчерпаны называется допустимым планом перевозок (решением).

Если полученное решение позволяет минимизировать расходы на транспортировку, т.е. если план (x_ij) среди всех допустимых планов приводит к наименьшей стоимости всех перевозок, то решение называется оптимальным или оптимальным планом.

Опр.1. Опорным планом ТЗ называется любой допустимый план, для которого векторы условий, соответствующие положительным компонентам, линейно независимы, т.е. если в допустимом плане отличны от нуля не более r=m+n-1 базисных перевозок x_ij, а остальные перевозки равны нулю.

Система ограничений закрытой ТЗ содержит m+n уравнений, связанных соотношением , и mn переменных. Не все m+n уравнений нашей задачи являются линейно независимыми. Так, складывая между собой почленно все уравнения (2) 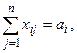i=1,2,…,m и все уравнения (3) j=1,2,…,n, получаем два одинаковых уравнения. В транспортной таблице такое сложение равнозначно соответственно по членному сложению столбцов и почленному сложению строк.

Наличие в системе ограничений 2-х одинаковых уравнений говорит о ее линейной зависимости. Если одно из этих уравнений отбросить, то в общем случае система ограничений должна содержать m+n-1 линейно независимых уравнений.

Опорный план называется невырожденным, если он содержит m+n-1 положительных компонент (перевозок), иначе он называется вырожденным.

Таким образом, если каким-либо способом получен невырожденный опорный план ТЗ, то в матрице (i=1,2,…,m; j=1,2,…,n) значений его компонент положительными являются только m+n-1, а остальные равны нулю.

Опр.2. Опорным планом ТЗ называется любой допустимый план в котором отличны от нуля не более m+n-1 перевозок, а остальные равны нулю.

Клетки таблицы, в которых мы будем записывать отличные от нуля перевозки, условимся называть занятыми, а остальные (пустые) - свободными. Занятые клетки соответствуют базисным переменным, и для невырожденного опорного плана их количество равно m+n-1.

Как известно, базисным переменным, включенным в опорный план, соответствует система линейно независимых векторов.

Для проверки линейной независимости векторов условий, соответствующих компонентам допустимого плана, используют циклы.

Циклом называется такая последовательность клеток таблицы ТЗ (i₁,j₁),(i₁,j₂),(i₂,j₂),...,(i_k,j₁), в котором только две соседние клетки расположены в одном столбце или одной строке таблицы, причем последняя клетка находится в той же строке или столбце, что и первая. Построение циклов начинают какой-либо занятой клетки, вычерчивают вспомогательную линию, параллельную столбцам или строкам таблицы к другой занятой клетке, в которой возможен поворот под углом 90°, и продолжают вычерчивание к следующей занятой клетке, стремясь возвратиться к исходной клетке. Если такой возврат возможен, то получен цикл и план является не опорным. Клетки, в которых происходит поворот под прямым углом, определяют вершины цикла.

Система векторов условий ТЗ линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимый план ТЗ Х= (i=1,2,…,m; j=1,2,…,n) является опорным только в том случае, когда из занятых им клеток нельзя образовать ни одного цикла, все вершины которого лежат в занятых клетках.

Если к занятым клеткам, определяющим опорный невырожденный план, присоединить какую-то незанятую клетку, то план станет не опорным, т.к. занятых клеток станет m+n-1, появится единственный цикл, все вершины которого, за исключением одной, лежат в занятых клетках.

Для проверки возможности образования цикла используется метод вычеркивания:

1. Если в строке или столбце таблицы одна занятая клетка, то она не может входить в какой-либо цикл, т.к. имеет только две клетки в каждой строке или столбце. Следовательно, можно вычеркнуть все строки таблицы, содержащие по одной занятой клетке, затем вычеркнуть все столбцы, содержащие по одной занятой клетке, далее вернуться к строкам и продолжить вычеркивание строк и столбцов.

2. Если в результате вычеркиваний все строки и столбцы будут вычеркнуты, значит из занятых клеток таблицы нельзя выделить часть, образующую цикл, и система соответствующих векторов условий линейно независима, а решение – опорное. Если же после вычеркиваний остается часть клеток, то они образуют цикл, система соответствующих векторов условий линейно зависима, а решение – не опорное.

 

Существует несколько схем построения первоначального опорного плана:

1. Простейший метод - метод северо-западного угла. Согласно данному методу запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.

Заполнение таблицы ТЗ начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или потребитель.

Существенный недостаток метода ”северо-западного” угла состоит в том, что он построен без учета значений стоимости перевозки единицы груза.