Теорема. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.
Пример 1. Даны две взаимно двойственные задачи:
L=2x1+3x2®max
при ограничениях 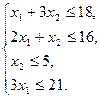 x1³0, x2³ x1³0, x2³
| Z=18y1+16y2+5y3+21y4®min при ограничениях:
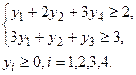
|
Эти задачи решены ранее и получены оптимумы линейных функций Lmax=24, Zmin=24. Убедимся в справедливости второй теоремы двойственности.
Установим следующее соответствие между переменными:
| x1 x2 x3 x4 x5 x6 ↕ ↕ ↕ ↕ ↕ ↕ y5 y6 y1 y2 y3 y4 |
Обе задачи были решены симплексным и на последнем шаге решения каждой задачи получено 7
| L=24-4/5x3-3/5x4-0x5-0x6-0x1-0x2 L(X*)=Lmax=24 при оптимальном базисном решении X*=(6;4;0;0;1;3) | Z=24+6y5+4y6+0y1+0y2+ y3+3y4 Z(Y*)=Zmin=24 при оптимальном базисном решении Y*=(4/5;3/5;0;0;0;0) |
Компоненты оптимального решения двойственной задачи (4/5;3/5;0;0;0;0) равны по абсолютной величине коэффициентам при соответствующих переменных целевой функции L, а компоненты оптимального решения исходной задачи (6;4;0;0;1;3) равны коэффициентам при соответствующих переменных целевой функции Z.
Вторая теорема двойственности. Для того чтобы допустимые решения Х*=(x*1, x*2 , …x*j, …, x*n), Y*=(y*1, y*2 , …, y*i, …, y*m) являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства:
a) 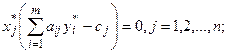
b) 
Иначе, a) если при подстановке оптимального решения в систему ограничений j-е ограничение двойственной задачи выполняется как строгое неравенство, т.е., 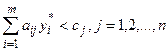 , то j-я компонента оптимального решения исходной задачи
, то j-я компонента оптимального решения исходной задачи 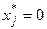 , и, наоборот, если j-я координата оптимального решения задачи
, и, наоборот, если j-я координата оптимального решения задачи 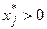 , то j-е ограничение двойственной задачи
, то j-е ограничение двойственной задачи 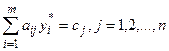 ;
;
б) если при подстановке оптимального решения в систему ограничений i-е ограничение исходной задачи 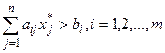 , то i-я компонента оптимального решения двойственной задачи
, то i-я компонента оптимального решения двойственной задачи 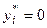 , и, наоборот, если i-я координата оптимального решения двойственной задачи
, и, наоборот, если i-я координата оптимального решения двойственной задачи 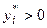 , то i-е ограничение исходной задачи
, то i-е ограничение исходной задачи 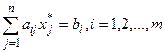
(без доказательства).
Пример. Для задачи составить двойственную, получить решение, например графически и, используя 2-ю теорему двойственности, найти решение исходной задачи:
L(X)=-2x1+4x2+14x3+2x4®min,
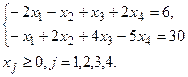
Решение. Составим двойственную задачу: Z(Y)+6y1+30y2®max,
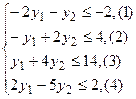
Пусть получили оптимальное решение Y*=(2;3), значение Z(Y*)=102. Подставим оптимальное решение Y*=(2;3) в систему ограничений. Получим, что ограничения (1) и (4) выполняются как строгие неравенства: 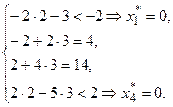
Согласно 2-й теореме двойственности соответствующие координаты исходной задачи, равны 0: x*1=x*4=0. Учитывая это, из системы ограничений исходной задачи получим 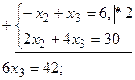
Отсюда х*3=7, х*2=1. Х*=(0,1,7,0); minL(X)=102.






