Система единичных векторов n-мерного векторного пространства

Введем понятие системы единичных векторов n-мерного векторного пространства. Если положить, что j-я компонента вектора E_j равна единице, а остальные равны нулю, то при j =1, 2,..., n получим систему

(*)

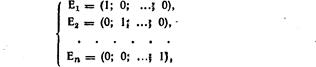которая называется системой единичных векторов n-мерного векторного пространства.

Система единичных векторов (*) образует одинизбазисов n-мерного векторного пространства; компоненты же любого n-мерного вектора можно считать координатами этого вектора в единичном базисе.

Докажем это утверждение. Покажем, что система единичных векторов линейно независима. Составим соотношение

k₁E₁+k₂E₂+...+k_nE_n =0.

Подставляя вместо E₁, E₂,...,E_n их выражения, умноженные соответственно на k_j, и складывая, получим

(k₁,k₂,…,k_n) = (0; 0;...; 0),

откуда k₁=0, k₂=0,…,k_n =0. Таким образом, система векторов (*) линейно независима.

С другой стороны, всякий n-мерный вектор А = (a₁, a₂,...,a_n) представляет собой линейную комбинацию векторов этой системы:

A= a₁E₁+a₂E₂+...+a_nE_n = (a₁, a₂,...,a_n)

Пример, вектор А = (3;-2; 4; -5) можно записать как линейную комбинацию единичных векторов E₁= (1; 0; 0; 0); E₂ = (0; 1;0;0); Ез = (0; 0; 1; 0); Е₄ =(0; 0; 0; 1) с коэффициентами, которые равны компонентам вектора А:

А = ЗЕ₁ - 2Е₂ + 4Ез - 5Е₄ = (3; - 2; 4; - 5).

Вычислим ранг матрицы, используя теоремы 1.3. Назовем элементарными следующие преобразования матрицы:

- перемену мест двух строк или столбцов;

- умножение строки или столбца на произвольное, отличное от нуля число;

- прибавление (вычитание) к одной строке (столбцу) кратного другой строки (столбца).

Эти преобразования не меняют ранг матрицы. Матрицы, получаемые в процессе преобразования, эквивалентны исходной. В результате элементарных преобразований векторы-строки (столбцы) матрицы можно преобразовать в единичные или в нулевые векторы. Число единичных векторов в преобразованной матрице определяет ее ранг.

2.5. Решение системы линейных уравнений методом Жордана – Гаусса

Рассмотрим систему из т линейных уравнений с n неизвестными:

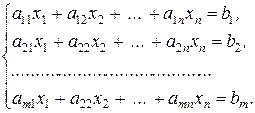
Обозначим через А = (a_ij) матрицу системы, через X =(x_j) - матрицу-столбец, состоящую из неизвестных, через В = ( b_i ) - матрицу-столбец, состоящую из свободных членов; тогда системуможно записать в виде матричного уравнения

AX = B.

При решении системы линейных уравнений воспользуемся численным методом, который позволяет с помощью элементарных преобразований за конечное число шагов найти решение (если оно существует) и при необходимости получить обратную матрицу. Этот метод называется методом полного исключения неизвестных или методом Жордана — Гаусса.

Неизвестное х_к называется разрешенным, если какое-нибудь уравнение содержит х_к с коэффициентом 1, а в остальных уравнениях х_к не содержится.

Суть метода состоит в том, что, рассмотрев первое уравнение, а в нем неизвестное, например, х₁ с коэффициентом а₁₁, отличным от нуля (он в дальнейшем называется разрешающим элементом ), и, разделив первое уравнение на этот коэффициент, с помощью первого уравнения исключают это неизвестное из всех уравнений, кроме первого. Для этого преобразуют систему, умножая обе части 1-го уравнения на а₂₁ и вычитая из соответствующих частей 2-го уравнения. Затем обе части 1-го уравнения умножают на а₃₁ и вычитают из соответствующих частей 3-го уравнения и т.д. Если коэффициент при х ₁ в первом уравнении равен нулю,то можно выбрать любое уравнение, в котором коэффициент при х₁ отличен от нуля, и с помощью этого уравнения исключить х₁ из всех остальных уравнений.

Выбрав во втором уравнении неизвестное с коэффициентом, отличным от нуля, и разделив на него второе уравнение, с помощью второго уравнения исключают другое неизвестное из всех уравнений, кроме второго, и т. д., т. е. с помощью одного уравнения производят полное исключение одного неизвестного. Процесс продолжают до тех пор, пока не будут использованы все уравнения. При этом возможны следующие случаи.

1. В процессе исключений левая часть i- го уравнения системы обращается в нуль, а правая часть равна некоторому числу, отличному от нуля, т. е. имеет место равенство 0=b_i¹0. Это означает, что система несовместна, т.е. не имеет решений.

2. Левая и правая части i-го уравнения обращаютсяв нуль. Это означает, что i-е уравнение является линейной комбинацией остальных, ему удовлетворяет любое найденное решение системы, поэтомуономожет быть отброшено.

3. После того, как все уравнения использованыдля исключения неизвестных, либо будет получено решение,либо доказано, что система несовместна.

Рассмотрим применение метода Жордана — Гауссана примере системы линейных уравнений, в которой количество уравнений меньше количества неизвестных.

Пример 1. Решить системууравнений

или найти коэффициенты разложения вектора В по векторам A₁, А₂, А_3, А₄:

A₁x₁ +А₂x₂ + А₃x₃ + А₄x₄ =B.

Решение. Запишем коэффициенты при неизвестных и свободные члены в таблицу, к элементам которой и применим метод полных исключений.

В первом уравнении коэффициент при x₁ отличен от нуля: a₁₁=5¹0; выбираем его за разрешающий элемент. Разделим первое уравнение на 5. Исключим x₁ из всех уравнений, кроме первого.

А₁ А₂ А₃ А₄ А₀

-2 -2

2/5 -14/5 14/5 3/5 19/5 1/5 3/5 4/5 1/5 1/5 18/5 -13/5

8/7 -19/14 5/7 -2/7 5/7 -9/7

3/7 3/56 1/4 3/7 -53/56 1/4

Выделены разрешающие элементы уравнений, с помощью которых производим полные исключения неизвестных. Окончательно система принимает вид

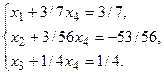
Откуда находим общее решение: х₁ = 3/7-3/7x₄,

x₂ =- 53/56-З/5б х₄,

x₃ = 1/4-1/4x₄.

Общее решение системы – это равносильная разрешенная система, в которой разрешенные неизвестные выражены через свободные.

Векторы A₁, А₂, А₃линейно независимые и составляют базис в трехмерном пространстве; соответствующие им неизвестные x₁, х₂, х₃ называются базисными, а х₄, соответствующее вектору A₄ - свободным (ему можно придавать произвольные значения).

Минор, состоящий из коэффициентов при базисных неизвестных в линейно независимых уравнениях, называется базисным минором.

Любые m переменных системы линейных уравнений с n переменными (m<n) называются базисными, если определитель (базисный минор) матрицы коэффициентов при них отличен от нуля, остальные n-m переменных называются свободными (небазисными).

Базисными могут быть разные группы из n переменных. Максимально возможное число групп равно числу сочетаний .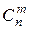

Если в общем решении системы свободные неизвестные приравнять нулю, то такое решение называется базисным.

Таким образом, базисное решение рассматриваемой системы таково: х₁ = 3/7, х₂= - 53/56, x₃ = 1/4, x₄ = 0.

Для базисного решения получаем разложение вектора B по векторам базиса A₁, А₂, А₃

3/7A₁ - 53/56А₂ + 1/4А₃ = B.

Базисное решение, содержащее точно т отличных от нуля неизвестных, где т — количество линейно независимых уравнений системы, называется невырожденным.

Если хотя бы одно из базисных неизвестных равно нулю, то базисное решение называется вырожденным.

Решение X=(x₁,x₂,…,x_n) называется допустимым, если оно содержит лишь неотрицательные компоненты, т.е. x_j³0 для любых j=1,2,…,n. В противном случае решение называется недопустимым.

В ЗЛП особый интерес представляют допустимые базисные решения, называемые опорными планами.

На методе Жордана-Гаусса основаны все известные варианты симплексных методов и, в частности, симплексный метод, который рассматривается ниже.

Контрольные вопросы