Рассмотрим ЗЛП в случае, когда система ограничений задана в виде неравенств и количество неизвестных переменных равно двум, т.е. n=2. Найти экстремальное значение линейной функции L=c1x1+c2x2 при ограничениях 
(1)
x1 ³ 0, x2 ³ 0. (2)
Теорема. Множество решений неравенства с двумя переменными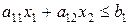 
является одной из полуплоскостей, на которые вся плоскость делится прямой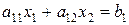 
, включая и эту прямую. А другая полуплоскость с той же прямой есть множество решений неравенства 
.
|
Доказательство. Для произвольной абсциссы х1 ордината точки М, лежащей на прямой 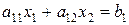, при условии а12¹0, есть 
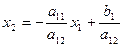, т.е. координаты точки М 
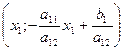. Через точку М проведем прямую, параллельную оси Ох2. Тогда для любых точек Р и Q этой прямой, расположенной выше и ниже точки М, т.е. в верхней и нижней полуплоскостях, будут верны неравенства x2Q³x2M и x2Q £x2M ил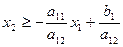и 
и 
. При условии а12>0 неравенства преобразуются соответственно к виду 
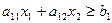(*) и 
(**),
т.е. координаты всех точек верхней полуплоскости удовлетворяют неравенству (**), а нижней полуплоскости – неравенству (*). В случае а12<0, наоборот, координаты всех точек верхней полуплоскости удовлетворяют неравенству (*), а нижней полуплоскости – неравенству (**).¨
Учитывая, что множество точек, удовлетворяющих уравнению
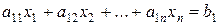
при n=3, является плоскостью, а при n>3 – ее обобщением в n-мерном пространстве - гиперплоскостью, то теорему можно распространить на случай трех и более переменных.
Теорема. Множество всех решений линейного неравенства с n переменными
является одним из полупространств, на которые все пространство делится плоскостью или гиперплоскостью 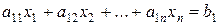, включая и эту плоскость (гиперплоскость).
(без доказательства).
Рассмотрим на плоскости x10x2 совместную систему линейных неравенств (1). Каждое неравенство данной системы геометрически определяет полуплоскость ограниченную прямой ai1x1+ai2x2=bi (i=1,2,...,m). Условия
неотрицательности определяют полуплоскости соответственно с граничными прямыми x1=0 и x2 = 0. Предположим, что система совместна, тогда полуплоскости, как выпуклые множества, пересекаясь, согласно теореме о пересечении выпуклых множеств, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы.
Совокупность этих точек (решений) называется многоугольником решений.
Если рассмотреть задачу ЛП при n=3, то каждое неравенство геометрически представляет полупространство трехмерного пространства, граничная плоскость которого ai1x1 + ai2x2 + ai3x3 = bi (i=1,2,...,m), а условия неотрицательности - полупространства с граничными плоскостями соответственно xj = 0 (j=1,2,3).
Если система ограничений совместна, то эти полупространства, как выпуклые множества, образуют в трехмерном пространстве общую часть, которая называется многогранником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.
Пусть в системе ограничений n>3; тогда каждое неравенство определяет полупространство n-мерного пространства с граничной гиперплоскостью
ai1x1 + ai2x2 +…+ ainxn = bi (i=1,2,...,m), а условия неотрицательности - полупространства с граничными гиперплоскостями соответственно xj = 0 (j=1,2,…,n).
Если система ограничений совместна, то по аналогии с трехмерным пространством она образует общую часть n-мерного пространства, называемую многогранником решений, т.к. координаты каждой его точки являются решением.
Таким образом, геометрически ЗЛП представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции минимальное значение, причем допустимыми решениями являются все точки многогранника решений.
