Задача об использовании ресурсов (планирование производства, задача оптимального использования удобрений и т.д.).
При выпуске n видов продукции используются m видов сырья. Обозначим через
Si (i=1,2,...,m) - виды сырья;
bi - запасы сырья i-го вида;
Pj (j=1,2,....n) - виды продукции;
aij - количество единиц i-го сырья, идущего на изготовление единицы j-й продукции;
Cj - величина прибыли, полученная при реализации единицы j-й продукции. Все данные можно свести в таблицу (см. табл. 1.).
| Вид сырья | Запас сырья | Количество единиц i-го сырья, идущего на изготовление единицы j-й продукции | |||
| P1 | P2 | ... | Pn | ||
| S1 | b1 | a11 | a12 | ... | a1n |
| S2 | b2 | a21 | a22 | ... | a2n |
| ... | ... | ... | ... | ... | |
| Sm | bm | am1 | am2 | ... | amn |
| Прибыль от единицы продукции в грн. | C1 | C2 | ... | Cn |
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Пусть xj - количество единиц j-й продукции, которую необходимо произвести.
Тогда математическая модель задачи имеет следующий вид: найти максимальное значение линейной функции L=C1x1+C2x2+×××+Cnxn (1) при ограничениях:
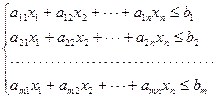 (2)
(2)
xj ³ 0, (j=1,2,×××,n), bi ³ 0 (i=1,2, ×××,m). (3)
Элементы таблицы aij образуют матрицу, имеющую m строк и n столбцов, показывающую количество единиц i-го сырья, идущего на изготовление единицы j-й продукции, которую назовем технологической матрицей и обозначим через A; количество bi ресурсов выразим вектором B=(b1,b2,...,bm) (вектор ресурсов). Назовем планом производства вектор X=(x1,x2,...,xn), показывающий, какие количества товаров P1,P2,...,Pn будут произведены. Цены на продукты производства обозначим как вектор C=(C1,C2,...,Cn).
Представленная модель, хотя и отражает определенные черты реального производства, тем не менее, сильно идеализирована. Так в ней отсутствует такое важное для производства понятие, как время. Считается также, что все необходимые ресурсы S1,S2,...,Sm в нужный момент находятся под рукой. Тем самым мы абстрагировались от острых проблем динамики производства и ритмичности поставок. Здесь также не учитываются затраты живого труда и целый ряд других показателей.
К этому же классу задач относится задача оптимального использования удобрений.
Пусть для выращивания некоторой культуры применяется m видов удобрений соответственно в количестве bi (I=1,2,…,m) единиц. Вся посевная площадь разбита на n почвенно-климатических зон по dj (j=1,2,…,n) единиц. Пусть aij количество i-го удобрения, вносимого на единицу площади j-ой зоны, а Сj – повышение средней урожайности, получаемой с единицы площади j-й зоны. Составить такой план распределения удобрений между посевными зонами, который обеспечивал бы максимальный суммарный прирост урожайности культуры.
Обозначим через xj (j =1,2,…,n) площадь j-й зоны, которую необходимо удобрить, тогда, математическая модель задачи имеет следующий вид:
найти максимальное значение линейной функции L= 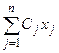 при ограничениях:
при ограничениях:  , i=1,2,…,m, 0£xj£dj, j=1,2,…,n.
, i=1,2,…,m, 0£xj£dj, j=1,2,…,n.
Пример1. Для изготовления двух видов продукции P1, P2 используются 4 вида сырья (ресурсов) S1, S2, S3, S4. Запасы сырья, количество единиц сырья, затраченных на изготовление единицы продукции, а также величина прибыли, полученной от реализации одной единицы продукции, приведены в таблице 2.
Необходимо составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
Таблица 2.
| Вид сырья | Запас сырья | Количество единиц сырья на одну единицу продукции | |
| P1 | P2 | ||
| S1 | |||
| S2 | |||
| S3 S4 | - | - | |
| Прибыль от единицы продукции в грн. |
Решение. Составим экономико-математическую модель задачи.
Определяя через x1 количество единиц продукции P1, через x2 - количество единиц продукции P2, получим систему ограничений:
 x1 ³ 0, x2 ³ 0 (4)
x1 ³ 0, x2 ³ 0 (4)
которая показывает, что количество сырья, расходуемое на изготовление продукции, не может превысить имеющихся запасов. Если P1 не выпускается, то
x1 = 0, иначе x1 > 0. То же самое и для P2, x2 = 0 или x2 > 0. Следовательно, на x1 и x2 должно быть наложено ограничение неотрицательности: x1 ³ 0, x2 ³ 0.
Конечную цель решаемой задачи - получение максимальной прибыли при реализации продукции, выразим как функцию двух переменных x1 и x2: L=2x1 + 3x2 (грн) (5).
Таким образом, задача принимает следующий вид: необходимо найти максимальное значение линейной функции (5) при ограничениях (4).






