Задача №1. Построить график функции у=х3-3х.
При построении графиков функций удобно действовать по следующей схеме:
1. найти область определения функции;
2. установить, обладает ли функция симметрий (исследовать функцию на четность);
3. исследовать функцию на непрерывность, периодичность;
4. рассмотреть поведение функции в окрестностях точек разрыва;
5. определить поведение функции в бесконечности;
6. найти точки пересечения графика функции с осями координат, если это возможно (хотя бы приближенно);
7. найти интервалы возрастания, убывания и точки экстремума функции;
8. определить точки перегиба;
9. определить интервалы выпуклости и вогнутности;
10. составить сводную таблицу и построить график.
В ходе построения графика по мере необходимости можно получить допольнительно ряд значений функции при некоторых частных значениях аргумента х, т.е. еще ряд точек графика. Разумеется, в процессе исследования функции не обязательно строго придерживаться приведенной схемы, иногда даже удобно изменить порядок действий.
Решение.
1. Функция определена при всех 
2. На концах интервала lim (x3-3x)=-¥; lim (x3-3x)=+¥,
x® -¥ x®+¥
3. Определим интервалы возрастания и убывания функции. Функция возрастает на интервале, если f ¢(x)>0. В данном случае f ¢(x)=3х2-3>0, если х2>1 или |х|> 1. Следовательно, функция у=х2-3х возрастает на интервалах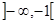 
и 
Функция убывает на интервале, если f ¢(x)<0: 3х2-3<0, откуда х2<1, или -1<х<1. Следовательно, функция у=х3-3х убывает на интервале ]-1, 1[.
4. Определим критические точки и исследуем их характер. Из условия 
(x)=3x2-3=0 найдем критические точки: х1=-1, х2=1. Определим знак первой призводной в окрестностях точек х1=-1, х2=1. Для точки х1=-1 имеем 
, f ¢(x)=3·02-3<0. Так как знак производной при переходе через критическую точку х=-1 изменился с плюса на минус, то х=-1 это точка максимума. Максимум функции f(-1)=(-1)3-3(-1)=2 (точка А на рис. 4). Для точки х2=1 имеем 
, 
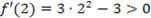. Так как знак производной при переходе через критическую точку изменился с минуса на плюс, то х=1 это точка минимума. Минимум функции 
(точка В на рис. 4).
5. Определим точку перегиба: 
. Ордината точки перегиба f(0)=03-3·0=0 (точка О на рис. 4).
6. Определим интервалы выпуклости и вогнутности. Кривая выпукла при условии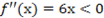 
, откуда х<0. Следовательно, кривая выпукла на интервале 
. Кривая вогнута при условии 
, откуда х>0. Следовательно, кривая вогнута на интервале 
.
7. Найдем точки пересечения кривой с осью Ох. Из системы уравнений 
находим точки пересечения:
0); О (0; 0), 
0).
8. Сведем результаты исследования в таблицу:
| х | -1 | 
| 
| ||
| f(x) | -2 | ||||
| -3 | ||||
| -6 | ||||
| Характер точки | Максимум | Перегиб | Минимум |
9. Строим график функции у=х3-3х
 |
Рис 4. График функции у=х3-3х.
Задача 2. Установить, при каком процентом содержании у кислорода в газовой смеси скорость окисления азота будет максимальной, если уравнение кинетики имеет вид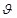 
=k(100x2-x3), где k -постоянная, х -концентрация окиси азота и х+у=100.
Решение. Найдем производную функции 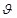и приравняем ее нулю: 
= k(200х-3х2)=0, откуда критические точки х1=0, х2=200/3. Исследуем точку х1=0: 
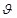В точке х1=0 функция имеет минимум. Исследуем точку х2=200/3: 
Следовательно, х2=200/3 – точка максимума функции 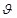, и поэтому у2=100-200/3=33,3. Скорость окисления будет максимальной в том случае, когда в смеси будет содержаться 33,3% кислорода.
Задача 2. Реакция организма на введенный лекарственный препарат может выражаться в понижении температуры, повышении давления и т.д. Степень реакции зависит от назначенной дозы лекарства. Пусть х обозначает дозу назначенного лекарственного препарата, а степень реакции описывается функцией у=f(x)=x2(a-x), где а -положительная постоянная. При каком значении х реакция максимальна?
Решение. Найдем производную функции и приравняем ее к нулю: 
откуда критические точки х1=0, х2=2а/3.
Значение х1=0 указывает на то, что в организм лекарство не вводилось. Исследуем точку х2=2а/3: 
Следовательно, в точке х2=2а/3 функция имеет максимум. Таким образом, х=2а/3 – это доза, которая вызывает максимальную реакцию.
ПРАКТИЧЕСКАЯ ЧАСТЬ