Позиционные и метрические задачи

Под позиционными задачами следует понимать определение взаимного положения элементов: параллельны, пересекаются, принадлежат, не имеют общих точек и т.д.

Под метрическими задачами следует понимать измерение расстояний и углов между элементами, а также определение внутренних размеров элементов: длин, углов, площадей и т.д.

Пример: Построить прямую f, которая пересекает прямые m, n, e (рис. 41).

Если 3 точки принадлежат одной прямой, то они лежат в одной плоскости. Составим систему уравнений:

D(e,R) - плоскость, заданная одной из прямых e и произвольной точкой R

n - вторая заданная прямая

m - третья заданная прямая

Для решения этой системы составим 2 системы уравнений:

D(e,R) Решив систему, определим точку В, которая будет принадлежать

n прямой f.

D(e,R) Решив систему, определим точку A, которая будет принадлежать

m прямой f.

Точки А и В определят прямую f, после чего останется решить систему:

f (А,В) После решения этой системы уравнений определим точку С,

e в которой прямая f пересекает прямую e.

Графическое решение задачи:

- Точку R(R₁,R₂) взяли исходя из условия, что проекции прямых m и n пересекают проекцию плоскости D(RGQ). Точки G(G₁, G₂) и Q(Q₁, Q₂) на прямой е взяли произвольно.

- Известным способом нашли точку пересечения А(А₁,А₂) прямой m(m₁, m₂) с плоскостью D(RGQ) (в плоскости D(RGQ) взяли прямую d, фронтальная проекця d₂ которой совпадает с фронтальной проек-цией m₂, пересечение горизонталь-ных проекций определит горизон-тальную проекцию А₁, А₂ - на пересечении линии связи с m₂).

- Тем же способом определили точку пересечения В(В₁,В₂) прямой

Рис. 41 n(n₁, n₂) с плоскостью D(RGQ).

- Две точки А и В задают прямую f(f₁,f₂). f₁(А₁, В₁), f₂(А₂,В₂).

- Прямые f и е расположены в плоскости D и пересекаются в точке С(С₁,С₂).

Пример: Через точку А провести отрезок АВ длиной 40 мм, который перпендикулярен прямой t и наклонен к плоскости П₁под углом 25° (рис. 42)

Рис.42

Отрезок АВ принадлежит плоскости D, которая проходит через точку А и перпендикулярна прямой t. Такую плоскость можно задать пересекающимися в точке А прямыми h(h₁^t₁, h₂÷÷ Х₁₂) перпендикулярна t(t₁, t₂) и f(f₁÷÷ Х₁₂, f ₂^ t₂) перпендикулярна t(t₁, t₂).

Далее следует выяснить максимальный угол наклона прямых плоскости D к П₁. Он равен углу наклона плоскости D к плоскости П₁. Если a_max > 25°, то отрезок АВ в плоскости D можно построить.

В положении 1 изменен угол b плоскости D(h, f) до 90°, т.к. h ^ П₂(h¹₁ перпендикулярна оси Х₁₂, Н¹₂ – точка. Угол a плоскости D равен

56,8° больше 25°, следовательно, условие задачи можно выполнить.

Далее через точку А¹ построим отрезок А¹В¹(А¹₁В¹₁, А¹₂В¹₂) c углами b=0, a=25° и длиной 40 мм. Этот отрезок не принадлежит плоскости D, поэтому следует ввести точку В в плоскость без изменения координаты Z, для чего повернем ее вокруг оси i_Z ^ П₁ (см. рис. 3, i_Z проходит через А¹). Горизонтальная проекция траектории точки В¹ - окружность r₁ радиусом R=А¹₁В¹₁. Фронтальная проекция дуги r₂ - прямая Z = Z ^В.

Если точка В² принадлежит плоскости D, то ее фронтальная проекция В²₂ принадлежит ее фронтальному следу D_2,т. к. D ^ П₂. Горизонтальная проекция В²₁ точки будет лежать на горизонтальной проекции дуги r₁ и линии связи из В²₂ к оси Х.

Остается вернуть отрезок АВ в исходное положение:

- В положении 1 в плоскости D(h, f) провели прямую 12, пересекающую прямую А¹В² в точке 3. Сначала построена горизонтальная проекция 1¹₁2¹₁ и определена горизонтальная проекция 3¹₁ точки пересечения горизонтальных проекций прямых А¹В² и 1¹2¹.

- Построена фронтальная проекция 1¹₂2¹₂ и определена фронтальная проекция 3¹₂ точки 3.

- Определена фронтальная проекция 1₂2₂ прямой (1₂ расположена на f ₂ и на линии связи к оси Z, 2₂ – на h₂ и на линии связи к оси Z) и фронтальная проекция точки 3₂ (3¹₂ находится на пересечении 1₂2₂ и линии связи к оси Z).

- Определена горизонтальная проекция прямой 12 (1₁ расположена на f₁ и на линии связи к оси Х, 2₁ – на h₁ и на линии связи к оси Х).

- Горизонтальная проекция точки 3₁ находится на пересечении 1₁2₁ и линии связи к оси Х).

- Фронтальная проекция В₂ находится на пересечении на пересечении линии связи к оси Z через В²₂ с продолжением фронтальной проекции прямой А₂3₂. Горизонтальная проекция В₁ расположена в точке пересечения линии связи к оси Х через В₂ с продолжением горизонтальной проекции прямой А₁3₁.

Отрезок АВ перпендикулярен прямой t, наклонен к плоскости П₁под углом 25° и имеет длину 40 мм.

Если проанализировать решение позиционной задачи 1 и позиционно-метрической задачи 2, то легко обнаружить общий подход к решению любой задачи. Он не отличается от известных математических методов решения систем уравнений, которые предполагают выражение одних неизвестных через другие и сокращение таким образом числа уравнений в системе.

Изменять положение объекта в пространстве можно другими способами преобразования чертежа.

На рис.30 определен угол j между фронтальным и горизонтальным следами плоскости D методом вращения вокруг линии уровня.

Линия уровня - прямая, параллельная одной из плоскостей проекций.

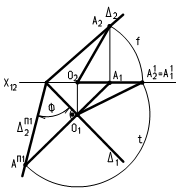В данном случае вращение плоскости D до положения, параллельного П₁, выполнено вокруг прямой D₁, уравнение которой Z=0. Поскольку D₁Ì П₁, то D будет совмещена с плоскостью П₁.

Центр вращения О точки А, принадлежащей D₂, находится на перпендикуляре АО, опущенном из А к оси D₁. На основании (9) А₁О₁ ^ (D₁)₁=D₁. О₂ находится на (D₁)₂ = Х₁₂ и линии связи к оси Х из О₁.

Рис.30 Если угол a наклона плоскости равен 0, то А^П1О₁= êАО ê. Для определения êАО ê изменена координата Z точки А до 0. Дугой f отложен отрезок О₂А¹₂= О₂А₂. Дугой t отложен отрезок А^П1О₁ = О₁А¹₁ = êАО ê. А^П1 - совмещенное с плоскостью П₁ положение точки А. D^П1₂ - совмещенное с плоскостью П₁ положение следа D₂. Угол j = (D^П1₂)^Ù(D₁).

Выше изменение углов наклона объектов к плоскостям проекций выполнено вращением самих объектов.

Те же операции можно выполнять изменением положения плоскостей проекций - методом замены плоскостей проекций.

Такой метод предполагает ввод дополнительных плоскостей проекций, перпендикулярных одной из уже существующих на чертеже и расположенных под определенным углом к объекту.

Если принять, что все нечетные плоскости за исключением 3-ей - горизонтальные, все четные плоскости - фронтальные, 3-я плоскость - профильная, то координаты X, Y, Z определяются в соответствии с равенствами (5).

На рис. 31 определены угол наклона треугольника к плоскости П₁a и его натуральная величина.

Для определения угла a введена дополнительная фронтальная плоскость П₄, которая ^ П₁ и (АВС). Ось x ₁₄ = П₁ Ç П₄. Она проведена ^ прямой АD, которая параллельна П_1.Следовательно, на основании (10) A₁D₁ ^ x ₁₄. Поскольку координаты Z точек А, В, С не изменялись, т.е. горизонтальная плоскость П₁и треугольник АВС не меняли взаимного положения, то проекции точек А, В, С на плоскость П₄ расположены на линиях связи к оси x ₁₄ и удалены от последней на величину прежних координат Z, т.е. ç x ₁₄A₄ç=ç x ₁₂A₂ç, ç x ₁₄B₄ç=ç x ₁₂B₂ç, ç x ₁₄C₄ç=ç x ₁₂C₂ç.

В новой системе координат, заданной плоскостями П₁ Ç П_4,Y^A = ç x ₁₄A₁ç, Y^B = ç x ₁₄B₁ç, Y^C = ç x ₁₄C₁ç.

Проекция треугольника (А₄В₄С₄) - линия пересечения (АВС) с плоскостью проекций П₄.

Угол наклона треугольника (АВС) к плоскости проекций П₁ a = x ₁₄ ^Ù(А₄В₄С₄).

Для определения натуральной величины треугольника (АВС) введена дополнительная горизонтальная плоскость П₅ ^ П₄и параллельная (АВС). Ось x ₄₅ параллельна (А₄В₄С₄), т.е. координаты Z точек А, В и С равны Z^A=ç x ₄₅A₄ç, Z^В=ç x ₄₅В₄ç, Z^С=ç x ₄₅С₄ç.

Положение треугольника (АВС) по отношению к плоскости П₄ не изменилось. Следовательно, горизонтальные проекции точек А₅, В₅, С₅ расположены на линиях связи к оси x _45,проходящих через фронтальные проекции А₄, В₄, С₄, и удалены от оси x ₄₅на величину предыдущих координат Y:

ç x ₁₄A₁ç=ç x ₄₅A₅ç, ç x ₁₄B₁ç=ç x ₄₅B₅ç, ç x ₁₄C₁ç=ç x ₄₅C₅ç.

Проекция (А₅В₅С₅) = çАВСç.

Рис. 31

Способ замены плоскостей проекций прост для понимания и удобен при ручном исполнении чертежа, но в машинном исполнении потребуется оператор преобразования осей координат, который отсутствует в большинстве графических пакетов.