Прямоугольная система координат

 

Приняв прямую за единственный элемент для моделирования трехмерного пространства, можно тремя пересекающимися в одной точке и не лежащими в одной плоскости прямыми образовать трехмерное пространство, обеспечивая измерение в трех направлениях.

В прямоугольной системе координат три прямые x, y и z взаимно перпендикулярны и пересекаются в одной точке БТ, которая совпадает с началом координат 0 (рис. 3).

Для работы в системе необходим аппарат, который позволял бы определять и изменять положение объекта в этом пространстве, т.е. измерять и изменять расстояния и углы.

Если принять точку А за базу параллепипеда S, то положение его в пространстве можно определить расстояниями базы А до плоскостей П₁, П₂, П₃ и углами наклона граней к тем же плоскостям.

 

 

Прямые ix, iY и iz образуют внутреннюю прямоугольную систему координат объекта Σ с началом в точке А. Внутреннюю систему координат объекта можно вращать вокруг ее осей вместе с объектом. При этом будут меняться углы наклона граней объекта к П₁, П₂, П₃.

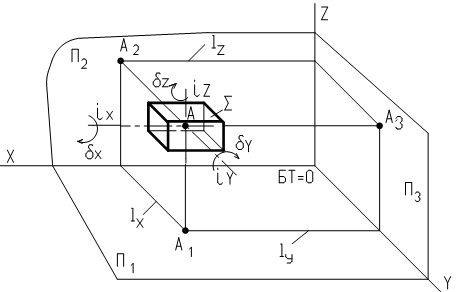Рис. 3. Σ – объект; ix ^ П₃; iY^ П₂; iz ^ П ₁; dх, d_Y; dz – направления вращения

 

Представленная на рис.3 объемная модель трехмерного пространства наглядна, но трудоемка в исполнении и на ней искажены расстояния и углы. Поэтому в конструкторской документации используется плоская модель, которая исключает указанные недостатки.

 

Для формирования модели введем определения:

 

- точка A - пересечение двух линий, обозначается

прописной буквой латинского алфавита; (1)

 

- плоскость Σ - две пересекающиеся прямые, обозначается

прописной буквой греческого алфавита; (2)

 

- отрезок (AB) – участок прямой между двумя точками. (3)

 

В соответствии с определением (2):

- прямые x и y образуют горизонтальную плоскость П₁ (рис. 4а);

- прямые x и z образуют фронтальную плоскость П₂ (рис. 4б);

- прямые y и z образуют профильную плоскость П₃ (рис. 4 в).

Плоскости П₁, П₂, П₃ называются основными плоскостями проекций, т.е. на них будем изображать расположенный в пространстве объект, например, точку А. При этом объект находится между наблюдателем и плоскостью проекций.

Изображение объекта на плоскость - проекция объекта, обозначается именем объекта с индексом плоскости, на которой он изображен. А₁ - горизонтальная проекция точки А, А₂ - фронтальная, А₃ - профильная.

Чтобы получить проекцию точки, достаточно из нее опустить перпендикуляр на плоскость. Точка пересечения перпендикуляра с плоскостью - проекция точки на соответствующую плоскость.

После дополнения первоначальной модели трехмерного пространства тремя плоскостями П₁, П₂ и П₃ положение точки в пространстве будет определено расстояниями до плоскостей проекций:

 

½ АП₂½ = ½ АА₂½ - длина;

½ АП₃½ = ½ АА₃½ - ширина; (4)

½ АП₁½ = ½ АА₁½ - высота.

 

В математике уравнение точки А(X, Y, Z), где X, Y, Z - координаты, в нашей модели длины отрезков, измеренные от БТ вдоль координатных осей x, y и z.

Чтобы совместить равенства (4) c координатами, введем понятие линии связи. Это ломаная линия, соединяющая две проекции одной точки, лежащая в плоскостях проекций и перпендикулярная одной из осей x, y, z. Обозначается латинской буквой l с индексом оси, к которой она перпендикулярна. На рис. 3 l_x - линия связи к оси x, l _y - к оси y, l_Z - к оси z.

Тогда, если обозначить начало координат 0, равенства (4) можно расширить:

½АП₁½ = ½АА₁½ = ½ A₂X ½ = ½A₃Y½ = ½0 l _Z½ = Z

½АП₂½ = ½AA₂½ = ½ A₁X ½ = ½A₃Z½ = ½0 l _Y½ = Y (5)

½АП₃½ = ½AA₃½ = ½A₁Y½ = ½A₂Z½ = ½ 0 l _X ½ = X

 

Cледовательно, положение точки в пространстве может быть определено не только расстояниями до плоскостей проекций, но и отрезками по осям x, y, z от 0 до линии связи: ½0 l _X½ = X; ½0 l _Y½ = Y; ½0 l _Z½ = Z, а также отрезками линий связи от проекции точки до соответствующей оси (½A₁Y₁½ = Х; ½А₂ х ₁₂½ = Z; ½A₁ x ₁₂½ = Y).

Каждая плоскость П₁, П₂ и П₃ может быть изображена на чертеже как две пересекающиеся оси (рис. 4).

Индексы 1, 2, 3 у осей x, y, z определяют принадлежность к соответствующей плоскости проекций П₁, П₂, П₃.

Рис.4. a - горизонтальная плоскость П₁; б - фронтальная плоскость П₂;

в - профильная плоскость П_3.

 

Если три изображения рис. 4 совместить (наложить одно на другое), то получим плоскую модель прямоугольной системы координат (рис. 5).

Оси x, y и z для различных плоскостей проекций совпадают, но отличаются линейным или угловым направлением.

Такая модель не имеет объема, следовательно, в ней не может быть изображен сам объект. Изображается только то, что расположено в плоскости проекций: проекции объекта и линии связи.

В математической модели трехмерного пространства точка задана уравнением A(X, Y, Z), где X, Y, Z - координаты точки соответствуют длинам отрезков Х = n,

Рис. 5 Y=k, Z=m (рис. 5).

 

Уравнения проекций точки A: A₁(X,Y); A₂(X,Z); A₃(Y,Z). Тогда горизонтальная проекция A₁ и фронтальная проекция A₂ имеют одну и ту же координату X, т.е. они принадлежат множеству точек X = n. По определению выше - это линия связи к оси x (l_x). Она удалена от 0 на величину n и перпендикулярна оси X.

По аналогии можно утверждать, что фронтальная проекция A₂ и профильная A₃ принадлежат линии связи к оси z (l_z), которая задана уравнением Z = m, а A₁

 

и A₃ принадлежат линии связи к оси y (l_Y), которая задана уравнением Y = k.

В реальной системе координат y ₁ и y ₃ одна и та же ось y, а в плоской модели y ₁ и y ₃ имеют различное угловое направление, то линия связи также разделена на 2 части l _y1 (расположена на плоскости П₁) и l _y3 (расположена на плоскости П₃). При этом расстояние от начала отсчета вдоль оси y для обеих ветвей одинаково и равно k.

Дуга t означает, что расстояние k, отложенное по оси y ₁ с некоторой степенью точности, перенесено на ось y ₃ c той же погрешностью. Дуга t не принадлежит линии связи и ее можно заменить прямой под углом 45°. В обеих случаях точка пересечения l _y1 с осью y ₁ будет перенесена на ось y ₃, через эту точку пройдет линия связиl _y3 к оси y ₃.

Проекции точки A₁, A₂, A₃ будут находиться на пересечении соответствующих линий связи, что соответствует определению точки (1).

 

Пример: Построить точку В(-20, -15, 25).

 

Построить точку - значит построить ее проекции в прямоугольной системе координат В(В₁, В₂, В₃).

Если горизонтальная и фронтальная проекции имеют одинаковую координату х, то они лежат на одной линии связи к оси x (рис. 6). Для построения точки отложим по оси x координату X = -20 и проведем l_X. Используя равенства (5), отложим на линии связи расстояние ½ x ₁₂В₂½ = Z = 25, получим фронтальную проекцию В₂. На той же линии связи отложим расстояние ½ x ₁₂В₁½ = Y = -15, получим горизонтальную проекцию В₁.

Профильную проекцию В₃ следует получить на пересечении линий связи к осям z и y (l _Z Ç l _y3 ), т. к. измерение одной и той же величины следует вести один раз, чтобы избежать

повторной погрешности измерения

Рис. 6 координат Z и Y.

 

Если заданы проекции точки, то положение ее в реальном пространстве, например, в комнате, где расположен наблюдатель, можно описать следующим образом:

- поскольку координата X отрицательная, то точка находится за боковой стеной;

- поскольку координата Y отрицательная, то точка находится за фронтальной стеной;

- поскольку Z положительная, то точка находится над полом.

 

Положение объекта в пространстве определено, если есть проекции его на 2 плоскости, например, П₁ и П₂ (рис. 7), т.е. известны координаты X = ½0 l_X ½, Y = ½C₁ x ₁₂½, Z = ½C₂ x ₁₂½.

Рис. 7

 

Прямая линия

 

Прямая в прямоугольной системе координат задается положением ее текущей базы, например, точкой A(X, Y, Z) и углами наклона к плоскостям проекций a к П₁, b к П₂, g к П₃ (рис. 8).

 

Угол наклона прямой к плоскости измеряется между

самой прямой и ее проекцией на эту плоскость (6)

 

Под самой прямой на плоской модели будем подразумевать проекцию, длина которой равна модулю. (7)

На основании (6): угол a = (MN)^(M₁N₁);

угол b = (MN)^(N₂M₂);

угол g = (MN)^(M₃N₃).

В прямоугольном треугольнике АВ⁰В катет АВ⁰ равен длине горизонтальной проекции А₁В₁, катет ВВ⁰ равен разности координат ½Z^A-Z^B½.

Отсюда:

- длина горизонтальной проекции A₁B₁ = AB ´ Cos(a);

- угол наклона к плоскости П₁ a = arctg(½Z^A - Z^B½ / A₁B₁). (8)

 

Управляющим параметром для изменения угла наклона прямой a является разность координат Z концов отрезка. Следствием изменения a будет изменение длины горизонтальной проекции.

Если рассмотреть аналогичные треугольники для углов b и g, то:

 

- длина фронтальной проекции A₂B₂ = AB ´ Cos(b)

- угол наклона к плоскости П₂ b = arctg(½Y^A - Y^B½ / A₂B₂) (9)

 

Управляющим параметром для изменения угла наклона прямой b является разность координат Y концов отрезка. Следствием изменения b будет изменение длины фронтальной проекции.

 

- длина профильной проекции A₃B₃ = AB ´ Cos(g)

- угол наклона к плоскости П₃ g = arctg(½X^A - X^B½ / A₃B₃) (10)

 

Управляющим параметром для изменения угла наклона прямой g является разность координат Х концов отрезка. Следствием изменения g будет изменение длины профильной проекции.

Рис. 8

Если a = 0, то горизонтальная проекция А₁В₁=½АВ½ и может быть принята за длину прямой.

Если b = 0, то фронтальной проекция А₂В₂ =½АВ½ и может быть принята за длину прямой.

 

Если g = 0, то профильной проекция А₃В₃=½АВ½ и может быть принята за длину прямой.

 

В плоской модели прямая задана проекциями (рис. 9).

Рис.9

Проекции заданы линейными уравнениями на плоскостях П₁, П₂ и П₃:

 

Y = K₁ · X + C₁ - горизонтальная проекция А₁В₁; (11)

Z = K₂ · X + C₂ - фронтальная проекция А₂В₂; (12)

Z = K₃ · Y + C₃ - профильная проекция А₃В₃, (13)

где:

K₁=tq(j1); K₂=tq(j2); K₃=tq(j3); С₁ - координата Y точки A; C₂ = C₃ - координата Z точки A.

Следовательно, в плоской модели задано положение текущей базы прямой A(X, Y, Z), но отсутствуют углы a, b, g и модуль ½АВ½.

 

Линии пересекаются, если они расположены в одной плоскости. Следовательно, пересекаться могут только одноименные проекции: горизонтальные с горизонтальными, фронтальные с фронтальными, профильные с профильными.

 

На рис. 9 определены точки пересечения прямой АВ с плоскостями проекций – следы прямой. Горизонтальный след М – точка пересечения прямой с плоскостью П₁. Она определена из условия, что координата Z точки

равна нулю (точка М принадлежит горизонтальной плоскости П₁, все точки которой имеют координату Z =0). Если продолжить фронтальную проекцию A₂B₂ до пересечения с фронтальной проекцией оси Х, которая совпадает с осью Х₁₂, то в результате будет получена фронтальная проекция точки М₂.

Иначе – решена система линейных уравнений:

Z=Tg (j₂)X + Z^A (фронтальнаяпроекция A₂B₂)

Z=0 (фронтальная проекция оси Х).

В результате решения системы уравнений получена координата Х точки М.

Горизонтальная проекция М₁ будет на пересечении линии связи к оси Х с продолжением горизонтальной проекции прямой А₁В₁. Иначе – решена система линейных уравнений:

Y=Tg (j₁)X + Y^A(горизонтальнаяпроекция A₁B₁)

Х=Х^М(линия связи к оси Х через М₂).

В результате решения системы уравнений получена координата Y точки М.

N – точка пересечения с плоскостью П₂. Она определена из условия, что координата Y такой точки равна нулю, для чего горизонтальная проекция A₁B₁ продолжена до пересечения с горизонтальной проекцией оси Х, совпадающая с осью Х₁₂. Точка пересечения - горизонтальная проекция точки N₁.

Иначе – решена система линейных уравнений:

Y=Tg (j₁)X + Y^A (горизонтальная проекция A₁B₁)

Y=0 (горизонтальная проекция оси Х).

В результате решения системы уравнений получена координата Х точки N.

Фронтальная проекция N₂ будет на пересечении линии связи к оси Х и продолжении фронтальной проекции прямой А₂В₂. Иначе – решена система линейных уравнений:

Z=Tg (j₂)X + Z^A(фронтальнаяпроекция A₂B₂)

Х=Х^N(линия связи к оси Х).

В результате решения системы уравнений получена координата Z точки М.

P – точка пересечения с плоскостью П₃. Она определена из условия, что координата Х такой точки равна нулю (Рис. 8). Горизонтальная проекция Р₁ находится на пересечении горизонтальной проекции прямой А₁В₁ и оси Y. Профильная проекция Р₃ и совпадающая с ней Р находятся на пересечении профильной проекции А₃В₃ и линии связи к оси Y.

 

Обозначения: АВ – прямая в исходном положении; А¹В¹ – прямая в первом текущем положении; А²В² - прямая во втором текущем положении и т. д.;

А₁В₁ – горизонтальная проекция прямой в исходном положении; А¹₁В¹₁ – то же в первом текущем положении; А²₁В²₁ – во втором текущем положении;

 

А₂В₂ – фронтальная проекция прямой в исходном положении; А¹₂В¹₂ – то же в первом текущем положении; А²₂В²₂ – во втором текущем положении и т. д.

Угол a наклона прямой к плоскости П₁ (рис. 10) равен углу между фронтальной проекцией прямой АВ, если она равна ее натуральной величине, и горизонтальной проекцией. Для чего согласно (9) следует выравнять координаты Y точек А и В, что возможно, если j1=0, тогда Y^A = Y^B, как следствие: b=0, А²₂В²₂=½АВ½. С изменением угла b не меняются длина горизонтальной проекции (А²₁В²₁) = (A₁B₁) и координаты Z точек А и В, т.к. они не входят в формулы (9), на основании которых выполнено изменение угла b. Формально угол a измерен между А²₂В²₂=½АВ½ и горизонтальной прямой (А²₂ А₂), параллельной А²₁В²₁.

Рис. 10

 

В реальном трехмерном пространстве (согласно рис. 3) второе текущее положение прямой А²В² получено:

- изменены координаты X и Y точки А без изменения координаты Z (в результате точка А переместилась влево и вперед по отношению к исходному положению, расстояние точки А до горизонтальной плоскости проекций не изменилось);

- горизонтальная проекция А₁В₁прямой АВ повернута по часовой стрелке вокруг оси iz на угол j₁ (см. рис. 9), в результате АВ стала параллельна плоскости проекций П₂.

Управляющим параметром изменения угла a является разность½ Z^A - Z^B½. Изменение разности координат Z ведет к изменению угла a.

 

Угол b наклона прямой к плоскости П₂ (рис. 10) равен углу между горизонтальной проекцией прямой АВ, если она равна ее натуральной величине, и фронтальной проекцией. Для чего согласно (8) следует выравнять координаты Z точек А и В, что возможно, если j2=0, тогда Z^A = Z^B, как следствие: a=0, А¹₁В¹₁=½АВ½. С изменением угла a не меняются длина фронтальной проекции (А¹₂В¹₂) = (A₂B₂) и координаты Y точек А и В, т. к. они не входят в формулы (8), на основании которых выполнено изменение угла a. Формально угол b измерен между А¹₁В¹₁=½АВ½ и горизонтальной прямой (А¹₁ А₁), параллельной А¹₂В¹₂.

В реальном трехмерном пространстве (согласно рис. 3) первое текущее положение прямой А¹В¹ получено:

- изменены координаты X и Z точки А без изменения координаты Y (в результате точка А переместилась вправо и вниз по отношению к исходному положению, расстояние точки А до фронтальной плоскости проекций не изменилось);

- фронтальная проекция А₂В₂ прямой АВ повернута по часовой стрелке вокруг оси iY на угол j₂ (см. рис. 9). В результате АВ стала параллельна плоскости проекций П₁.

Управляющим параметром изменения угла b является разность½Y ^A -Y ^B½.

Изменение разности координат Y ведет к изменению угла b.

Пример. Увеличить угол наклона прямой CD к горизонтальной плоскости проекций на 22° и длину на 20 мм (рис. 11).

 

Изменять размер любого элемента можно при условии, что на чертеже он выполнен в натуральную величину. Поэтому:

1. В 1-ом текущем положении прямой C¹D¹(C¹₁D¹₁, C¹₂D¹₂) (запись означает, что прямая C¹D¹ задана горизонтальной и фронтальной проекциями) определим натуральную величину угла a = 12°.

2. На основании (8) при увеличении угла aуменьшается длина горизонтальной проекции С₁D₁, следовательно, максимальному значению угла aбудет соответствовать минимальная длина горизонтальной проекции С₁D₁. Увеличивать угол aв исходном положении прямой CD можно вращением ее вокруг оси iY (см. рис. 3), проходящей через точку С. Вращаться будет точка D. Траектория движения фронтальной проекции D₂ – окружность h₂, горизонтальная проекция h₁ траектории движения D₁ – прямая, заданная уравнением Y=Y^D.

 

Минимальная длина горизонтальной проекции прямой в положении CD⁷(C₁D⁷₁, C₂D⁷₂) равна (C₁D⁷₁) = DY. Дальнейшее уменьшение длины приведет к изменению разности ½Y ^A -Y ^B½ и угла b, что не предусмотрено условиями решаемой задачи.

В результате определена координата Z = Z^D7 точки D при a^маx. Траектория движения фронтальной проекции D¹₂ – дуга t, следовательно, фронтальная проекция D²₂ при a^маx будет на пересечении дуги t и прямой D⁷₂D²₂, которая задана уравнением Z = Z^D7(D⁷₂D²₂). a^маx = 47° измерен между (C¹₂ D²₂) и прямой, заданной уравнением Z = Z^С1 и параллельной (C¹₁ D²₁). Длина горизонтальной проекции (C¹₁ D²₁) = DY.

После увеличения исходного угла a=12° на 22° суммарный угол 34° меньше a^маx = 47°.

Рис. 11

 

Для построения прямой CD после изменения угла проведем фронтальную ее проекцию через C¹₂ под углом 34° до пересечения с дугой t в точке D³₂. В результате получим фронтальную проекцию (C¹₂ D³₂). Горизонтальная проекция точки D³₁ находится на линии связи к оси Х и на горизонтальной

 

 

проекции прямой. В исходном положении фронтальная проекция D⁵₂ находится на пересечении фронтальной проекции дуги h₂ и линии связи к оси Z через D³₂ (линейное уравнение Z=Z^D3). Горизонтальная проекция D⁵₁ расположена на линии связи к оси Х и на горизонтальной проекции дуги h₁.

Прямая C D⁵(C₁D⁵₁, C₂ D⁵₂) наклонена к плоскости П₁ под углом 34°.

Контрольный размер – радиус дуги f, равный C₁D⁵₁, на основании (8) равен C¹₁ D³₁ т. к. a_const.

Чтобы увеличить длину CD на 20 мм, увеличим длину фронтальной проекции (C¹₂ D³₂) = ½CD½. В результате получим фронтальную проекцию точки D⁴₂, горизонтальная проекция D⁴₁ будет расположена на пересечении горизонтальной проекции прямой с линией связи к оси Х. В исходном положении фронтальная проекция D⁶₂ находится на продолжении фронтальной проекции C₂D⁵₂ и на линии связи к оси Z, проходящей через D⁴₂. Горизонтальная проекция D⁶₁ расположена на продолжении горизонтальной проекции C₁D⁵₁ и на линии связи к оси Х.

Прямая C D⁶(C₁D⁶₁, C₂ D⁶₂) наклонена к плоскости П₁ под углом 34° и ее длина увеличена на 20 мм.

Примечание: Любая проекция точки – результат решения системы двух уравнений.

 

Плоскость

 

В общем виде плоскость задана двумя пересекающимися прямыми (2). Если на этих прямых взять 3 точки, не лежащие на одной прямой, то плоскость будет задана тремя точками. Если 3 упомянутые точки соединить прямыми, то плоскость будет задана треугольником (плоской фигурой в том числе окружностью, проходящей через три точки). Если через точку на первой прямой провести прямую, параллельную второй прямой, то плоскость будет задана двумя параллельными прямыми.

На рис.12 и 13 плоскость Q задана следами Q₁, Q₂, Q₃. След плоскости – линия пересечения плоскости с соответствующей плоскостью проекций.

Горизонтальный след Q₁ расположен в плоскости П₁ и имеет 3 проекции: горизонтальная проекция (Q₁)₁ совпадает с самой прямой Q₁; фронтальная (Q₁)₂ совпадает с осью Х (линейное уравнение Z=0); профильная (Q₁)₃ совпадает с осью Y.

 

Фронтальный след Q₂ расположен в плоскости П₂ и имеет 3 проекции: фронтальная проекция (Q₂)₂ совпадает с самой прямой Q₂; горизонтальная (Q₂)₁ совпадает с осью Х (линейное уравнение Y=0); профильная (Q₁)₃ совпадает с осью Z.

Профильный след Q₃ расположен в плоскости П₃ и имеет 3 проекции: профильная (Q₃)₃ совпадает с самой прямой Q₃; фронтальная (Q₃)₂ совпадает с осью Z (линей

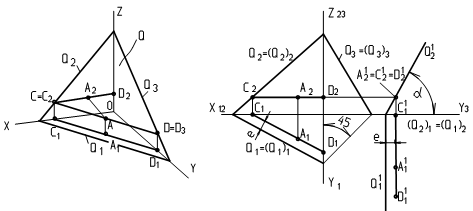ное уравнение Х=0); горизонтальная (Q₃)₁ совпадает с осьюY. Точки пересечения следов расположены на соответствующих осях x,y и z _.

Рис. 12 Рис. 13

В плоскости (рис. 12) изображена прямая СD, точка С принадлежит Q₂, точка D принадлежит Q₃. Угол a наклона прямой СD равен 0. C₁D₁ – горизонтальная проекция прямой, С₂D₂ – фронтальная.

 

Точка принадлежит плоскости, если она

принадлежит прямой, лежащей в этой плоскости (14)