
Точка может принадлежать прямой, в этом случае на плоском чертеже проекции точки принадлежат соответствующим проекциям прямой. На рис. 16 точки А(А1,А2) и В(В1.В2) принадлежат прямой f(f1,f2), т. к. А1, В1 принадлежат f1 и А2, В2 принадлежат f2.
Рис. 16
Точки C и D по той же причине не принадлежат прямой f (обе проекции точки D не принадлежат одноименным проекциям прямой f, горизонтальная проекция C1 не принадлежит горизонтальной проекции f1).
Прямая f и две точки С и D образуют жесткий объемный объект, например двугранный угол между плоскостями D(АВD) и S(АВС), который имеет неизменные внутренние размеры, например расстояния от точек С и D до прямой f (высоты треугольников с общим основанием АВ). Следовательно, изменять положение в пространстве любого элемента (например, отрезка прямой АВ) можно только вместе с другими элементами (точками C и D).
Если расстояние измеряется между двумя точками, то определить
расстояние от точки до прямой можно при условии, что проекция прямой – точка. Для чего угол наклона отрезка прямой АВ к горизонтальной плоскости проекций в текущем положении 2 изменен до 90°.
Изменять угол a (АВ) можно при наличии его натуральной величины. Поэтому в положении 1 определен ÷a (АВ)÷, для чего на основании (9) и (11) тригонометрический угол горизонтальной проекции j1 изменен до 0°. Координата YА при этом изменении j1 стала равна координате YВ и угол наклона к фронтальной плоскости проекций b(АВ) стал равен 0°, фронтальная проекция А12В12 = ÷АВ÷, угол÷a (АВ)÷ = А12В12 Ù А11В11.
Чтобы сохранить геометрические размеры горизонтальной проекции объекта при изменении угла j1 в текущем положении 1, в исходном положении из горизонтальных проекций точек C1 и D1 опустим перпендикуляры C1К и D1Н на горизонтальную проекцию прямой А1В1. Для построения в первом текущем положении горизонтальной проекции точки С11 от горизонтальной проекции точки А11 отложено расстояние (А11 К) = (А1 К), из точки К восставлен перпендикуляр (КС11) = (КС1). Для построения горизонтальной проекции точки D11 от горизонтальной проекции точки А11 отложено расстояние (А11Н) = (А1Н), из точки Н восставлен перпендикуляр (НD11) = (Н D1).
Фронтальные проекции точек А12 , В12 , С12 и D12 расположены на пересечении линий связи к оси Х через проекции точек А11 , В11 , С11 и D11 и линий связи к оси Z через проекции точек А2 , В2 , С2 и D2.
В текущем положении 2 угол a изменен по отношению к текущему положению 1 на угол (90 - a)° и стал равен 90°. Горизонтальная проекция прямой – точка А21= В21.
Геометрические размеры фронтальной проекции во 2 текущем положении должны соответствовать геометрическим размерам той же проекции в 1 текущем положении. Положение фронтальной проекции точки D22 определено расстояниями от концов фронтальной проекции отрезка (А22 В22) и находится на пересечении дуг радиусами R=(А12 D12 ) и R=(В12 D12 ). Аналогично построена фронтальная проекция точки С22.
Горизонтальные проекции точек D21, С21 расположены на пересечении линий связи к оси Х через проекции D22, С22 и линий связи к оси Y через проекции D11, С11.
Примечание: Оба варианта сохранения геометрических размеров проекции объекта при перемещении в новое текущее положение равнозначны.
Расстояние от точки D до прямой f(f1,f2) определяется во 2 текущем положении между горизонтальной проекцией точки D21 и горизонтальной проекцией прямой (А21= В21). Расстояние от точки С до прямой f(f1,f2) - ÷ С21, (А21= В21)÷.
Взаимное положение прямых
Параллельные прямые имеют одинаковые углы наклона к плоскостям проекций, но расстояние между ними не равно 0 (базовая точка одной прямой не принадлежит другой прямой). На рис. 17 прямая a(a1, a2)и параллельная ей прямая е(е1, е2) заданы проекциями на плоскости П1 и П2. Линейные уравнения:
Ya = K1´ X + YВ - горизонтальная проекция прямой a
Yе = K1´ X + YС - горизонтальная проекция прямой е
Za = K2 ´ X + ZB - фронтальная проекция прямой a
Zе = K2 ´ X + ZС - фронтальная проекция прямой е.
Одноименные проекции параллельны (a1êêе1,a2êêе2), т. к. коэффициенты К1, К2 в одноименных уравнениях одинаковы.
 Рис. 17
Рис. 17
Для определения расстояния между параллельными прямыми a и e достаточно изменить угол наклона прямых, например к плоскости П2, до 90°. Тогда фронтальные проекциями прямых A22 и E22 на П2 будут точки, расстояние между этими точками равно расстоянию между параллельными прямыми ½a,e½ = ½A22E22½.
Пересекающиеся прямые имеют общую точку, проекции которой лежат на одной линии связи к оси x и совпадают с точками пересечения одноименных проекций, угол между прямыми j больше 0 (рис. 18).
Для определения угла между пересекающимися прямыми следует исходить из того, что они задают плоскость S(n, m). Тогда для определения угла j достаточно например, изменить угол наклона плоскости S к пл. П1 до 0, и горизонтальная проекция угла между горизонтальными проекциями m21 и n21 будет равна натуральной величине угла между прямыми m и n. Для этого следует:
- в плоскости S выделить треугольник (АВС) с вершиной в точке А(n Ç m), основание треугольника ВС следует взять исходя из условия, что угол aВС = 0, что возможно, если ZB = ZC, в этом случае угол bВС = В1С1 ^ В2С2;
Рис. 18 
- в первом текущем положении угол наклона прямой bВС увеличен до 90°, в результате треугольник (АВС) стал перпендикулярен П2, угол наклона его к горизонтальной плоскости проекций aАВС измеряется между S2 и осью Х12;
- во втором текущем положении угол a(АВС) изменен до 0° (координаты ZA=ZB=ZC), горизонтальная проекция треугольника (А21В21С21) = ½АВС½, угол (В21 А21С21) = (m^ n) = j.
 |
Скрещивающиеся прямые - не пересекаются (расстояние между ними не равно 0), не параллельны (угол между ними не равен 0). На плоском чертеже точки пересечения одноименных проекций не лежат на одной линии связи к оси x (рис. 19).
Рис.19
При определении расстояния и угла между ними следует исходить из условия, что через две скрещивающиеся прямые можно всегда провести две параллельные плоскости.
Плоскости параллельны, если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся
прямым другой плоскости. (18)
Расстояние между скрещивающимися прямыми формально равно расстоянию между параллельными плоскостями S и D, которые проведены через скрещивающиеся прямые.
Угол между ними равен углу между пересекающимися прямыми, которые построены в одной из упомянутых плоскостей параллельно скрещивающимся прямым.
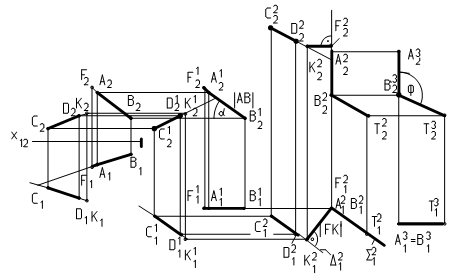
Кратчайшее расстояние можно измерить между двумя точками, например между принадлежащей прямой АВ точкой F и точкой К, которая является основанием перпендикуляра, опущенного из точки F на прямую CD. При этом точка F не может быть произвольной. Однозначно можно взять проекцию точки на проекции прямой, если проекция прямой – точка.
Поэтому:
- определим угол наклона a прямой АВ к плоскости П1 в текущем положении 1, для чего выравняем координаты Y точек А и В (тригонометрический угол наклона горизонтальной проекции А11В11 j1 = 0° Þ bАВ = 0 Þ (А12В12) = ½АВ½ Þ aАВ = ½АВ½^ (А11В11));
- во 2 текущем положении угол aАВ увеличен до 90°, фронтальная проекция (A22В22) ^ Х12 , горизонтальная проекция (А21=В21) – точка;
- горизонтальная проекция точки F21, из которой следует опустить перпендикуляр на прямую CD для измерения кратчайшего расстояния между прямыми, совпадет с горизонтальной проекцией (А21=В21) прямой АВ.
Прямая параллельна плоскости, если она параллельна прямой,
которая принадлежит плоскости. (19)
Прямая перпендикулярна плоскости, если она перпендикулярна
двум пересекающимся прямым в этой плоскости. (20)
Проекция прямого угла - прямой угол, если одна из его сторон
параллельна плоскости проекций. (21)
Во 2 текущем положении построена параллельная прямой CD плоскость S, которая задана пересекающимися прямыми (АВ Ç АТ). На основании (19) прямая АТêê CD Þ фронтальные проекции (A22Т22) êê (С22D22) и горизонтальные проекции (A21Т21) êê (С21D21). Плоскость S перпендикулярна плоскости П1 согласно (16), т. к. АВ ^ П1. Следовательно, горизонтальный след плоскости S21 совпадет с горизонтальной проекцией прямой (A21Т21). Угол наклона плоскости S к фронтальной плоскости проекций П2 bS = S21 ^ Х12.
Если через прямую СD построить плоскость D параллельную S, то горизонтальный след D21 совпадет с горизонтальной проекцией прямой (С21D21).
Перпендикуляр, опущенный из точки F на прямую CD, будет одновременно перпендикуляром к плоскости D. В таком случае горизонтальная проекция F21К21 перпендикуляра, опущенного из точки F на прямую CD на
основании (21) перпендикулярна D21. К21 – горизонтальная проекция точки пересечения перпендикуляра с прямой CD. Фронтальная проекция точки К22 находится на пересечении линии связи к оси Х12 с фронтальной проекцией С22D22 прямой CD.
Если прямая FK ^S, то на основании (21) фронтальная проекция прямой F22К22 ^ A22В22 (bАВ=0).
Угол наклона прямой FK к горизонтальной плоскости проекций во 2 текущем положении равен 0 (координаты Z точек F и К одинаковы). Следовательно, расстояние между скрещивающимися прямыми равно длине горизонтальной проекции F21К21 отрезка прямой FK.
Угол между скрещивающимися прямыми АВТ во 2 текущем положении расположен в плоскости S и задан горизонтальной проекцией A21 В21Т21 и фронтальной проекцией A22 В22Т22. Натуральная величина угла j определена в 3 текущем положении, для чего угол bS изменен до 0°. Угол j равен Ð A32 В32Т32 .






