Чтобы выяснить взаимное положение двух плоскостей, следует определить взаимное положение двух пересекающихся прямых, расположенных в первой
- если прямые параллельны второй плоскости, то и плоскости параллельны (рис. 29a);
- если одна прямая пересекает вторую плоскость, а другая параллельна, то линия пересечения плоскостей проходят через точку пересечения первой прямой с плоскостью и параллельна второй прямой (рис. 29б);
- если прямые пересекают вторую плоскость, то точки их пересечения определяют линию пересечения плоскостей (рис. 29 в).
На рис. 29a две пересекающиеся прямые D1 и D2 плоскости D соответственно параллельны двум пересекающимся прямым S1 и S2 плоскости S,
следовательно, плоскости параллельны.
a б в
 |
Рис. 29
На рис. 29б фронтальные следы D2 и S2 плоскостей D и S параллельны, а горизонтальные следы D1 и S1 пересекаются в точке 1(11,12). Если плоскости содержат параллельные между собой прямые D2 и S2, то линия пересечения плоскостей е параллельна этим прямым (фронтальная проекция е 2ïï(D2)2 = D2 и е 2ïï (S2)2 = S2, горизонтальная проекция е1ïï(D2)1 = Х12 и е 1ïï (S2)1 = Х12) и проходит через общую для плоскостей точку 1.
На рис. 29 в плоскости имеют 2 общие точки: 1(11,12) - точка пересечения фронтальных следов D2 и S2 и 2(21,22) - точка пересечения горизонтальных следов D1 и S1. Прямая 12(1121, 1222) – линия пересечения плоскостей.
В случае параллельности плоскостей следует определить расстояние между ними, а в случае пересечения - угол между ними.
Для этого достаточно изменить угол наклона плоскостей к П1 или к П2 так, чтобы одна из них стала перпендикулярна плоскости проекций. Взаимное положение плоскостей при этом не должно изменяться, т.к. они составляют единый объект.
На рис. 30 заданы плоскости D(ABC) и S(t½½EF). Для определения взаимного положения плоскостей в текущем положении 1 изменим угол a плоскости D до 90°. С этой целью в плоскости D(ABC) взяли прямую ВD c углом b = 0. Угол a прямой ВD равен В2D2ÙB1D1. Угол поворота жесткой системы плоскостей D и S по часовой стрелке вокруг оси iY, которая проходит через точку В (см. рис. 3), равен 90°-a После поворота фронтальная проекция В12D12 ^ Х12. Плоскость D станет перпендикулярна П1, горизонтальная
проекция А12В12С12 совпадет с горизонтальным следом D11. В нашем конкретном случае горизонтальная проекция плоскости S E11F11R11 совпадет с горизонтальным следом S11, следовательно, плоскость S перпендикулярна П1, одновременно горизонтальные следы плоскостей параллельны (D11½½S11), следовательно, плоскости тоже параллельны. Расстояние между плоскостями будет равно расстоянию между параллельными прямыми - следами D11 и S11.
 |
Рис. 30
На рис. 31 заданы плоскости S(ABC) и D(D1,D2). Для определения их взаимного положения изменили угол b горизонтального следа плоскости до 90° (в первом текущем положении D11 ^ Х12). Плоскость D стала ^ П2. В нашем конкретном случае плоскость S не перпендикулярна П2 (фронтальная проекция А12В12С12 не спроецировалась в прямую линию).
Фронтальная проекция любой прямой, лежащей в плоскости D, совпадает с D12, в том числе и фронтальная проекция линии пересечения плоскостей E12R12 совпадет с D12. Плоскости пересекаются.
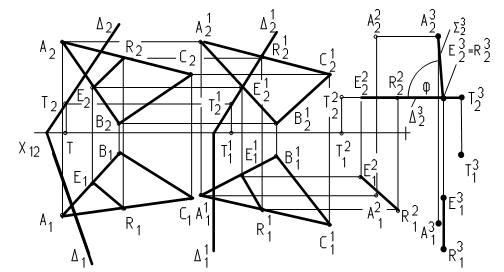Рис. 31
Для определения угла между плоскостями D и S достаточно на основании (15) изменить угол наклона линии пересечения плоскостей, например, к плоскости П2 до 90°. Тогда обе плоскости на основании (16) будут перпендикулярны П2.
Если задать плоскость D прямой ER и точкой T, которая принадлежит D, а плоскость S - ER и точкой A, принадлежащей S, то при изменении углов наклона плоскостей изменять положение будут прямая ER и точки A и Т.
В текущем положении 2 определен угол наклона линии пересечения ER к плоскости П2. bЕR = E21R21 ^ E22R22.
В текущем положении 3 плоскости D(ER, Т) и S (ER, A) перпендикулярны П2, bЕR=90°, а угол между плоскостями j = S32 ^ D32.
