Властивість предметів мати протяжність називається довжиною. А також довжиною відрізка називається додатна величина, яка визначається для кожного відрізка так, що:
1) рівні відрізки мають рівні довжини;
2) якщо відрізок складається із кінченої кількості відрізків, то його довжина дорівнює сумі довжин цих відрізків.
Розглянемо процес вимірювання довжин відрізків. З множини відрізків вибирають будь-який відрізок e і приймають його за одиницю довжини. На відрізку а від одного його кінця відкладають послідовно відрізки, що дорівнюють e до тих пір, поки це можливо. Якщовідрізки, що дорівнюють e, відкладаються n раз і кінець останнього співпав з кінцем відрізка а, то кажуть, що значення довжини відрізка а – це натуральне число n і пишуть: а = nе.
Якщо ж відрізки, що дорівнюють e відклалися n раз і ще залишилась остача, яка менша e, то на ній відкладають відрізки, що дорівнюють
e1 = 
e.
Якщо вони відклалися точно n1 раз, тоді а = n,n1е і значення довжини відрізка а – цескінчений десятковий дріб.
Якщо відрізок e1 відклали n1 раз і залишилась остача, яка менша e1 , то на ній відкладають відрізки, що дорівнюють
е2 = 
e.
Якщо цей процес продовжувати далі, то отримаємо, що значення довжини відрізка а – це нескінченний десятковий дріб.
Отже, при вибраній одиниці довжина будь – якого відрізка виражена додатнім дійсним числом.
Правильне і обернене твердження:
якщо дано додатне число n,n 1 n 2 …, то при побудові відрізка його числове значення довжини буде рівне дробу n,n 1 n 2...
Отже, маємо основну властивість довжин відрізків:
при вибраній одиниці довжини довжина будь-якого відрізка виражена додатнім дійсним числом і, навпаки, для кожного додатного дійсного числа існує відрізок, довжина якого виражена цим числом.
Зауважимо, що коли в результаті вимірювання маємо нескінчений десятковий дріб, то значення довжини відрізка вважається наближеним.
Сформулюємо інші властивості довжин відрізків:
1. Якщо два відрізка рівні, то числові значення їх довжин теж рівні і, навпаки, якщо числові значення довжин двох відрізків рівні, то і рівні самі відрізки, тобто
а = b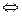 
me (a) = me (b).
2. Якщо даний відрізок – це сума декількох відрізків, то числове значення його довжини дорівнює сумі числових значень довжин відрізків-доданків і, навпаки, якщо числове значення довжини відрізка дорівнює сумі числових значень декількох відрізків, то і сам відрізок дорівнює сумі цих відрізків, тобто
с = а + b 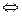me (с) = me (a) + me (b).
3. Якщо довжини відрізків а і b такі, що b = х · а, де х – додатне дійсне число і довжина відрізка а виміряна за допомогою одиниці е, то для того, щоб знайти числове значення довжини відрізка b при одиниці е, достатньо число х помножити на числове значення довжини відрізка а при одиниці е, тобто
b = х · а 
me (b) = х · me (а).
4. При зміні одиниці довжини числове значення довжини збільшиться (або зменшиться) в стільки ж разів, в скільки збільшиться (або зменшиться) нова одиниця відносно старої.
З даних властивостей маємо:
5. а < b 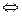mе (а) < mе (b),
а > b 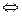mе (а) > mе (b);
6. с = а − b 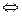me (с) = me (a) − me (b);
7. х = а: b х = me (a): me (b).
Розглянуті властивості дозволяють порівнювати довжини відрізків та дії над ними зводити до порівняння та дій над відповідними числовими значеннями довжин цих відрізків.
Приклади:
1) 15м < 15, 1м, бо 15 < 15, 1;
2) 6, 5см + 4, 8см = (6, 5 + 4, 8) см = 11, 3см;
3) 14 · 2 дм = (14 · 2) дм = 28дм.
Найдавніші одиниці довжини ототожнювались з назвами частин людського тіла. Наприклад: ширина чотирьох пальців – долоня, довжина ліктя – лікоть, довжина ступні – фут, довжина суглоба великого пальця – дюйм, довжина фаланги вказівного пальця – вершок.
У XV – XVI ст. у ряді країн були одиниці, пов’язані між собою. У Росії одиницями довжини були миля, верства, сажень і аршин:
1миля = 7 верств,
1 верства = 500 сажнів,
1 сажень = 3 аршина.
У метричних одиницях 1 аршин ≈ 71,12см.
Основою для міжнародної системи мір стала нова система одиниць вимірювання величин, створена у Франції у 18 столітті. За основну одиницю довжини в цій системі мір було взято метр – одна сорокамільйонна частина довжини земного меридіана, який проходить через Париж. Тому було виготовлено платиновий еталон метра – лінійку з нанесеними штрихами на її кінцях, що зберігається в Національному архіві Франції та має назву «архівного метра».
Метрична система мір не одразу дістала визнання: у 1875 р. нею користувались 17 держав, а зараз – 60. У Росії ця система почала використовуватись з 1899 р., а в Україні – з 1925 р.
При сучасних вимірюваннях довжин використовують такі одиниці як міліметр (мм), сантиметр (см), дециметр (дм), метр (м), кілометр (км), між якими існують відповідні співвідношення:
1м = 100см 1км = 1000м
1м = 10дм 1 дм = 10см
1м = 1000мм 1см = 10мм
