Означення. Якщо кожному елементу х числової множини Х за правилом f відповідає єдине число у, то говорять, що на множині Х задано числову функцію f (х), і пишуть: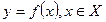 
. При цьому х називають аргументом, а у – значенням функції. Множину Х називають областю визначення функції, а множину значень, які функція набуває, - її множиною значень; останню позначають через f (Х).
Для області визначення і множини значень функції f застосовують також відповідно позначення 
і 
.
Функцію f (х) можна вважати заданою, якщо задано її область визначення Х і правило f, за яким для довільного х з області визначення Х можна знайти (обчислити) відповідне йому значення у, у = f (х).
Останнє правило можна задавати по-різному, що й визначає способи задання функції. Найпоширеніші способи задання функцій такі: аналітичний, табличний та графічний.
Аналітичний спосіб означає задання функції формулою, що показує кількість і послідовність операцій над аргументом х, які необхідні для того, щоб дістати значення 
цієї функції. Якщо при цьому не зазначається область визначення функції, то під останньою розуміють множину допустимих значень аргументу, тобто множину тих значень аргументу, для яких за формулою можна знайти відповідні значення функції.
Табличний спосіб задання функції полягає в написанні таблиці відповідних значень аргументу та функції. Цей спосіб задання функції часто застосовують в експериментальних дослідженнях, а також у математиці: таблиці квадратів і кубів чисел, таблиці значень тригонометричних функцій та ін.
Щоб розглянути графічний спосіб задання функції, розглянемо спочатку поняття графіка функції.
Означення. Графіком функції 
, називають множину точок 
координатної площини, де 
, а 
Графічний спосіб задання функції полягає в тому, що вихідною інформацією про цю функцію є її графік. При цьому для довільного значення х з області визначення Х можна знайти відповідне значення у функції. Прикладом графічного способу задання функції є електрокардіограми, за яким 
и медики аналізують роботу серця.
У математиці графічне зображення функцій використовують і тоді, коли функція задана аналітичним чи табличним способом. Якщо треба з’ясувати загальний характер поведінки функції та її особливості на деяких підмножинах області визначення, графік, завдяки його наочності є дуже корисним.
Найчастіше графіком функції є деяка лінія координатної площини. Проте не кожна лінія є графіком функції. Справа в тому, що при заданому значенні аргументу х існує лише одне відповідне йому значення функції у. Тому на кожній прямій, паралельній осі ординат, може лежати не більше однієї точки графіка функції.
Наприклад, лінія, зображена нижче не є графіком функції.
Лінійна функція
Означення. Лінійною функцією називають функцію виду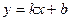 
, де k і b – деякі числа.
Якщо, зокрема, k = 0, то дістають функцію у = b, яку називають сталою.
Областю визначення лінійної функції є множина R.
Графіком лінійної функції є пряма з кутовим коефіцієнтом k і початковою ординатою b.
На рис. зображено графіки л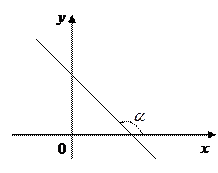 
інійних функцій відповіно для k > 0 і k < 0.
Якщо k > 0, то функція зростаюча, якщо k < 0, то функція спадна.
Наприклад. Задано функцію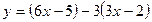 
. Яка це функція? Знайти її область визначення. Чи є вона зростаючою на якій-небудь множині?
Розв’язання. Оскільки 
, то задану функцію можна записати у вигляді: 
; 
.
Отже, задана функція є лінійною. Її областю визначення як лінійної функції є множина R. Оскільки ця функція спадна на R, то вона не може бути зростаючою на будь-якій множині Р.
Пряма пропорційність
Означення. Прямою пропорційністю називають функцію виду 
, де k – деяке число, що не дорівнює нулю.
Число k у формулі називають коефіцієнтом пропорційності.
Пряма пропорційність – це окремий випадок лінійної функції при 
, а 
. Тому справедливі такі твердження:
1. Областю визначення прямої пропорційності є множина R.
2. Пряма пропорційність з додатним (від’ємним) коефіцієнтом пропорційності є зростаючою (спадною) функцією на всій області визначення.
3. Графіком прямої пропорційності є пряма з кутовим коефіцієнтом, що дорівнює коефіцієнту пропорційності, і початковою ординатою, що дорівнює нулю. На рис. зображено графіки прямої пропорційності для 
.
 |  |
4. Для прямої пропорційності відношення двох довільних значень аргументу, що існує, дорівнює відношенню відповідних значень функції: 
.
Для прямої пропорційності з додатним коефіцієнтом із збільшенням (зменшенням) значення аргументу в кілька разів відбувається збільшення (зменшення) значення функції у стільки ж разів.
Наприклад. Точка (2; 4) належить графіку прямої пропорційності. Записати формулу цієї залежності.
Розв’язання. Згідно з означенням прямої пропорційності, шукана формула має вигляд , де k – деяке число, відмінне від нуля. Оскільки точка (2; 4) належить графіку розглядуваної функції, то 
, звідки 
.
Отже, шуканою формулою є 
.
Обернена пропорційність
Означення. Оберненою пропорційністю називається функція виду 
, де k – деяке число, що не дорівнює нулю.
Число k у формулі називають коефіцієнтом оберненої пропорційності.
Областю визначення оберненої пропорційності є множина R \ {0}.
Графіком оберненої пропорційності є гіпербола. На рис. зображено г 
рафіки оберненої пропорційності 
для .
Для оберненої пропорційності відношення двох довільних значень аргументу дорівнює оберненому відношенню відповідних значень функції: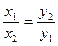 
.
Для оберненої пропорційності з додатним коефіцієнтом збільшенню (зменшенню) аргументу в кілька разів відповідає зменшення (збільшення) значення функції у стільки ж разів.
Наприклад. Знайти формулу оберненої пропорційності, якщо при значенні аргументу х = 2 функція набуває значення у = – 2.
Розв’язання. За означенням оберненої пропорційності шуканою формулою є , де k – деяке число, відмінне від нуля. Оскільки за умовою х = 2 і у = – 2 задовольняють цю формулу, то маємо 
. Звідси 
.
Отже, шуканою формулою є 
.
