Означення. Дві нерівності називаються рівносильними, якщо їх множини розв’язків рівні.
Наприклад, нерівності 
і 
рівносильні, бо їх множини розв’язків рівні і є числовим проміжком 
.
Теореми про рівносильність нерівностей схожі з теоремами про рівносильність рівнянь, і доведення їх аналогічне до доведення теореми 1 рівносильності рівнянь.
Теорема 3. Нехай нерівність f (х) > g (x) задана на множині Х і h (х) – вираз, який визначений на тій же множині Х. Тоді нерівність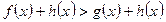 
і дана нерівність f (х) > g (x) рівносильні.
Теорема 4. Нехай нерівність f (х) > g (x) задана на множині Х і h (х) – вираз, який визначений на тій же множині Х і для всіх значень х з множини Х 
. Тоді нерівність 
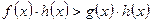і дана нерівність 
рівносильні на множині Х.
Теорема 5. Нехай нерівність f (х) > g (x) задана на множині Х і h (х) – вираз, який визначений на тій же множині Х і для всіх значень х з множини Х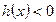 
. Тоді нерівність 
і дана нерівність рівносильні на множині Х.
При розв’язуванні нерівностей з однією змінною першого степеня використовують наслідки з теорем про рівносильність нерівностей.
Наслідки з теорем про рівносильність нерівностей
До теореми 3
1. Якщо до обох частин нерівності додати одне й те саме число, то дістанемо нерівність, рівносильну даній.
2. Якщо в нерівності перенести доданок з однієї частини в другу, змінивши його знак на протилежний, то дістанемо нерівність, рівносильну даній.
До теореми 4
Якщо обидві частини нерівності помножити (або поділити) на одне і те саме додатне число, то дістанемо нерівність, рівносильну даній.
До теореми 5
Якщо обидві частини нерівності помножити (або поділити) на одне і те саме від’ємне число і знак нерівності змінити на протилежний, то дістанемо нерівність, рівносильну даній.
Наприклад.
1. Розв’яжемо нерівність: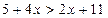 
а) Перенесемо доданок 2 х у ліву частину нерівності, а доданок 5 у праву, змінивши їх знаки на протилежні: 
За наслідком 2 з теореми 3 дістанемо нерівність, рівносильну даній.
б) Виконаємо тотожне перетворення – зведемо подібні: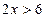 
Дістали нерівність, рівносильну попередній, а отже і даній.
в) Поділимо ліву і праву частини нерівності на число 2: 
За наслідком з теореми 4 дістанемо нерівність, рівносильну попередній, отже і даній.
Отже, розв’язком нерівності є проміжок
 |
2. Розв’яжемо нерівність: 
Розв’язання.
Отже, множиною розв’язків нерівності є проміжок 
 |
У початкових класах розглядаються лише найпростіші нерівності. Вони розв’язуються такими способами: методом підбору; на основі залежностей між компонентами та результатом дій; зведенням нерівності до рівності.
Наприклад. При яких значеннях букви а правильна нерівність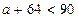 
.
Міркуємо так: зводимо до рівності, рівняння 
перетворюється у правильну рівність при 
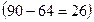. Щоб сума 
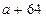була менше 90, потрібно взяти 
(якщо один доданок сталий, а другий зменшити, то і сума зменшиться).
Отже, на множині цілих невід’ємних чисел множиною розв’язків нерівності є множина 
.
