1) Закон існування і єдиності суми.
З означення дробу і означення дії додавання невід’ємних раціональних чисел та закону існування суми і добутку натуральних чисел випливає, що дія додавання дробових чисел завжди здійсненна, тобто, що сума невід’ємних раціональних чисел завжди існує і є число невід’ємне і раціональне.
Наприклад. 1) 
2) 
У цих прикладах знайдено суму, користуючись означенням. Проте дроби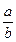 
і 
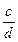можна замінити еквівалентними їм дробами із спільним знаменником по-різному. Чи не зміниться від цього їх сума? Наприклад, дроби 
і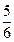 
простіше додати, звівши до найменшого спільного знаменника: 
2) Переставний закон: 
Доведення.
Беручи до уваги переставний закон додавання і множення натуральних чисел, легко зробити висновок про тотожність цих виразів.
3) Сполучний закон: 
Доведення. 
Ці вирази тотожно рівні. Оскільки всі перетворення еквівалентні, то і вихідна рівність є тотожністю.
Дія множення в множині невід’ємних раціональних чисел має ті самі властивості, що й множення натуральних чисел:
1) Існування і єдиність добутку: які б не були невід’ємні раціональні числа 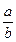, , 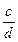завжди існує невід’ємне раціональне число 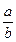· 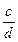, що є їх добутком, і до того ж єдине.
2) Комутативний (переставний) закон: від зміни місць співмножників значення добутку не змінюється: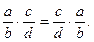 
Доведення. Виконаємо дії у правій і лівій частинах рівності: 
Оскільки для множення цілих невід’ємних чисел має місце комутативний закон, можна зробити висновок, що ці дроби рівні.
3) Асоціативний (сполучний) закон: окремі співмножники можна сполучати в будь-які групи, а потім перемножати. Від цього значення добутку не зміниться: 
4) Монотонність множення: 
5) Дистрибутивний (розподільний) закон відносно додавання і віднімання:
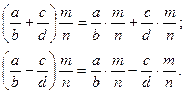
Приклади:
1) 
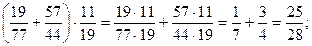
2) 
Упорядкованість множини додатних раціональних чисел
Якщо раціональні числа представлені рівними дробами, то вони рівні.
Наприклад, а = 
, b = 
, то а = b тому, що = .
Як визначити, яке число більше чи менше?
Означення: Нехай а і b – додатні раціональні числа. Тоді а < b, якщо існує таке додатне раціональне число с, що а + с =b.
Для того, щоб різниця додатних раціональних чисел а і b існувала, необхідно і достатньо, щоб b<a.
Відношення «менше» володіє властивостями антисиметричності і транзитивності, тобто є відношенням порядку на множині додатних раціональних чисел, а сама ця множина є упорядкованою множиною.
В множині додатних раціональних чисел:
1) немає найменшого числа;
2) між будь-якими двома різними додатними раціональними числами існує нескінченно багато чисел цієї множини.
