У математиці вивчають не тільки об’єкти, але і зв’язки, відношення між ними.
Наприклад. Відношення у множині чисел: «більше», «більше на», «більше в», «менше»; у множині прямих: «паралельність», «перпендикулярність»; у множині фігур: «рівність», «подібність».
Відношення між двома об’єктами називається бінарним. Ми будемо розглядати тільки бінарні відношення або просто відношення.
Перед нами постає завдання: маючи уявлення про конкретні відношення між числами, геометричними фігурами, множинами та іншими об’єктами, встановити, що спільне є у цих відношень, яким чином можна класифікувати таку велику кількість різноманітних відношень. Знання цього матеріалу потрібно вчителю початкових класів для того, щоб, вивчаючи конкретні відношення в початковій школі, розуміти їх спільність, взаємозв’язки, роль у засвоєнні тих чи інших понять.
Візьмемо множину Х = {2,3,4} і розглянемо деякі відношення між її елементами:
«більше»: «3>2», «4>2», «4>3», маємо пари (3;2), (4;2), (4;3);
«більше на 1»: «3>2 на 1», «4>3 на 1», маємо пари (3;2), (4;3).
Бачимо, що для кожного відношення маємо множину впорядкованих пар. Для відношення «більше» це множина {(3;2), (4;2), (4;3)}, для відношення «більше на 1» - {(3;2), (4;3)}. Ці множини є підмножинами декартового добутку Х×Х = {(2;3), (2;4), (2;2), (3;2), (3;3), (3;4), (4;2), (4;3), (4;4)}.
Означення. Відношенням між елементами множини Х або відношенням, визначеним у множині Х, називають будь-яку підмножину декартового добутку Х×Х, або декартового квадрата Х2.
Відношення позначають великими буквами латинського алфавіту: P, Q, R, S і т.д. Якщо елемент х знаходиться у відношенні R з елементом у, то пишуть так: х R у.
Відношення можна позначати графічно. Для цього в математиці існує поняття графа.
Означення. Графом (від грец. «графо» - пишу) називається креслення, яке складається з точок, що позначають елементи множини, та стрілок, які з’єднують відповідні точки, вказуючи на певне відношення між елементами даної множини.
Наприклад. У множині Х = {2,4,6,8} задано відношення Р: «х < у». Тоді його можна записати Р = {(2;4), (2;6), (2;8), (4;6), (4;8), (6;8)}, або подати за допомогою графа.
Стрілки графа можуть починатися і закінчуватися в одній і тій же вершині, вони називаються петлями. Якщо дві різні точки графа з’єднуються стрілками, напрями яких протилежні, то для спрощення дві стрілки замінюють однією і називають її подвійною.
Наприклад. У множині Х = {2,4,68,12} задано відношення R: «кратне». Тоді його можна записати R = {(2;2), (4;2), (4;4), (6;2), (6;6), (8;2), (8;4), (8;8), (12;2), (12;4), (12;6), (12;12)}, або подати за допомогою графа.
Способи задання відношень
За означенням відношенням між елементами множини Х є будь-яка підмножина декартового добутку Х×Х, тобто множина, елементами якої є упорядковані пари. Тому способи задання відношень такі ж, як і способи задання множин.
1. Відношення у множині можна задати шляхом перелічування всіх пар елементів множини, що знаходяться у цьому відношенні.
Форми запису при цьому можуть бути різними.
Наприклад. Деяке відношення R на множині Х = {3,4,5,6,8} можна задати, записавши множину пар: {(4;3), (5;3), (5;4), (6;3), (6;4), (6;5), (8;3), (8;4), (8;5), (8;6)}.
Те ж відношення можна задати за допомогою графа.
2. Відношення у множині можна задати, вказавши характеристичну властивість всіх пар елементів, що знаходяться у цьому відношенні.
Форми запису також можуть бути різними.
Для попереднього прикладу: відношення R: «число х більше, ніж число у», або коротко R: «більше», або у вигляді нерівності R: «х > у».
Властивості відношень
У математиці вивчають різноманітні відношення між двома об’єктами. Кожне з них розглядається у деякій множині Х і є множиною пар. Таких відношень дуже багато. Чи можна їх класифікувати? Так. Для цього потрібно виділити у відношеннях найбільш характерні їх властивості. Розглянемо деякі з них.
Означення. Відношення R у множині Х називається рефлексивним, якщо кожен елемент множини Х є у відношенні R сам до себе.
R рефлексивне у Х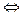 
х R х для будь-якого х Є Х.
Приклади рефлексивних відношень: «паралельність прямих», «рівність», «кратність». Якщо відношення рефлексивне, то в кожній вершині графа є петля.
Відношення «більше», «менше», «перпендикулярності» не є рефлексивними.
Означення. Відношення R у множині Х називається антирефлексивним, якщо кожен елемент множини Х не є у відношенні R сам до себе.
R антирефлексивне у Х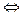 
для будь-якого х Є Х.
Приклади антирефлексивних відношень: «більше». «менше» у числових множинах, «перпендикулярність» - у множині прямих на площині. Якщо відношення антирефлексивне, то в кожній вершині графа відсутня петля.
Означення. Відношення R у множині Х називається симетричним, якщо з того, що елемент х є у відношенні R до елемента у, випливає, що елемент у є у відношенні R до елемента х.
R симетричне у Х 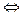х R у 
у R х.
Приклади симетричних відношень: «паралельність», «перпендикулярність», «рівність». Якщо відношення симетричне, то на графі подвійна стрілка.
Відношення «більше». «менше». «довше» не є симетричними.
Означення. Відношення R у множині Х називається антисиметричним, якщо з того, що елемент х не є у відношенні R до елемента у і х≠у, не випливає, що елемент у є у відношенні R до елемента х.
R антисиметричне у Х 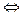х R у і х≠у 
.
Приклади антисиметричних відношень: «більше», «менше», «подільності». Якщо відношення антисиметричне, то на графі стрілка в один бік.
Означення. Відношення R у множині Х називається транзитивним, якщо з того, що елемент х є у відношенні R до елемента у, а елемент у є у відношенні R до елемента z, то елемент х також перебуває у відношенні R до елемента z.
R транзитивне у Х 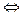х R у і у R х х R z.
Приклади транзитивних відношень: «паралельність», «рівність», «подібність», «кратність».
Як бачимо, різні за змістом відношення можуть мати спільні властивості. Це дає можливість виділяти відношення з певними наборами властивостей. Найважливішими з них є відношення еквівалентності і порядку.
