Способи задання відповідностей

Ми означили, що відповідності – це відношення між елементами двох множин. Тому способи задання відповідностей аналогічні до способів задання відношень.

1 спосіб: перелічування пар елементів.

Наочно це можна зобразити графом, таблицею, графіком (для числових множин);

2 спосіб: характеристичною властивістю пар.

Відповідність між елементами двох множин можна зобразити за допомогою графіка на координатній площині. Для цього на координатній площині позначають всі пари чисел, які знаходяться в даній відповідності. Одержана фігура і буде графіком відповідності.

Справедливе і обернене твердження: будь-яка підмножина точок координатної площини є графіком деякої відповідності.

Побудуємо графіки відповідності «більше» між елементами різних множин (відповідність задана за допомогою характеристичної властивості).

А={3,5,7,9}, В= {4,6}.

Тоді R={(5;4), (7;4), (7;6), (9;4), (9;6)} (відповідність задана перелом пар).

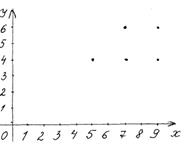Елементи множини А позначимо на осі ОХ, а елементи множини В – на осі ОУ. Кожну із одержаних пар – точкою в системі координат. Одержимо графік відповідності «більше» між елементами множин А і В.

2) А=R, В={4,6}

Множина А нескінченна, в неї входять всі числа, а множина В містить лише два елемента. Між елементами даних множин задано відповідність «більше». З’ясуємо, які числа з множини А більші від числа 4. Всі числа, більші числа 4, розміщені на осі ОХ вправо від точки 4.Отже, всі точки, абсциси яких належать проміжку (4, 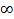), а ординати дорівнюють 4, утворюють промінь. Цей промінь не має початку, оскільки точка (4,4) графіку даної відповідності не належить.

Аналогічно, всі точки, яких абсциса вибирається з проміжку (6, ), а ордината дорівнює 6, утворюють також промінь без початку (6;6).

3) А=R, B=R.

Побудуємо графік відповідності «більше» у випадку, коли множини А і В – нескінчені.

Всі точки, для яких абсциса дорівнює ординаті, лежать на бісектрисі першого і третього координатних кутів. Всі точки, для яких абсциса більша ординати, розміщені під бісектрисою першого і третього координатних кутів.

Отже, графіком відповідності «більше» на множині Х дійсних чисел буде півплощина, розміщена під бісектрисою першого і третього координатних кутів, а сама бісектриса півплощині не належить.

Розглянемо приклад задання відповідності за допомогою таблиць.

Нехай задано дві множини: А = {2,3,6,12} і В = {2,3,4}. Між елементами даних множин встановлено відношення подільності R: числа з множини А діляться на числа з множини В. Математично це можна записати так: , R ={(2;2), (3;3), (6;2), (6;3), (12;2), (12;3), (12;4)}.

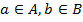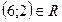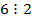Випишемо по вертикалі всі елементи множини А, а по горизонталі – множини В. Якщо пара , де , то на перетині відповідного рядка і стовпця записуємо 1, якщо ні – записуємо 0. Одиниця і нуль тут визначають істинність висловлень про належність пар даній відповідності. Так, у рядку, де міститься елемент 6, є дві одиниці і один нуль. Це означає, що висловлення або , або істинні, а висловлення , - хибне. Таку прямокутну таблицю з нулів і одиниць називають матрицею даної відповідності.

За допомогою таблиць і графів можна задавати лише скінченні відповідності з порівняно невеликою кількістю елементів. Для нескінченних відповідностей такими способами можна ілюструвати лише деякі їхні скінченні частини.