Суть будь-якої класифікації (понять, відношень і т.ін.) зводиться до того, що елементи однієї (універсальної) множини за певними характеристичними ознаками розбиваються на дві або кілька непорожніх підмножин так, щоб кожен елемент даної множини входив в одну і тільки одну з підмножин, тобто щоб ці підмножини попарно не перетинались, інакше, щоб переріз кожної пари з них був порожньою множиною.
Яскравим прикладом класифікації понять є класифікація чисел: множина комплексних чисел поділяється на дві підмножини, що не перетинаються, - множину дійсних чисел і множину уявних чисел. Множина дійсних чисел поділяється на дві підмножини, що не перетинаються, - множину раціональних і множину ірраціональних чисел.
Нехай універсальною множиною є множина натуральних чисел. Візьмемо за основу класифікації властивість, пов’язану з кількістю дільників числа. Тоді множину натуральних чисел розбивають на три підмножини, що попарно не перетинаються:
1) множину натуральних чисел, які мають тільки два дільники: одиницю і самі себе – прості числа Р  N;
N;
2) множину натуральних чисел, які мають більше двох дільників (крім 1 і самого себе мають ще якийсь дільник) – складені числа С  N;
N;
3) одноелементну множину {1}. Число 1 не належить ні до простих чисел, ні до складених, бо має лише один дільник – само себе {1}  N.
N.
Ці три підмножини попарно не перетинаються.

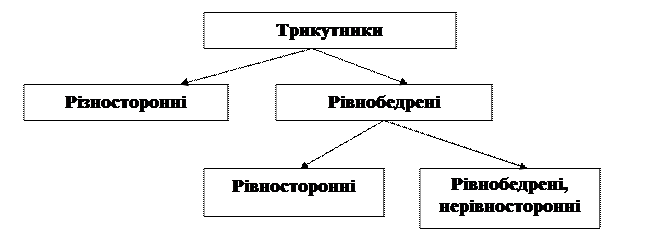
Розглянемо ще приклад класифікації геометричних понять. Нехай універсальною множиною є множина трикутників А. Залежно від рівності сторін множину трикутників поділяють на дві підмножини, перерізом яких є порожня множина: множина В трикутників, у яких є принаймні по дві рівні сторони – рівнобедрені трикутники; множина С різносторонніх трикутників. В свою чергу. Множина В рівнобедрених трикутників поділяється на дві підмножини, що не перетинаються: множина трикутників, у яких тільки дві сторони рівні, це рівнобедрені, але не рівносторонні; множина К трикутників, у яких всі три сторони рівні – рівносторонні.
Для того щоб не допустити при класифікації помилок, які призводять до неправильного розв’язання задач, зокрема рівнянь та нерівностей, слід пам’ятати дві умови:
1) підмножини (жодна пара їх), на які розбиваємо основну множину, не повинні мати спільних елементів, тобто множини їх попарних перерізів повинні бути порожніми: Аi ∩ Aj = ø, і ≠ j;
2) класифікація повинна бути повною, вичерпною. Це означає, що жоден елемент основної множини не повинен залишитись не охопленим однією з множин: А1  А2
А2  А3
А3  …
…  Аk = U
Аk = U
Кількість елементів універсальної множини при розбитті її на підмножини повинна дорівнювати сумі кількостей елементів усіх підмножин:
n (U) = n (A1) + n (A2) + … + n (A k)
Так, наприклад, не можна класифікувати функції на парні і непарні, як це роблять часто учні за аналогією з поділом натуральних чисел, бо окрім парних і непарних функцій є ще функції, які не належать ні до парних, ні до непарних.






