Соответствия между двумя множествами

Изучая окружающий мир, математика рассматривает не только его объекты, но и связи между ними. При выполнении многих ма­тематических и бытовых задач устанавливают связи между двумя множествами, которые называют соответствиями. Например:

• Решите уравнения уравнения →числа, которые являются корнями уравнения).

• Измерьте длину отрезков отрезки → числа, характеризующие их длины).

• Сядьте на свои места (люди → стулья).

Одной из начальных задач математической подготовки детей яв­ляется формирование умения устанавливать соответствия между двумя множествами.

Например, ребенку предлагается задание: «Угости кукол чаем. Дай каждой кукле по чашке. Всем ли куклам хватило чашек?» Вы­полняя это задание, ребенок устанавливает соответствие между множеством кукол и множеством чашек, образовывая пары из эле­ментов данных множеств.

Или такой пример: на пронумерованных стульях разложены куклы: одна, две, ни одной. На рисунке 37 игрушки обозначены буквами А, В, С, D.

Задание: «Назови, на каком по порядку стуле (считая слева направо) какие куклы сидят». Ответы: «На первом стуле сидят А и

 

 

 

При подготовке детей к счетной деятельности особую роль иг­рает умение устанавливать соответствие между двумя множествами «один к одному». Например, детям предлагаются задания:

• Подбери к каждой картинке соответствующую геометриче­скую фигуру. (Наглядный материал: карточки с изображени­ем солнышка, конверта, носового платка и геометрические фигуры из картона: круг, квадрат, прямоугольник.)

• Дай белочкам по одной шишечке. (Наглядный материал: кар­тинки или игрушки, количество которых одинаково.)

Ребенок каждому элементу одного множества ставит в соответ­ствие только один элемент другого множества, охватывая все эле­менты. Такие соответствия называют взаимно однозначными.

Взаимно однозначное соответствие — это соответствие, при кото­ром каждому элементу одного множества соответствует единствен­ный элемент другого множества и каждый элемент второго множес­тва соответствует только одному элементу первого множества.

В процессе формирования счетной деятельности дети учатся устанавливать взаимно однозначное соответствие между отрезком натурального ряда и множеством предметов, которые считают. Отсюда следуют те правила, без которых счет невозможен:

- Каждому предмету соотносить только одно число.

-Каждое число соотносить только одному предмету. Дети, не понимающие этого, совершают ошибки:

• пропускают при счете предметы,

• один и тот же предмет считают дважды,

• пропускают числа,

• одно число повторяют дважды.

Предварительная практическая работа по составлению пар предметов из разных множеств (установление взаимно однозначных соответствий) дает впоследствии возможность осознанно выполнять счет, быстро и правильно сформировать навыки счетной деятель­ности.

Задание 29

Постройте графы четырех различных соответствий между множе­ствами X = {а, Ь, с, d} и У = {1, 2, 3, 4} тан, чтобы одно из них было взаимно однозначным.

Равномощные множества

Еще не умея считать, дети могут определять: поровну ли пред­метов в группах, каких предметов больше, каких меньше. Напри­мер, в процессе установления соответствий между множеством блю­дец и множеством чашек дети рассуждают так: «Если на каждом блюдце есть чашка, значит, чашек и блюдец поровну. Если на од­ном блюдце нет чашки, значит, блюдец больше, чем чашек, а чашек меньше, чем блюдец».

Пусть даны два множества: А = {а, Ъ, с, d } и В = {к, I, т, п. } Не пересчитывая число их элементов, а лишь установив взаимно одно­значное соответствие, можно сказать, что множество А содержит элементов столько же, сколько и множество В. Говорят, что эти множества имеют одинаковую мощность, или они равномощны. Пи­шут А -В.

Множества называются равномощными, если между их элемента­ми можно установить взаимно однозначное соответствие.

Задание 30

Постройте графы взаимно однозначных соответствий, если это возможно, между множествами:

— дней недели и цветов спектра;

— времен года и цветов спектра.

Нетрудно убедиться в том, что если равномощные множества конечны, то они содержат поровну элементов.

Конечные равномощные множества называются равночисленными.

Бесконечные множества могут быть равномощными, например, множество действительных чисел и множество точек прямой, и не равномощными, например, множество натуральных чисел и мно­жество точек прямой.

При сравнении двух групп предметов по количеству приемами наложения или приложения дети по существу устанавливают взаим­но однозначное соответствие между данными множествами (или между одним множеством и подмножеством другого). При этом ис­пользуются термины: «столько же, сколько», «меньше», «больше». Здесь, еще на дочисловом этапе, дети определяют, равномощны множества или нет.

Задание 31

Приведите примеры множеств, равномощных множеству:

— времен года;

— углов у пятиугольника;

— ног у человека.

2.8. Отношения между элементами одного множества

Связи между элементами одного множества в математике назы­вают отношениями.

Отношения очень многообразны, например:

• на множестве людей: «старше», «родиться в одном месяце», «выше», «жить в одном доме», «быть сестрой»;

• на множестве предметов: «быть одной формы», «быть одного цвета», «тяжелее»;

• на множестве понятий: «быть видом», «быть частью»;

• на множестве предложений: «следовать», «быть равносильны­ми»;

• на множестве чисел: «больше», «меньше на I», «быть равны­ми», «следовать за»;

• на множестве прямых: «быть параллельными», «пересекать­ся»;

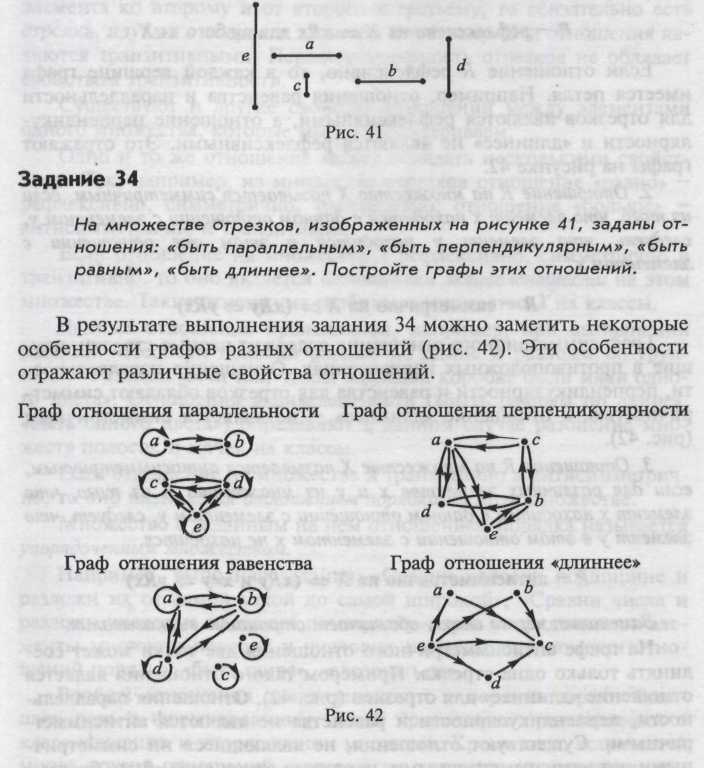
• на множестве отрезков: «длиннее», «короче».

Отношения могут быть заданы и на символическом языке, на­пример, как в задании 32.

 

 

2. Перечисляют все пары элементов, взятых из множества и связанных этим отношением.

Например, элементы множества X = {1, 2, 3, 4, 5} связаны от­ношением «быть больше на 1». В этом случае отношение задано с помощью предложения «число х больше числа у на h. Это же отно­шение можно задать, перечислив все пары чисел, связанных дан­ным отношением: (2,1), (3,2), (4,3), (5,4).

Полезно предлагать детям упражнения, выполняя которые они переходят от одного способа задания отношений на множестве к другому. Например.

1.Вставьте пропущенное число: (1;6), (8;13), (5;10), (7; 12), (3;.,.)-Здесь необходимо сначала выяснить характеристическое свой­ство всех пар чисел, а затем найти пропущенный элемент.

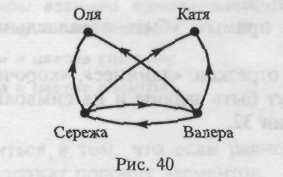
2, «Оля, Катя, Сережа, Валера — дети одних родителей. Назови­те, кто кому является братом».

Выполняя данное упражнение, дети должны перейти от задания отношения с помощью характеристического свойства к перечисле­нию пар элементов.

Данное отношение «быть братом» можно изобразить при помо­щи графа. Все элементы множества изображаются точками, а отно­шения — стрелками (рис. 40).

 

Задание 33

Придумайте различные отношения на множестве одной семьи (мама, папа, их дети — Оля, Катя, Сережа, Валера) и изобразите эти отношения с помощью графов.

В процессе игры или обучения детям постоянно приходится рассматривать элементы одного множества и устанавливать отноше­ния между ними:

• сравнивать по величине;

• подбирать одинаковые по цвету или форме;

• упорядочивать;

• делить на группы.

Очень важным считается умение ребенка определять взаимно об­ратные отношения. Например: «больше — меньше», «длиннее — ко­роче», «старше — младше» и др.

В математике изучают разнообразные отношения. Чтобы облег­чить решение этой задачи, отношения классифицируют по свой­ствам.