№ 97. Үшбұрыштың орта сызықтарынан салынған үшбұрыштың периметрі 15 дм. Берілген үшбұрыштың периметрін есептеңдер.
Берілгені: 
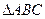үшбұрышы
орта сызықтар
Табу керек: 
Шешуі: 
Жауабы: 30 дм
Қосымша есептер.
1. Үшбұрыштың орта сызығы 5 см. Оған параллель қабырғасы 6 см бола ала ма? (Жоқ)
2. Тең бүйірлі үшбұрыштың орта сызығы 3 дм. Егер оның периметрі 16 дм болса, онда бүйір қабырғасы неге тең? (5 дм)
3. Теңбүйірлі үшбұрыштың периметрі 13 см, ал бүйір қабырғасы табанынан 2 см қысқа. Теңбүйірлі үшбұрыштың орта сызығы неге тең?
х + х + х + 2 = 
13; 3х = 11; х = 11/3
х + 2 = 17/3; 17/3: 2 = 17/6
жауабы: 17/6
4. АВС үшбұрышы – теңқабырғалы. Егер 
кесіндісі 
үшбұрышының орта сызығы және 
ге тең болса, онда берілген үшбұрыштың периметрін табыңдар.
ЕD = а/2; АВ = ВС = АС = 2ЕD; АВ = а; Р = 3а
5. Теңбүйірлі үшбұрыштың орта сызығы табанына параллель және 4 см. Үшбұрыштың периметрі 30 см болса, бүйір қабырғалары неге тең?
АС = 8 см; 30 – 8 = 22; АВ = ВС = 11 см
№98. Үшбұрыштың қабырғаларының қатынасы 4:3:5 қатынасындай. Қабырғаларының орталарын қосқанда пайда болған үшбұрыштың периметрі 3,6 дм. Берілген үшбұрыштың қабырғаларын табыңдар.
Берілгені: ΔАВС Шешуі: РΔАВС = АВ + ВС + АС
АВ: ВС:АС РΔЕҒD = АВ + ВС + АС
4:3:5 2
РΔЕҒD = 3,6 дм АВ + ВС + АС = 2*РΔЕҒD
т/к: АВ,ВС,АС -? АВ + ВС + АС = 7,2
7,2: (4+ 3+ 5) = 0,6
АВ = 4*0,6 = 2,4 (дм)
ВС = 3*0,6 = 1,8 (дм)
АС = 5*0,6 = 3 (дм)
Жауабы: 2,4 дм; 1,8 дм; 3 дм
ІV. Сабақты қорытындылау.
Оқушылардың өткен материалды еске түсіру нәтижелерін сұрақ-жауап арқылы анықтау.
1. Үшбұрыштың орта сызығы дегеніміз не?
2. Үшбұрыштың орта сызығы қалай анықталады?
3. Берілген үшбұрыш пен оның орта сызықтарынан пайда болған үшбұрыштың периметрлерінің қатынасы қандай болады?
V. Үйге тапсырма. §6. № 98 есеп, қосымша есеп № 3
VI. Бағалау. Оқушылардың білім-біліктілігін анықтап баға қою.
8-сынып.Геометрия.
Сабақ-16. мерзімі-24.10.12
Сабақтың тақырыбы: Трапецияның орта сызығы
Сабақтың мақсаты: Трапецияның орта сызығы ұғымын меңгерту
а ) Білімділік: Трапецияның орта сызығының анықтамасын біле отырып, қасиетін ұғындырып, пайдалана білуге үйрету
ә) Дамытушылық: Трапецияның орта сызығының қасиеттерін қолдану арқылы есептер шығартуға дағдыландыру
б) Тәрбиелік: Оқушыларды жылдам ойлауға, жауапкершілікті сезінуге тәрбиелеу.
Сабақтың әдісі: Түсіндірмелі – көрнекілік, ақпараттық технология
Сабақтың типі: Жаңа сабақты меңгерту
Сабақтың көрнекілігі: Үшбұрыш сызбасы, сызғыш, әр түрлі үшбұрыштар
Сабақтың барысы: І. Ұйымдастыру кезеңі. Оқушылардың сабаққа қатысуын,дайындығын тексеру.Оқушылармен амандасу.
ІІ.Өткенді пысықтау. Ой қозғау
Трапеция тақырыбы бойынша қайталау сұрақтары:
а) Трапецияның анықтамасы
ә) Трапеция түрлері
б) Теңбүйірлі трапецияның қасиеттері
Үй тапсырмасын тексеру №98
№98. Үшбұрыштың қабырғаларының қатынасы 4:3:5 қатынасындай. Қабырғаларының орталарын қосқанда пайда болған үшбұрыштың периметрі 3,6 дм. Берілген үшбұрыштың қабырғаларын табыңдар.
Берілгені: ΔАВС Шешуі: РΔАВС = АВ + ВС + АС
АВ: ВС:АС РΔЕҒD = АВ + ВС + АС
4:3:5 2
РΔЕҒD = 3,6 дм АВ + ВС + АС = 2*РΔЕҒD
т/к: АВ,ВС,АС -? АВ + ВС + АС = 7,2
7,2: (4+ 3+ 5) = 0,6
АВ = 4*0,6 = 2,4 (дм)
ВС = 3*0,6 = 1,8 (дм)
АС = 5*0,6 = 3 (дм)
Жауабы: 2,4 дм; 1,8 дм; 3 дм
ІІІ. Жаңа сабақ.
Анықтама. Трапецияның бүйір қабырғаларының отасын қосатын кесіндіні трапецияның орта сызығы деп атайды.
трапеция
орта сызығы
Теорема. Трапецияның орта сызығы табандарына параллель және табандарының қосындысының жартысына тең.
Берілгені: трапеция
орта сызығы
Дәлелдеу керек:
1. 
2. 
Дәлелдеу: 
нүктесі арқылы 
мен 
табандарына параллель түзулер жүргізсек, ал 
бүйір қырын 
нүктесінде қиып өтеді. 
болғандықтан Фалес теоремасы бойынша 
. Олай болса трапецияның орта сызығы, салуымыз бойынша 
. Демек, теореманың бірінші бөлігі дәлелденді.
Теореманың 
диагоналін жүргізсек, Фалес теоремасы бойынша О нүктесі де кесіндісінің ортасы болады. Ендеше 
-ның, 
-ның орта сызығы болады.
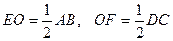. Оларды қоссақ 
, теорема дәлелденді.
1-2 мысалдарды қарастыру. Шешу үлгілері оқулықта көрсетілген.
