Приклад 1 По відрізку прямого дроту довжиною l = =80 см проходить струм силою I = 50 А. Визначити магнітну індукцію В поля, що створюється цим струмом, в точці А, яка рівновіддалена від кінців відрізка дроту і знаходиться на відстані r0 = 30 см від його середини (рис.40).
Розв’язання. Для розв’язання задачі скористаємося законом Біо-Савара-Лапласа і принципом суперпозиції магнітних полів. Закон Біо-Савара-Лапласа дозволяє визначити магнітну індукцію dB, що створюється елементом струму Idl. Зазначимо, що вектор  в точці А напрямлений за площину
в точці А напрямлений за площину

Рисунок 40 - Магнітна індукція, що створюється відрізком прямого дроту зі струмом
креслення. Принцип суперпозиції дозволяє для визначення В скористатися геометричним складанням (інтегруванням):
 , (1)
, (1)
де символ l означає, що інтегрування проводиться по всій довжині дроту.
Запишемо закон Біо-Савара-Лапласа у векторній формі
 ,
,
де  - магнітна індукція, що створюється елементом дроту довжиною dl із струмом I у точці, визначеній радіусом-вектором
- магнітна індукція, що створюється елементом дроту довжиною dl із струмом I у точці, визначеній радіусом-вектором 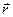 ;
;  - магнітна стала;
- магнітна стала;  – магнітна проникність середовища, в якому знаходиться дріт (в нашому випадку
– магнітна проникність середовища, в якому знаходиться дріт (в нашому випадку  = 1, оскільки середовище - повітря). Помітимо, що вектори dB від різних елементів струму співнапрямлені (рис. 40), тому вираз (1) можна переписати в скалярній формі:
= 1, оскільки середовище - повітря). Помітимо, що вектори dB від різних елементів струму співнапрямлені (рис. 40), тому вираз (1) можна переписати в скалярній формі:
 , (2)
, (2)
де
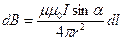 .
.
В скалярній формі закону Біо-Савара-Лапласа кут  - це кут між елементом струму
- це кут між елементом струму  і радіусом - вектором
і радіусом - вектором 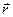 . Таким чином:
. Таким чином:
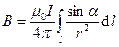 . (3)
. (3)
Перетворимо підінтегральний вираз так, щоб в ньому була тільки одна змінна - кут  . Для цього виразимо довжину елемента дроту dl через кут
. Для цього виразимо довжину елемента дроту dl через кут  :
:  (рис.40). Врахуємо також, що
(рис.40). Врахуємо також, що
 .
.
Тоді вираз (3) можна переписати у вигляді

де 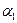 і
і 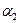 - межі інтегрування. Виконаємо інтегрування:
- межі інтегрування. Виконаємо інтегрування:
 . (4)
. (4)
Помітимо, що при симетричному розташуванні точки А відносно відрізка дроту  . З урахуванням цього формула (4) набуде вигляду
. З урахуванням цього формула (4) набуде вигляду
 . (5)
. (5)
З рис.40 видно, що
 .
.
Підставивши цей вираз у співвідношення (4), знайдемо
 .
.
Після підстановки у вираз числових значень фізичних величин отримаємо
 =26,7 10-6 Тл.
=26,7 10-6 Тл.
Напрямок вектора магнітної індукції поля, що створене прямим струмом, можна визначити за правилом свердлика (правилом правого гвинта).
Перевіримо розмірність отриманої величини (Тл):
 =
=  =
=  =
=  =
=  .
.
Тут ми скористалися визначенням магнітної індукції
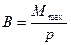
Тоді 1Тл= 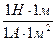 .
.
Відповідь  = 26,7×10-6 Тл.
= 26,7×10-6 Тл.
Приклад 2 По тонкому провідному кільцю радіусом R = 10 см проходить струм I = 80 А. Знайти магнітну індукцію В в точці А, рівновіддаленій від усіх точок кільця на відстань r =20 см.
Розв’язання. Для розв’язання задачі скористаємося законом Біо-Савара-Лапласа:
 , (6)
, (6)
де  - магнітна індукція поля, створеного елементом струму
- магнітна індукція поля, створеного елементом струму  в точці, що визначена радіусом-вектором
в точці, що визначена радіусом-вектором 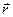 .
.
Виділимо на кільці елемент dl і від нього в точку А проведемо радіус-вектор 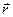 (рис.41). Вектор
(рис.41). Вектор  направимо відповідно до правила свердлика перпендикулярно до вектора
направимо відповідно до правила свердлика перпендикулярно до вектора 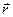 .
.

Рисунок 41 – Магнітна індукція, що створюється кільцем в точці А
Згідно з принципом суперпозиції магнітних полів магнітна індукція  в точці А визначається інтегруванням
в точці А визначається інтегруванням

де інтегрування проводиться по всіх елементах dl кільця.
Розкладемо вектор  на дві складові:
на дві складові: 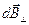 , перпендикулярну до площини кільця, і
, перпендикулярну до площини кільця, і  , паралельну площині кільця, тобто
, паралельну площині кільця, тобто
 ,
,
тоді
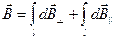
З міркувань симетрії легко помітити, що 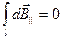 . Одночасно вектори
. Одночасно вектори 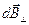 від різних елементів
від різних елементів  співнапрямлені, в результаті векторне додавання (інтегрування) можна замінити скалярним
співнапрямлені, в результаті векторне додавання (інтегрування) можна замінити скалярним
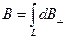 ,
,
де  , а
, а  (оскільки елемент
(оскільки елемент  перпендикулярний
перпендикулярний 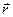 ,
, 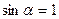 ). Таким чином:
). Таким чином:
 . (7)
. (7)
У цьому співвідношенні врахуємо, що  та проведемо скорочення
та проведемо скорочення
 . (8)
. (8)
Виразимо всі фізичні величини у (8) в одиницях СІ і проведемо обчислення
 =6,28×10-5 Тл.
=6,28×10-5 Тл.
Вектор  напрямлений по осі кільця (пунктирна стрілка на рис.41) відповідно до правила свердлика.
напрямлений по осі кільця (пунктирна стрілка на рис.41) відповідно до правила свердлика.
Перевіримо розмірність отриманої величини (Тл):
 =
=  =
=  =
=  =
=  .
.
Відповідь:  =6,28×10-5 Тл.
=6,28×10-5 Тл.
Приклад 3 Два нескінченно довгих дроти схрещені під прямим кутом (рис.42). По дротах проходять струми 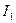 = 80 А і
= 80 А і  = 60 А. Відстань між дротами дорівнює d =10 см. Визначити магнітну індукцію
= 60 А. Відстань між дротами дорівнює d =10 см. Визначити магнітну індукцію  в точці А, однаково віддаленій від обох дротів.
в точці А, однаково віддаленій від обох дротів.


Рисунок 42 – Магнітна індукція, що створена двома схрещеними дротами
Розв’язання. Відповідно до принципу суперпозиції магнітних полів магнітна індукція  поля, створеного струмами
поля, створеного струмами 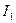 і
і  в точці А, визначається векторною сумою полів, створених кожним струмом окремо
в точці А, визначається векторною сумою полів, створених кожним струмом окремо 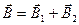 .
.
Помітимо, що вектори  і
і 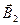 взаємно перпендикулярні (їх напрями знаходяться за правилом свердлика і зображені в двох проекціях на рис.42). Тоді модуль вектора
взаємно перпендикулярні (їх напрями знаходяться за правилом свердлика і зображені в двох проекціях на рис.42). Тоді модуль вектора  можна визначити за теоремою Піфагора:
можна визначити за теоремою Піфагора:
 , (9)
, (9)
де  і
і 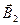 визначаються за формулами розрахунку магнітної індукції для нескінченно довгого прямолінійного дроту із струмом:
визначаються за формулами розрахунку магнітної індукції для нескінченно довгого прямолінійного дроту із струмом:
 і
і  (10)
(10)
У нашому випадку  . Тоді, підставивши співвідношення (10) у (9), одержимо
. Тоді, підставивши співвідношення (10) у (9), одержимо
 . (11)
. (11)
Проведемо обчислення:
 =
=  Тл.
Тл.
Перевіримо розмірність отриманої величини (Тл):
 =
=  =
=  =
=  =
=  .
.
Відповідь:  =
=  Тл.
Тл.
Приклад 4 Стрижень довжиною  заряджений рівномірно розподіленим зарядом з лінійною густиною
заряджений рівномірно розподіленим зарядом з лінійною густиною  . Стрижень обертається з частотою
. Стрижень обертається з частотою 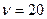 с-1 відносно осі, що перпендикулярна до нього і проходить через його кінець (рис. 43). Визначити магнітний момент
с-1 відносно осі, що перпендикулярна до нього і проходить через його кінець (рис. 43). Визначити магнітний момент  ,обумовлений обертанням стрижня.
,обумовлений обертанням стрижня.
 |
Рисунок 43 – Стрижень з розподіленим зарядом, що обертається навколо осі ОО`
Розв’язання. Виділимо на стрижні елемент довжиною  (рис.43), на даному елементі знаходиться заряд
(рис.43), на даному елементі знаходиться заряд  . При обертанні стрижня відносно осі ОО` цей заряд обумовлює струм
. При обертанні стрижня відносно осі ОО` цей заряд обумовлює струм
 , (12)
, (12)
де  - період обертання стрижня;
- період обертання стрижня;  - частота обертання.
- частота обертання.
Магнітний момент, що створюється струмом 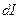 ,за визначенням дорівнює
,за визначенням дорівнює
 , (13)
, (13)
де площу контуру S можна знайти із співвідношення
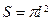 . (14)
. (14)
Підставимо співвідношення (12) і (14) в (13), тоді знайдемо
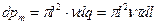 .
.
Проінтегруємо даний вираз за довжиною стрижня 
 . (15)
. (15)
Підставивши числові значення фізичних величин у співвідношення (15), отримаємо відповідь

Перевіримо розмірність отриманої величини ( ):
):
 =
= 
Відповідь:  .
.
 Приклад 5 Диск радіусом
Приклад 5 Диск радіусом  несе рівномірно розподілений по поверхні заряд
несе рівномірно розподілений по поверхні заряд  (рис.44). Визначити магнітний момент
(рис.44). Визначити магнітний момент  , обумовлений обертанням диска відносно осі, що проходить через його центр і перпендикулярна до площини диска. Кутова швидкість обертання диска
, обумовлений обертанням диска відносно осі, що проходить через його центр і перпендикулярна до площини диска. Кутова швидкість обертання диска  .
.
Рисунок 44 – Диск з розподіленим зарядом, що обертається навколо осі ОО`
Розв’язання. Для знаходження магнітного моменту диска зобразимо його у вигляді сукупності тонких кілець шириною  (рис. 44).
(рис. 44).
Виділимо на диску елемент площі  із зарядом
із зарядом 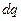
 . (16)
. (16)
При обертанні диска відбувається переміщення електричних зарядів. Сила струму, що відповідає даному руху, визначається співвідношенням
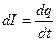 . (17)
. (17)
З урахуванням рівняння (16) отримаємо
 . (18)
. (18)
Магнітний момент даного струму визначається співвідношенням
 , (19)
, (19)
де площа контуру дорівнює  .
.
Після підстановки виразів (17) і (18) в (19) та урахування того, що за визначенням  , отримаємо
, отримаємо
 . (20)
. (20)
Повний магнітний момент диска буде дорівнювати сумі (інтегралу) векторів  . Оскільки ці вектори мають однаковий напрям, векторну суму можна замінити скалярною. Після інтегрування (20) одержимо
. Оскільки ці вектори мають однаковий напрям, векторну суму можна замінити скалярною. Після інтегрування (20) одержимо
 (21)
(21)
Підставивши числові значень фізичних величин, знайдемо відповідь
 .
.
Перевіримо розмірність отриманої величини ( ):
):
 =
=  .
.
Відповідь: 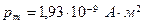 .
.
Приклад 6 Квадратна дротяна рамка із стороною а = =5 см і опором R = 10 мОм знаходиться в однорідному магнітному полі (В = 40 мТл). Нормаль до площини рамки складає кут  з лініями магнітної індукції. Визначити заряд Q, який пройде по рамці, якщо магнітне поле вимкнути.
з лініями магнітної індукції. Визначити заряд Q, який пройде по рамці, якщо магнітне поле вимкнути.
Розв’язання. При відключенні магнітного поля відбудеться зміна магнітного потоку, що пронизує рамку. Внаслідок цього в рамці виникне ЕРС індукції, яку можна визначити, скориставшись основним законом електромагнітної індукції
 . (22)
. (22)
ЕРС індукції, що виникла, викличе в рамці індукційний струм, миттєве значення якого можна визначити, скориставшись законом Ома для повного кола
 , (23)
, (23)
де R - опір рамки.
Тоді, прирівнявши співвідношення (22) та (23), одержимо
 .
.
Оскільки миттєве значення сили індукційного струму  , той цей вираз можна переписати у вигляді
, той цей вираз можна переписати у вигляді
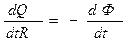 ,
,
звідси
 . (24)
. (24)
Проінтегрувавши співвідношення (24), знайдемо
 ,
,
або
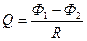 .
.
З урахуванням того, що при вимкненому полі (кінцевий стан) 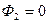 , остання рівність перепишеться у вигляді
, остання рівність перепишеться у вигляді
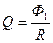 . (25)
. (25)
Знайдемо магнітний потік  . За визначенням магнітного потоку маємо
. За визначенням магнітного потоку маємо
 ,
,
де  - площа рамки.
- площа рамки.
В нашому випадку (рамка є квадратом)  .
.
Тоді

 . (26)
. (26)
Підставивши співвідношення (26) в (25), отримаємо
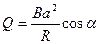 .
.
Проведемо обчислення
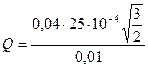 = 8,67×10-3 Кл.
= 8,67×10-3 Кл.
Переконаємося в тому, що права частина цієї рівності дає одиницю заряду (Кл)
 .
.
Відповідь: 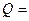 8,67×мКл.
8,67×мКл.
Приклад 7 Тонкий мідний дріт масою  зігнутий у вигляді квадрата, кінці якого замкнені. Квадрат розміщений у однорідному магнітному полі
зігнутий у вигляді квадрата, кінці якого замкнені. Квадрат розміщений у однорідному магнітному полі  так, що його площина перпендикулярна до ліній поля. Визначити заряд DQ, який пройде по провіднику, якщо квадрат, потягнувши його за протилежні вершини, витягнути у лінію.
так, що його площина перпендикулярна до ліній поля. Визначити заряд DQ, який пройде по провіднику, якщо квадрат, потягнувши його за протилежні вершини, витягнути у лінію.
Розв’язання. Заряд, що проходить через контур внаслідок зміни його форми, визначається виразом
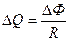 , (27)
, (27)
де  – зміна магнітного потоку, що пронизує контур;
– зміна магнітного потоку, що пронизує контур;  – опір дроту, з якого виготовлений контур.
– опір дроту, з якого виготовлений контур.
Зміна магнітного потоку дорівнює
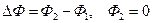 ,
,
де 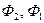 - магнітні потоки, що пронизують контур до і після його деформації.
- магнітні потоки, що пронизують контур до і після його деформації.
Магнітний потік, що пронизує контур в початковий момент, знайдемо із співвідношення
 , (28)
, (28)
де  - кут між нормаллю до рамки і напрямком вектора магнітної індукції;
- кут між нормаллю до рамки і напрямком вектора магнітної індукції;  - площа контуру.
- площа контуру.
Підставивши вираз (28) в (27), отримаємо
 . (29)
. (29)
Площа контуру дорівнює 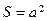 .
.
Опір контуру знайдемо із співвідношення
 , (30)
, (30)
де 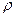 - питомий опір міді;
- питомий опір міді;  – площа перерізу дроту,
– площа перерізу дроту,  – довжина дроту.
– довжина дроту.
За умовою задачі
 . (31)
. (31)
Підставивши співвідношення (30) і (31) в (29), отримаємо
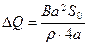 . (32)
. (32)
Площу поперечного перерізу дроту знайдемо із виразу  , де
, де  – густина міді (
– густина міді ( ). Врахуємо, що
). Врахуємо, що  , звідси
, звідси
 . (33)
. (33)
Підставивши вираз (33) в (32), отримаємо
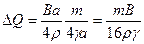 . (34)
. (34)
Після підставлення числових значень величин у співвідношення (34) отримаємо остаточну відповідь
 .
.
Перевіримо розмірність отриманої величини ( ):
):
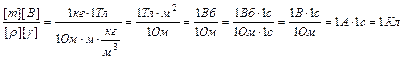 .
.
Відповідь: 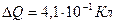 .
.
Приклад 8 Плоский квадратний контур (рис.45) із стороною а = 10 см, по якому тече струм I =100 А, вільно встановився в однорідному магнітному полі (В = 1 Тл). Визначити роботу А, що здійснюється зовнішніми силами при повороті контуру відносно осі, що проходить через середину його протилежних сторін, на кут  . При повороті контуру сила струму, що підтримується в ньому, є незмінною.
. При повороті контуру сила струму, що підтримується в ньому, є незмінною.

Рисунок 45 – Плоский контур у магнітному полі
Розв’язання. Як відомо, на контур із струмом у магнітному полі діє момент сили (рис.45)
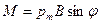 , (35)
, (35)
де  - магнітний момент контуру; В - магнітна індукція;
- магнітний момент контуру; В - магнітна індукція;  - кут між векторами
- кут між векторами  (який направлений по нормалі до контуру) і
(який направлений по нормалі до контуру) і  .
.
За умовою задачі в початковому положенні контур вільно встановився в магнітному полі. При цьому момент сили дорівнює нулю (M = 0), а, отже,  = 0, тобто вектори
= 0, тобто вектори  і
і  співнапрямлені. Якщо зовнішні сили виведуть контур з положення рівноваги, то момент сил, що виникне (див. рис.45), прагнутиме повернути контур у початкове положення. Проти цього моменту і здійснюється робота зовнішніми силами. Оскільки момент сил є змінним (залежить від кута повороту
співнапрямлені. Якщо зовнішні сили виведуть контур з положення рівноваги, то момент сил, що виникне (див. рис.45), прагнутиме повернути контур у початкове положення. Проти цього моменту і здійснюється робота зовнішніми силами. Оскільки момент сил є змінним (залежить від кута повороту  ), то для розрахунку роботи застосуємо формулу роботи в диференціальній формі
), то для розрахунку роботи застосуємо формулу роботи в диференціальній формі  . Враховуючи співвідношення (35), одержимо
. Враховуючи співвідношення (35), одержимо
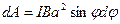 . (36)
. (36)
Взявши інтеграл від виразу (36), знайдемо роботу при повороті рамки на кінцевий кут:
 . (37)
. (37)
Робота при повороті на кут  дорівнює
дорівнює
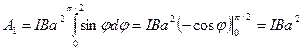 . (38)
. (38)
Виразимо числові значення величин в одиницях СІ і підставимо в (38):
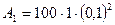 = 1 Дж.
= 1 Дж.
Перевіримо розмірність отриманої величини ( ):
):
 .
.
Відповідь:  1 Дж.
1 Дж.
Приклад 9 Соленоїд має 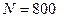 витків. Переріз його сердечника із немагнітного матеріалу становить
витків. Переріз його сердечника із немагнітного матеріалу становить 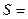 10 см2. По обмотці проходить струм, який створює поле з індукцією
10 см2. По обмотці проходить струм, який створює поле з індукцією 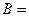 8 мТл. Визначити середнє значення ЕРС
8 мТл. Визначити середнє значення ЕРС  самоіндукції, яка виникає на затискачах соленоїда, якщо сила струму зменшується практично до нуля за час
самоіндукції, яка виникає на затискачах соленоїда, якщо сила струму зменшується практично до нуля за час  0,8 мс.
0,8 мс.
Розв’язання. ЕРС індукції визначається законом електромагнітної індукції
 , (39)
, (39)
де  - потокозчеплення.
- потокозчеплення.
Магнітний потік, що створюється соленоїдом, дорівнює
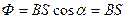 , (40)
, (40)
де  - кут між нормаллю до площини витків та вектором магнітної індукції. За умовою задачі
- кут між нормаллю до площини витків та вектором магнітної індукції. За умовою задачі  ,
,  .
.
Потокозчеплення соленоїда визначається виразом
 . (41)
. (41)
Підставивши співвідношення (40) в (41), отримаємо
 . (42)
. (42)
Оскільки  0, то
0, то  .
.
З урахуванням даного виразу (39) набуде вигляду
 . (43)
. (43)
Підставивши числові значення фізичних величин у вираз (43), отримаємо
 .
.
Переконаємося в тому, що права частина цієї рівності дає одиницю напруги (В)
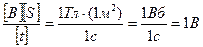 .
.
Відповідь:  .
.
Приклад 10 Протон, що пройшов прискорювальну різницю потенціалів U = 600 В, влетів в однорідне магнітне поле з індукцією В = 0,3 Тл і почав рухатися по колу (рис. 46). Обчислити радіус R кола.

Рисунок 46 - Рух зарядженої частинки у магнітному полі
Розв’язання. Рух зарядженої частинки в однорідному магнітному полі буде відбуватися по колу (рис. 46) тільки у тому випадку, коли частинка влетить в магнітне поле перпендикулярно до ліній магнітної індукції,  .
.
Оскільки сила Лоренца перпендикулярна до вектора  , то вона надасть частинці (протону) нормального прискорення
, то вона надасть частинці (протону) нормального прискорення  . Згідно з другим законом Ньютона
. Згідно з другим законом Ньютона
 , (44)
, (44)
де m - маса протона.
На рис.46 траєкторія протона суміщена з площиною креслення і вказаний (довільно) напрям вектора  . Силу Лоренца спрямуємо перпендикулярно до вектора
. Силу Лоренца спрямуємо перпендикулярно до вектора  до центра кола (вектори
до центра кола (вектори 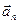 і
і  співнапрямлені). Використовуючи правило лівої руки, визначимо напрям магнітних силових ліній (напрям вектора
співнапрямлені). Використовуючи правило лівої руки, визначимо напрям магнітних силових ліній (напрям вектора  ).
).
Перепишемо вираз (44) у скалярній формі (в проекції на напрямок радіуса):
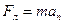 (45)
(45)
Модуль сили Лоренца дорівнює  . У нашому випадку
. У нашому випадку  і
і 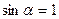 , тоді
, тоді  . Оскільки нормальне прискорення
. Оскільки нормальне прискорення  , то співвідношення (45) набуде вигляду
, то співвідношення (45) набуде вигляду
 .
.
Звідси знайдемо радіус кола:
 . (46)
. (46)
Помітивши, що  , де
, де  - імпульс протона, цей вираз можна записати у вигляді
- імпульс протона, цей вираз можна записати у вигляді
 . (47)
. (47)
Імпульс протона знайдемо, скориставшись зв’язком між роботою сил електричного поля і зміною кінетичної енергії протона, тобто  , або
, або
 ,
,
де  - прискорювальна різниця потенціалів (або прискорювальна напруга U);
- прискорювальна різниця потенціалів (або прискорювальна напруга U);  - початкова і кінцева кінетичні енергії протона.
- початкова і кінцева кінетичні енергії протона.
Нехтуючи початковою кінетичною енергією протона  і виразивши кінетичну енергію
і виразивши кінетичну енергію  через імпульс р, отримаємо
через імпульс р, отримаємо
 .
.
Знайдемо з цього співвідношення імпульс  і підставимо його у формулу (46):
і підставимо його у формулу (46):
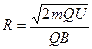
або
 . (48)
. (48)
Підставивши у цей вираз числові значення фізичних величин, проведемо обчислення  :
:
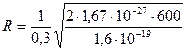 = 11,8 мм.
= 11,8 мм.
Переконаємося в тому, що права частина рівності дає одиницю довжини (м):
 =
= 
 .
.
Відповідь:  = 11,8 10-3 м.
= 11,8 10-3 м.
Приклад 11 Електрон рухається в однорідному магнітному полі (B = 10мТл) по гвинтовій лінії, радіус якої дорівнює R =1 см і крок h = 6 см (рис.47). Визначити період Т обертання електрона і його швидкість 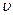 .
.

Рисунок 47 – Рух зарядженої частинки у магнітному полі
Розв’язання. Електрон рухатиметься по гвинтовій лінії, якщо він влітає в однорідне магнітне поле під деяким кутом ( ) до ліній магнітної індукції. Розкладемо, як це показано на рис.47, швидкість
) до ліній магнітної індукції. Розкладемо, як це показано на рис.47, швидкість 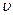 електрона на дві складові: паралельну вектору
електрона на дві складові: паралельну вектору  (
( ) і перпендикулярну йому (
) і перпендикулярну йому ( ). Швидкість
). Швидкість  в магнітному полі не змінюється і забезпечує переміщення електрона вздовж силової лінії. Швидкість
в магнітному полі не змінюється і забезпечує переміщення електрона вздовж силової лінії. Швидкість  в результаті дії сили Лоренца буде змінюватися тільки за напрямом (
в результаті дії сили Лоренца буде змінюватися тільки за напрямом ( ) (за відсутності паралельної складової (
) (за відсутності паралельної складової ( = 0) рух електрона відбувався б по колу в площині, перпендикулярній до магнітних силових ліній). Таким чином, електрон братиме участь одночасно в двох рухах: рівномірному переміщенні із швидкістю
= 0) рух електрона відбувався б по колу в площині, перпендикулярній до магнітних силових ліній). Таким чином, електрон братиме участь одночасно в двох рухах: рівномірному переміщенні із швидкістю  і рівномірному русі по колу із швидкістю
і рівномірному русі по колу із швидкістю  .
.
Період обертання електрона пов’язаний з перпендикулярною складовою швидкості співвідношенням
 . (49)
. (49)
Знайдемо  . Для цього скористаємося тим, що сила Лоренца надає електрону нормального прискорення
. Для цього скористаємося тим, що сила Лоренца надає електрону нормального прискорення  . Згідно з другим законом Ньютона можна написати
. Згідно з другим законом Ньютона можна написати
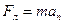
або
 , (50)
, (50)
де  .
.
З цього співвідношення знайдемо  та підставимо у (49), після простих перетворень отримаємо
та підставимо у (49), після простих перетворень отримаємо
 . (51)
. (51)
Модуль швидкості 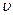 , як це показано на рис.47, можна виразити через
, як це показано на рис.47, можна виразити через  :
:
 .
.
Із співвідношення (50) виразимо перпендикулярну складову швидкості:
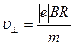 ..
..
Паралельну складову швидкості  знайдемо з наступних міркувань. За час, що дорівнює періоду обертання Т, електрон пройде вздовж силової лінії відстань, що дорівнює кроку гвинтової лінії, тобто
знайдемо з наступних міркувань. За час, що дорівнює періоду обертання Т, електрон пройде вздовж силової лінії відстань, що дорівнює кроку гвинтової лінії, тобто  , звідки
, звідки
 .
.
Підставивши замість Т праву частину співвідношення (49), отримаємо
 .
.
Таким чином, модуль швидкості електрона дорівнює
 . (52)
. (52)
Проведемо обчислення періоду обертання та швидкості електрона:
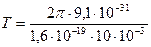
 = 3,57 нс.
= 3,57 нс.

 .
.
Переконаємося в тому, що права частина рівності (51) дає одиницю часу (с), а співвідношення (52) - одиницю швидкості (м/с).
 .
.
Оскільки R і h мають однакову одиницю вимірювання - метр (м), у квадратних дужках ми поставимо тільки одну з величин (наприклад, R):

Відповідь: 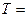 3,57 10-9 с,
3,57 10-9 с, 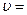
 .
.
Приклад 12 Альфа-частинка пройшла прискорювальну різницю потенціалів U = 104 В і влетіла в схрещені під прямим кутом електричне (E =10 кВ/м) і магнітне (В = 0,1 Тл) поля. Знайти відношення заряду альфа-частинки до її маси, якщо, рухаючись перпендикулярно до обох полів, частинка не відхиляється від прямолінійної траєкторії (рис.48).
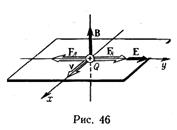
Рисунок 48 – Рух зарядженої частинки у схрещених магнітному та електричному полях
Розв’язання. Для того щоб знайти відношення заряду Q альфа-частинки до її маси m, скористаємося зв’язком між роботою сил електричного поля і зміною кінетичної енергії частинки:
 .
.
Звідки
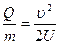 . (53)
. (53)
Швидкість 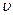 альфа-частинки знайдемо з наступних міркувань. У схрещених електричному і магнітному полях на заряджену частинку, що рухається, діють дві сили:
альфа-частинки знайдемо з наступних міркувань. У схрещених електричному і магнітному полях на заряджену частинку, що рухається, діють дві сили:
а) сила Лоренца  , спрямована перпендикулярно до швидкості
, спрямована перпендикулярно до швидкості  і вектора магнітної індукції
і вектора магнітної індукції  ;
;
б) кулонівська сила  , співнапрямлена з вектором напруженості
, співнапрямлена з вектором напруженості  електростатичного поля (Q >0).
електростатичного поля (Q >0).
На рис.48 спрямуємо вектор магнітної індукції  вздовж осі Oz, швидкість
вздовж осі Oz, швидкість 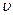 - в позитивному напрямі осі Ох, тоді
- в позитивному напрямі осі Ох, тоді  і
і  будуть спрямовані так, як показано на рисунку.
будуть спрямовані так, як показано на рисунку.
Альфа-частинка буде рухатися прямолінійно, якщо геометрична сума сил  =
=  буде дорівнювати нулю. В проекції на вісь Оу отримаємо таку рівність (при цьому враховано, що
буде дорівнювати нулю. В проекції на вісь Оу отримаємо таку рівність (при цьому враховано, що  і
і 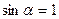 ):
):
 .
.
Звідки
 . (54)
. (54)
Підставивши цей вираз у формулу (53), отримаємо
 . (55)
. (55)
Проведемо обчислення:
 мКл/кг.
мКл/кг.
Переконаємося в тому, що права частина рівності дає одиницю питомого заряду (Кл/кг):
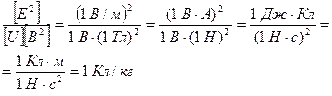
Відповідь:  мКл/кг.
мКл/кг.
Приклад 13 Частинка масою m = 0,01 кг здійснює гармонічні коливання з періодом T = 2 с. Повна енергія частинки, що коливається, становить E = 0,1 мДж. Визначити амплітуду А коливань і найбільше значення сили  що діє на частинку.
що діє на частинку.
Розв’язання. Для визначення амплітуди коливань скористаємося виразом повної енергії частинки:
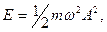
де  Звідси амплітуда
Звідси амплітуда
 . (56)
. (56)
Оскільки частинка здійснює гармонічні коливання, то сила, що діє на неї, є квазіпружною і, отже, може бути виражена співвідношенням F=-kx, де k - коефіцієнт квазіпружної сили; x - зміщення точки, що коливається. Максимальною сила буде при максимальному зміщенні 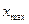 , що дорівнює амплітуді:
, що дорівнює амплітуді:
 . (57)
. (57)
Коефіцієнт k виразимо через період коливань:
 (58)
(58)
Підставивши вирази (56) і (58) в (57) і провівши спрощення, отримаємо

Проведемо обчислення:
 мм,
мм,

Відповідь: 

Приклад 14 Складаються два коливання однакового напрямку, що описуються рівняннями  де
де  = 3 cм
= 3 cм 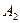 = 2 см
= 2 см  = 1/6 с
= 1/6 с 
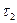 = 1/3 с, Т =2 с. Побудувати векторну діаграму складання цих коливань і написати рівняння результуючого коливання.
= 1/3 с, Т =2 с. Побудувати векторну діаграму складання цих коливань і написати рівняння результуючого коливання.
Розв’язання. Для побудови векторної діаграми складання двох коливань одного напрямку треба зафіксувати який-небудь момент часу. Як правило, векторну діаграму будують для моменту часу t = 0. Перетворивши обидва рівняння до канонічної форми  , отримаємо
, отримаємо
 (59)
(59)
Звідси бачимо, що обидва гармонічні коливання, які складаються, мають однакову циклічну частоту  .
.






