От переводчика
Автор этой книги И.Лакатос, профессор Лондонского экономического училища, является, одним из видных деятелей в области математической логики – части математики, особенно быстро развивающейся в наше время. На первой странице английского издания Лакатоса есть посвящение: «К 75‑летию Георга Полья и 60‑летию Карла Поппера». Первый из этих двух ученых хорошо известен в нашей математической литературе книгой «Задачи и теоремы из анализа», составленной им совместно с Г.Сеге и переведенной в 30‑е годы на русский язык профессором Б.А.Райковым.
Книга И.Лакатоса является как бы продолжением другой книги Г.Полья – «Математика и допустимые рассуждения» (Polya G. (1954). Mathematics and plausible reasoning, I – II. London). Разобрав вопросы, касающиеся возникновения догадки и ее проверки, Полья в своей книге остановился на фазе доказательства; исследованию этой фазы и посвящена предлагаемая вниманию читателей книга Лакатоса. Конечно, автор преследовал и другие цели, о которых он говорит во введении, но широкому кругу читателей интересно не столько введение, имеющее существенное значение для специалистов, сколько основной текст, понимание которого доступно даже школьникам старших классов. Берется простая стереометрическая теорема, касающаяся соотношения между числами сторон, вершин и граней многогранника, и разбираются ее возможные доказательства. Изложение ведется в двух планах: один из них – это рассказ о разговорах, возникших среди учеников в связи с обсуждением правильности рассматриваемых доказательств, другой план составляют подстрочные примечания, дающие действительную историю этих доказательств и вскрывающие ошибки, которые делались при этом математиками XIX в диалоги учеников – это по существу и есть наглядное отражение этой истории. Таким образом, читатель вводится в рабочую мастерскую математиков, знакомится с созданием доказательств, а не только с окончательными результатами, излагаемыми в учебниках.
Карл Поппер – один из видных представителей неопозитивизма, примыкавший в 30‑е годы к «венскому кружку» (Карнап, Рейхенбах и др.). В послевоенные годы он осел в Англии. Поппер если и эволюционировал, то в сторону скептицизма, а в вопросах обоснования математики – в сторону конвенционализма, т.е. утверждения чисто условного характера научных положений. Влияние Поппера на И.Лакатоса несомненно. Однако наш читатель не сделает тех скептических выводов, к которым пытается подвести его автор, а найдет в этом насыщенном историческим материалом произведении немало ярких доказательств того, что математика в познании действительности идет по тому же диалектическому пути, что и другие науки.
Нужно отметить особый характер ссылок: цитируемые книги обозначены именем автора и временем издания; по этим данным в библиографии, помещенной в конце книги, читатель может найти точное название источника.
Написанная легко и остроумно, книга И.Лакатоса доставила переводчику много удовольствия во время работы над ней. Он желает, чтобы такое же удовольствие испытали и ее читатели.
8 сентября 1966 г.
Профессор И.Н.Веселовский
Введение
В истории мысли часто случается, что при появлении нового мощного метода быстро выдвигается на авансцену изучение задач, которые этим методом могут быть решены, в то время как все остальное игнорируется, даже забывается, а изучением его пренебрегают.
Именно это как будто произошло в нашем столетии в области философии математики в результате стремительного развития метаматематики.
Предмет метаматематики состоит в такой абстракции математики, когда математические теории заменяются формальными системами, доказательства – некоторыми последовательностями хорошо известных формул, определения – «сокращенными выражениями», которые «теоретически необязательны, но зато типографически удобны»[1].
Такая абстракция была придумана Гильбертом, чтобы получить мощную технику исследования задач методологии математики. Вместе с тем имеются задачи, которые выпадают из рамок метаматематической абстракции. В их числе находятся все задачи, относящиеся к «содержательной» математике и ее развитию, и все задачи, касающиеся ситуационной[2] логики и решения математических задач. Школу математической философии, которая стремится отождествить математику с ее метаматематической абстракцией (а философию математики – с метаматематикой), я буду называть «формалистской» школой. Одна из самых отчетливых характеристик формалистской позиции находится у Карнапа[3]. Карнап требует, чтобы (а) философия была заменена логикой науки…, но (в) «логика науки представляет не что иное, как логический синтаксис языка науки»…, (с) «метаматематика же является синтаксисом математического языка» (Carnap R. (1937). The logical syntax of language. N.Y. London, стр. XIII и 9). Итак, философию математики следует заменить метаматематикой.
Формализм отделяет историю математики от философии математики, так как согласно формалистскому пониманию математики, собственно говоря, истории математики не существует. Любой формалист целиком будет согласен с замечанием Рассела, высказанным «романтически», но сделанным вполне серьезно, что «Законы мысли» Буля (Boole, 1854) были «первой книгой когда-либо написанной по математике»[4]. Формализм отрицает статус математики для большей части того, что обычно понималось как входящее в математику, и ничего не может сказать об ее «развитии». Ни один из «творческих» периодов и вряд ли один из «критических» периодов математических теорий может быть допущен в формалистическое небо, где математические теории пребывают как серафимы, очищенные от всех пятен земной недостоверности. Однако формалисты обычно оставляют открытым небольшой черный ход для падших ангелов; если для каких-нибудь «смесей математики и чего-то другого» окажется возможным построить формальные системы, «которые в некотором смысле включают их», то они могут быть тогда допущены. При таких условиях Ньютону пришлось прождать четыре века, пока Пеано, Рассел и Куайн (Quine) помогли ему влезть на небо, формализовав его исчисление бесконечно малых. Дирак оказался более счастливым: Шварц спас его душу еще при его жизни. Может быть, мы должны упомянуть здесь парадоксальное затруднение метаматематика: по формалистским или даже по дедуктивистским стандартам он не является честным математиком. Дьёдонне говорит об «абсолютной необходимости для каждого математика, который заботится об интеллектуальной честности (разрядка моя. – Авт.), представлять свои рассуждения в аксиоматической форме» (Dieudonne J. (1939). Les methodes axiomatiques modernes et les fondements des mathematiques. – стр. 225).
При современном господстве формализма невольно впадаешь в искушение перефразировать Канта: история математики, лишившись руководства философии, сделалась слепой, тогда как философия математики, повернувшись спиной к наиболее интригующим событиям истории математики, сделалась пустой.
«Формализм» представляет крепость логической позитивистской философии. Если следовать логическому позитивизму, то утверждение имеет смысл только, если оно является «тавтологическим» или эмпирическим. Так как содержательная математика не является ни «тавтологической», ни эмпирической, то она должна быть бессмысленной, она – чистый вздор[5]. Догматы логического позитивизма гибельны для истории и философии математики.
Целью этих статей является подход к некоторым проблемам методологии математики. Я употребляю слово «методология» в смысле, близком к «эвристике»[6] Полья и Бернайса и к «логике открытия» или «ситуационной логике» Поппера[7]. Недавняя экспроприация термина «методология математики» для использования в качестве синонима «метаматематики» имеет несомненно формалистский привкус. Это показывает, что в формалистской философии математики нет настоящего места для методологии как логики открытия[8]. Если верить формалистам, то математика будет тождественна формализованной математике. Но что можно открыть в формализованной теории? Два ряда вещей. Во-первых, можно открыть решение задач, которые машина Тюринга при подходящей программе может решить за конечное время (как, например, будет ли некоторое предложенное доказательство действительно доказательством или нет?). Ни один математик не заинтересован в том, чтобы следить за этим скучным механическим «методом», предписываемым процедурами такого решения. Во-вторых, можно найти решения задач вроде: будет ли теоремой или нет некоторая формула теории, в которой не установлена возможность окончательного решения, где можно руководствоваться только «методом» неуправляемой интуиции и удачи.
Так вот, для живой математики непригодна эта мрачная альтернатива машинного рационализма и иррационального отгадыванпя вслепую[9]. Исследование неформальной математики дает творческим математикам богатую ситуационную логику, которая не будет ни механической, ни иррациональной, но которая никак не может получить признания, тем более поощрения формалистской философии.
История математики и логика математического открытия, т.е. филогенез и онтогенез[10] математической мысли, не могут быть развиты без критицизма и окончательного отказа от формализма.
Но формалистская философия математики имеет очень глубокие корни. Она представляет последнее звено в длинной цепи догматистских философий математики. Ведь уже более двух тысяч лет идет спор между догматиками и скептиками. Догматики утверждают, что силой нашего человеческого интеллекта и чувств, или только одних чувств, мы можем достичь истины и узнать, что мы ее достигли. Скептики, с другой стороны, или утверждают, что мы совершенно не можем достичь истины (разве только при помощи мистического эксперимента), или что если даже сможем достичь ее, то не можем знать, что мы ее достигли. В этом большом споре, в котором время от времени аргументы осовременивались, математика была гордой крепостью догматизма. Всякий раз, когда математический догматизм попадал в «кризис», какая-нибудь новая версия снова придавала ему подлинную строгость и настоящие основы, восстанавливая образ авторитарной, непогрешимой, неопровержимой математики – «единственной науки, которую Бог захотел дать человечеству» (Hobbes T. (1651). Leviathan, or the matter, form and power of a Commonwealth, Ecclesiastical and Civil. London). Большая часть скептиков примирилась с неприступностью этой крепости догматистской теории познания[11]. Бросить этому вызов – давно уже стало необходимым.
Цель этого этюда и есть этот вызов математическому формализму, но это не прямой вызов основным положениям математического догматизма. Наша скромная цель состоит в установлении положения, что неформальная квазиэмпирическая математика не развивается как монотонное возрастание количества несомненно доказанных теорем, но только через непрерывное улучшение догадок при помощи размышления и критики, при помощи логики доказательств и опровержений. Поскольку, однако, метаматематика представляет парадигму неформальной квазиэмпирической математики и в настоящее время находится в быстром росте, то эта статья тем самым бросает вызов со временному математическому догматизму. Исследователь недавней истории метаматематики найдет на его собственном поле описанные здесь образцы.
Диалогическая форма должна отразить диалектику рассказа; она должна содержать своего рода рационально реконструированную или «дистиллированную» историю. Реальная история будет звучать в подстрочных примечаниях, большая часть которых поэтому должна быть рассматриваема как органическая часть статьи.
Задачи и догадка
Диалог происходит в воображаемой классной комнате. Класс заинтересовался задачей: существует ли соотношение между числом V вершин, числом E ребер и, наконец, числом F граней многогранника – в частности, правильного многогранника – аналогично тривиальному соотношению между числами вершин и сторон многоугольников, а именно: что существует столько же сторон, сколько и вершин: 
? Последнее соотношение позволяет классифицировать многоугольники по числу сторон (или вершин): треугольники, четырехугольники, пятиугольники и т.д. Аналогичное соотношение поможет классификации многогранников.
После большого количества испытаний и ошибок класс замечает, что для всех правильных многогранников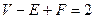 
[12].
Кто-то высказывает догадку, что это может быть приложимым к любому многограннику. Другие пытаются оспорить эту догадку, испытать ее многими разными способами – она выдерживает хорошо. Этот результат подкрепляет догадку и наводит на мысль, что она может быть доказана. В этот момент – после стадий постановки задачи и догадок – мы входим в классную комнату[13]. Учитель как раз готовится дать доказательство.
Доказательство
Учитель. На нашем последнем уроке мы пришли к догадке относительно многогранников, а именно: что для всех многогранников 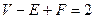, где V – число вершин, E – число ребер и F – число граней. Мы испытали ее различными способами. Но мы пока еще не доказали ее. Может быть, кто-нибудь нашел доказательство?
Ученик Сигма. Я со своей стороны должен сознаться, что пока еще не придумал строгого доказательства этой теоремы… Однако истинность ее была установлена в очень многих случаях, и не может быть сомнения, что она справедлива для любого тела. Таким образом, это предложение, по-видимому, доказано вполне удовлетворительно[14]. Но если у вас есть доказательство, то, пожалуйста, дайте его.
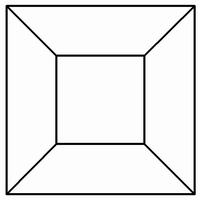
Рис. 1
Рис. 2
Учитель. Действительно, я его имею. Оно состоит в следующем мысленном эксперименте. Первый шаг. Вообразим, что многогранник будет полым с поверхностью из резины. Если мы вырежем одну из его граней, то всю остальную поверхность мы можем, не разрезая, растянуть на плоской доске. Грани и ребра будут деформироваться, ребра могут стать криволинейными, но V, E и F не изменятся, так что если и только если 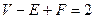для первоначального многогранника, то 
для этой плоской сети – вспомните, что мы одну грань удалили. (На рис. 1 показана такая сеть для куба.) Второй шаг. Теперь мы стриангулируем нашу карту – она действительно выглядит как географическая карта. Проведем (может быть, криволинейные) диагонали в тех (может быть, криволинейных) многоугольниках, которые еще не являются (может быть, криволинейными) треугольниками. Проведя каждую диагональ, мы увеличиваем и E и F на единицу, так что сумма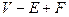 
не изменится (рис. 2).
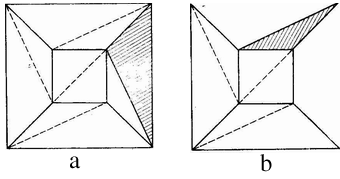
Рис. 3
Третий шаг. Теперь будем вынимать из триангулированной сети треугольники один за другим. Вынимая треугольник, мы или вынимаем ребро, причем исчезают одна грань и одно ребро (рис. 3, а), или вынимаем два ребра и вершину; тогда исчезают одна грань, два ребра и одна вершина (рис. 3, б). Таким образом, если до выемки треугольника, то оно останется таким же и после выемки. В конце этой процедуры мы получаем один треугольник. Для него является справедливым. Таким образом, мы доказали нашу догадку[15].
Ученик Дельта. Вы должны назвать это теперь теоремой. Теперь здесь уже нет ничего из области догадок[16].
Ученик Альфа. Не знаю. Я вижу, что этот эксперимент можно выполнить с кубом или с тетраэдром, но как я могу знать, что его можно произвести с любым многогранником. Кстати, уверены ли вы, сэр, что всякий многогранник после устранения одной грани может быть развернут плоско на доске? У меня есть сомнения относительно вашего первого шага.
Ученик Бета. Уверены ли вы, что при триангулировании карты вы всегда получите новую грань для любого нового ребра? У меня есть сомнения относительно вашего второго шага.
Ученик Гамма. Уверены ли вы, что когда вы будете откидывать треугольники один за другим, то получатся только две альтернативы – исчезновение одного ребра или же двух ребер и одной вершины? Уверены ли вы также, что в конце процесса останетесь только с одним треугольником? У меня есть сомнения относительно вашего третьего шага[17].
Учитель. Конечно, я не уверен.
Альфа. Но ведь это еще хуже, чем раньше. Вместо одной догадки, мы теперь имеем по меньшей мере три! И вы называете это «доказательством»!
Учитель. Я допускаю, что традиционное название «доказательство» для этого мысленного эксперимента, пожалуй, не совсем подходит. Я не думаю, что этот эксперимент устанавливает истинность догадки.
Дельта. Ну а что же он тогда делает? Что же, по-вашему, доказывает математическое доказательство?
Учитель. Это тонкий вопрос, на который мы попытаемся ответить позже. До тех пор я предлагаю сохранить освященный временем технический термин «доказательство» для мысленного эксперимента, или квазиэксперимента, который предлагает разложение первоначальной догадки на вспомогательные догадки пли леммы, таким образом впутывая ее, может быть, в совершенно далекую область знания. Например, наше «доказательство» в первоначальную догадку – о кристаллах, или, скажем, о твердых телах – включило теорию резиновых листов. Декарт или Эйлер, отцы первоначальной догадки, наверняка ни о чем подобном не думали[18].
Критика доказательства при помощи контрапримеров, являющихся локальными, но не глобальными
Учитель. Подсказанное доказательством разложение догадки открывает новые горизонты для проб. Это разложение более широким фронтом развертывает догадку, так что наш дух критики получает большее количество целей. Мы теперь вместо одной имеем по меньшей мере три возможности для контрапримеров.
Гамма. Я уже выразил мое несогласие с вашей третьей леммой (а именно, что при вынимании треугольников из сети, получившейся после растягивания и последующей триангуляции, мы имеем только две возможности: мы убираем или только одно ребро, или же два ребра с вершиной). Я подозреваю, что при удалении треугольника могут появиться и другие возможности.
Учитель. Подозрение – это еще не критика.
Гамма. А контрапример будет критикой?
Учитель. Конечно. Догадкам нет дела до несогласий или подозрений; но они не могут игнорировать контрапримеры.
Тета (в сторону). Догадки, очевидно, сильно отличаются от тех, кто их представляет.
Гамма. Я предлагаю очень простой контрапример. Возьмем триангуляционную сеть, которая получилась после проведения на кубе двух первых операций (см. рис. 2). Теперь, если я удалю треугольник изнутри этой сети, как можно вынуть кусок из головоломки, то я вынимаю только один треугольник без удаления каких-нибудь ребер или вершин. Таким образом, третья лемма неверна – и не только в случае куба, но для всех многогранников, кроме тетраэдра, для которого в плоской сети всё треугольники будут граничными. Таким образом, ваше доказательство доказывает теорему Эйлера для тетраэдра. Но ведь мы уже и так знали, что для тетраэдра 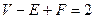, так зачем же это доказывать?
Учитель. Вы правы. Но заметьте, что куб, который представляет контрапример для третьей леммы, не будет контрапримером для основной догадки, так как для куба 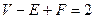. Вы показали, что аргументация доказательства имеет недостаток, но это не значит, что наша догадка ложна.
Альфа. Так, вы теперь снимете свое доказательство?
Учитель. Нет. Критика не всегда будет необходимо разрушением. Я просто исправлю мое доказательство, чтобы оно устояло против этой критики.
Гамма. Как?
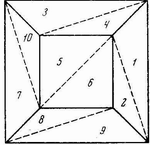
Рис. 4
Учитель. Прежде чем показать «как», давайте введем такую терминологию. Локальным контрапримером я буду называть пример, который отвергает лемму (не отвергая необходимо основную догадку), а глобальным контрапримером я назову пример, отвергающий саму догадку. Таким образом, ваш контрапример будет локальным, но не глобальным. Локальный, но не глобальный контра-пример представляет критику только доказательства, но не догадки.
Гамма. Значит, догадка может быть верной, но ваше доказательство ее не доказывает.
Учитель. Но я легко могу переработать, улучшить доказательство, заменив неверную лемму слегка исправленной, которую ваш контрапример не сможет опровергнуть. Я не буду спорить, что при вынимании любого треугольника получаются только две упомянутые возможности, но скажу только, что на каждой стадии процесса вынимания одного из граничных треугольников может встретиться одна из упомянутых возможностей. Возвращаясь к моему мысленному эксперименту, я должен только в описании моего третьего шага прибавить одно слово, а именно, что «теперь из триангулированной сети мы отнимаем один за другим граничные треугольники». Вы согласитесь, что для приведения в порядок доказательства понадобилось только небольшое замечание?[19]
Гамма. Не думаю, чтобы ваше замечание было таким пустяковым; оно, конечно, очень остроумно. Чтобы выяснить это, я покажу, что оно неверно. Возьмем опять плоскую сеть для куба и отнимем восемь из десяти треугольников в последовательности, указанной на рис. 4. При вынимании восьмого треугольника, который, конечно, будет тогда граничным, мы отняли два ребра и ни одной вершины, а это изменит 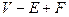на 1. И мы остались с двумя отдельными треугольниками 9 и 10.
Учитель. Ну, я мог бы спасти лицо, сказав, что под граничным треугольником я подразумевал такой, вынимание которого не нарушает связности сети. Но интеллектуальная честность препятствует мне скрыто изменять мои положения словами, начинающимися с «я думал»; поэтому я считаю, что вторую версию операции вынимания треугольников я должен заменить третьей, а именно, что вынимаются треугольники один за другим таким образом, чтобы 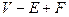не изменялось.
Каппа. Охотно соглашусь, что соответствующая такой операции лемма будет истинной: конечно, если мы вынимаем треугольники один за другим, так, чтобы 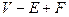не изменялось, то 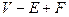не будет изменяться.
Учитель. Нет. Лемма заключается в том, что треугольники в нашей сети могут быть перенумерованы так, что при вынимании их в правильной последовательности 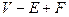не будет изменяться, пока мы не достигнем последнего треугольника.
Каппа. Но как же построить эту правильную последовательность, если она вообще существует?[20] Ваш первоначальный мысленный эксперимент давал инструкцию: вынимайте треугольники в любом порядке. А теперь вы говорите, что мы должны следовать некоторому определенному порядку, но не говорите, какой это порядок и существует ли он в действительности. Таким образом, ваш мысленный эксперимент разваливается. Вы исправили анализ доказательства, т.е. список лемм, но мысленный эксперимент, который вы назвали – «доказательством», исчез.
Ро. Исчез только третий шаг.
Каппа. Кроме того, улучшили ли вы лемму? Ваши первые две версии по крайней мере до их опровержения казались тривиально простыми, а ваша длинноватая заплатанная версия даже не кажется очевидной. Можете ли вы верить, что она избежит опровержения?
Учитель. «Очевидные» или даже «тривиально простые» предложения обычно скоро отвергаются: софистические, неочевидные предположения, созревшие после критицизма, могут оказаться истинными.
Омега. А что случится, если и ваши «софистические предположения» окажутся ложными и мы не сможем заменить их неложными? Или если вам не удастся улучшить локальными заплатами ваши аргументы? При помощи замены отвергнутой леммы вам удалось справиться с локальным контрапримером, не бывшим глобальным. А что если в следующий раз вам это не удастся?
Учитель. Вопрос хорош – поставим его завтра в повестку дня.
