При отображении X в Y каждый элемент множества X соответствует одному и только одному элементу из Y. На элементы множества Y ограничений не накладывается. Может случиться, что некоторые элементы множества Y не являются образами ни одного элемента множества X, другие являются образами точно одного элемента множества X, третьи – нескольких или даже бесконечного множества элементов множества X.
Определение. Если каждый элемент множества Y является образом хотя бы одного элемента из X, то такое отображение называют сюръекцией или отображением множества X на множество Y.
На рисунке 12 приведен пример графа такого отображения.
 |
Рис. 12
Заметим, что в множестве Y пришлось взять «меньше» элементов, чем в X. Рассмотрим теперь случай, когда в Y «больше» элементов, чем в X. В этом случае мы получим отображение множества X в множество Y.
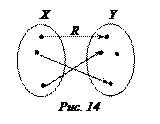
Определение. Если каждый элемент множества Y является образом не более одного элемента из X, отображение называют инъекцией.
На рисунках 13 и 14 приведены примеры графов таких отображений.
Возьмем теперь в X и Y «поровну» элементов. Построим графы отображений.
Определение. Если каждый элемент множества Y является образом точно одного элемента из X, отображение называют биекцией или взаимно однозначным отображением (соответствием).
Примеры графов таких отображений приведены на рисунках 15 и 16.
 |  |
П р и м е р. Пусть X – множество пальто в гардеробе, a Y – множество крючков в этом гардеробе. Поставим в соответствие каждому пальто крючок, на котором оно висит.
Если каждое пальто висит на крючке (а не лежит, скажем, на полу), то это соответствие является отображением X в Y. Это отображение – инъекция, если ни на одном крючке не висит более одного пальто (но могут быть свободные крючки), отображение – сюръекция, если все крючки заняты (но на некоторых крючках могут висеть несколько пальто). Наконец, это отображение – биекция (взаимно однозначно), если на каждом крючке висит одно и только одно пальто.
С биекцией связано понятие обратного отображения. Если соответствие R – биекция, обратное соответствие R -1 тоже биекция, сопоставляющая с каждым элементом из Y точно один элемент из X так, что если xRy, то yR -1 x. Чтобы из графа отображения R получить граф обратного отображения R -1, достаточно повернуть все стрелки в противоположную сторону.
Эквивалентные множества
Определение. Если существует (хотя бы одно) биективное отображение между множествами X и Y, то говорят, что множество X эквивалентно множеству Y.
Обозначают: Х ~ Y.
Покажем, что отношение эквивалентности множеств обладает свойствами рефлексивности, симметричности и транзитивности. То есть докажем следующие 3 утверждения:
1) для любого множества X имеем Х ~ Х;
2) для любых двух множеств X и Y, если X ~ Y, то Y ~ X;
3) для любых трех множеств X, Y, Z, если X ~ Y и Y ~ Z, то X ~ Z.
Чтобы доказать первое утверждение, достаточно поставить в соответствие каждому элементу х Î Х тот же самый элемент х. Такое соответствие называется тождественным отображением.
Докажем теперь второе утверждение. Отношение X ~ Y означает, что существует биективное отображение между элементами этих множеств. Рассмотрим обратное отображение между множествами Y и X, оно тоже будет биективным. Значит, Y ~ X.
Наконец, докажем утверждение 3. Действительно, отношение
Х ~ Y означает, что существует биективное отображение R: X ® Y, а отношение Y ~ Z означает, что существует отображение Q: Y ® Z. Построим отображение F: X ® Z следующим образом: с каждым элементом х Î Х сопоставим элемент z Î Z так, что если у = R (x), то z = Q (y). Это означает, что F (x) = Q (R (x)). Отображение F называется суперпозицией отображения R и Q, обозначается также F = Q 
R. Совершенно очевидно, что F – биективное отображение. Следовательно, X ~ Z.
Поскольку отношение Х ~ Y является эквивалентностью, совокупность всех множеств разбивается на классы эквивалентных друг другу множеств. Два конечных множества попадут в один класс, когда они имеют одинаковое число элементов. Это позволяет определить натуральное число как общее свойство, которым обладает класс эквивалентных друг другу конечных множеств.
