Периодические (повторяющиеся) волны

Самые важные волновые явления связаны не с одиночными волновыми импульсами а с регулярно повторяющимися последовательностямиодиночных волн. Эти повторяющиеся,или периодические волны подчиняются тем же законам, что и одиночные волновые импульсы, так что единственное, что нам нужно добавить, — это терминологиюих описания. Рис. 7-5 иллюстрирует эту терминологию.

Длина волны, для обозначения которой обычно используют строчную греческую букву 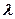(“лямбда”), — это кратчайшее расстояние в среде, на котором полностью воспроизводится картина волны, то есть повторяется её pattern [45].

Амплитуд а выражает величину максимального смещения, произведенного волной.

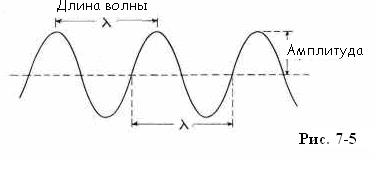Еще одна величина необходима для описания периодических волн: ведь так как волна перемещается, то каждая точка на её пути участвует в движении, которое полностью повторяет себя при прохождении каждой длины волны через эту точку. Количество повторений этого движения, которое происходит за одну секунду, называют частотой, которую обычно обозначают греческой буквой 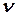(“ню”). Частоту измеряют в “ циклах в секунду” [46]. Единицу измерения частоты (1/c ) также называют герц (Гц), в честь исследователя радиоволн Г. Р. Герца [47]. Величина, обратная частоте: 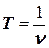, называется периодом волны и измеряется в секундах.)

Иногда вместо длины волны удобно использовать волновое число, 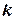, — число волн, укладывающихся на одном метре длины. Эта величина обратна длине волны: .

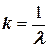Конечно, длина волны и её частота (период) тесно связаны между собой, так как волна распространяется с постоянной скоростью. Например, если частота волны равна 5 Гц, то есть каждую секунду происходит 5 полных колебательных циклов, а длина волны равна 4 м, то за секунду волна должна переместиться на 20 м (20 м/с). Эта зависимость может быть выражена итоговой формулой:

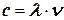или 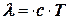(7.1),

где 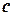– условное обозначение для скорости волны. Это не физический закон в обычном смысле, а скорее соотношение, которое прямо следует из определений длины волны и частоты.

Гладкая волна, показанная на рис. 7-5, известна как синусоидальная волна, поскольку в её математическом описании используется тригонометрическая функция синус. Звуковая волна такой формы, слышна как чистый музыкальный тон, высота которого определяется частотой волны. Синусоидальная световая волна дает чистый спектральный цвет. Волны могут иметь практически любую вообразимую форму. Когда эта форма достоверно повторяется на протяжении многих длин волн (периодов), то можно использовать принцип суперпозиции для того, чтобы представить сложную по форме волну как комбинацию синусоидальных волн различной длины волны и амплитуды.

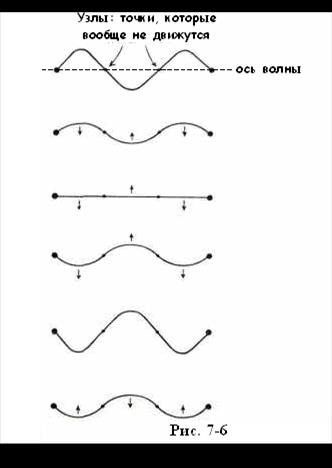
Когда волна ограничена неподвижными границами, такими, например, как концы струны, мы получаем великолепную модель стоячей волны, пример которой показан на рисунке 7-6. Все струнные музыкальные инструменты производят свои звуки подобным образом. Волновое движение в стоячейволне происходит перпендикулярно оси волны. В бегущей же волне волновое движение происходит вдоль оси волны.)[48]

Стоячая волна может существовать на струне, только если закрепленные концы струны будут оставаться неподвижными. А так как профиль волны должен пересекать ось волны через каждую половину длины волны, то единственными волнами, способными “выжить” на струне, будут те, у которых эта половина 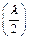составляет ровно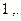 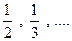часть от длины струны. Случай для трёх половин длин волны и показан на рис. 7-6. Точки, которые вообще не движутся, называют узлами стоячей волны.

Так как более коротким длинам волн соответствуют более высокие частоты, то волну с профилем, соответствующим одной половине длины волны, называют основным тоном, более короткие волны называют гармониками или обертонами. Принцип суперпозиции позволяет многим гармоникам сосуществовать на струне в одно и то же время. Это именно то, что придает музыкальным инструментам их характерный звук, так как чисто синусоидальная волна создает, довольно скучный, механический звук[49].

Радиопередатчик создает стоячую электрическую волну в своей антенне. Лазер генерирует стоячую световую волну, ограниченную с обоих концов зеркалами, и содержит внутри себя устройства для “накачки” волны энергией. Когда мы доберемся до квантовой теории, мы встретимся с ещё более интересным типом стоячих волн.