Пока мы рассмотрели только одномерные (1-d) волны, то есть волны, распространяющиесяв струне, в линейной среде. Не менее знакомы нам двумерные волны в форме длинных горных хребтов и впадин на двумерной поверхности воды. Следующий шаг при обсуждении волн нам предстоит сделать в пространство двух (2-d) и трех (3-d) измерений. Опять-таки никакие новые физические принципы не будут использоваться; задача состоит просто в описании волновых процессов.
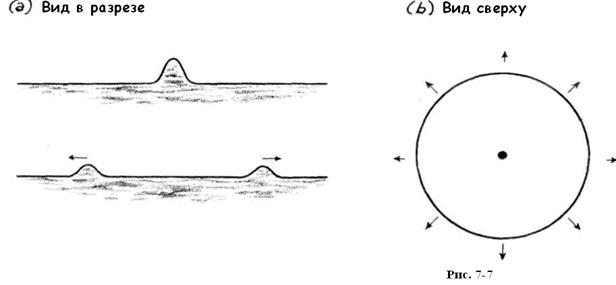
Мы начнем обсуждение, вернувшись к той простой ситуации, с которой начиналась эта глава — одиночный волновой импульс. Однако теперь это будет не возмущение на струне, а всплеск на поверхности водоема. Всплеск оседает под своим собственным весом, а смежные с ним области, испытывая повышенное давление, подымаются, начиная распространение волны. Этот процесс “в разрезе” изображен на рис. 7-7(a). Дальнейшая логика рассмотрения ситуации точно такая же, что уже была использована при изучении эффектов, возникающих после резкого удара по центральной части струны. Но на сей раз волна может перемещаться во всех направлениях. Не имея причин предпочесть одно какое-то направление другому, волна распространяется во всехнаправлениях. Результат — знакомый всем расширяющийся круг ряби на поверхности тихого водоема, см. рис. 7-7 (b).
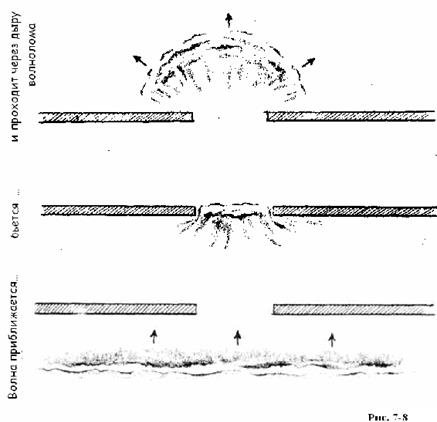
 Хорошо знакомы нам и плоские волны на поверхности воды — те волны, гребни которых образуют длинные, иногда практически параллельные, линии на поверхности воды. Это те самые волны, которые периодически накатывают на берег. Интересной особенностью волн такого типа является тот способ, которым они преодолевают препятст-вия — например, дыры в непрерывной стене волнолома. Рисунок 7-8 иллюстрирует этот процесс. Если размер отверстия сравним с длиной волны, то каждая последовательная волна создает в пределах отверстия всплеск, который, как и на рис. 7-7, служит источником круглой ряби в акватории порта. В результате между волнорезом и берегом возникают концентрические, “ кольцевые ” волны.
Хорошо знакомы нам и плоские волны на поверхности воды — те волны, гребни которых образуют длинные, иногда практически параллельные, линии на поверхности воды. Это те самые волны, которые периодически накатывают на берег. Интересной особенностью волн такого типа является тот способ, которым они преодолевают препятст-вия — например, дыры в непрерывной стене волнолома. Рисунок 7-8 иллюстрирует этот процесс. Если размер отверстия сравним с длиной волны, то каждая последовательная волна создает в пределах отверстия всплеск, который, как и на рис. 7-7, служит источником круглой ряби в акватории порта. В результате между волнорезом и берегом возникают концентрические, “ кольцевые ” волны.
Это явление известно как дифракция волн. Если же ширина дыры в волноломе будет намного больше, чем длина волны, то этого не случится — прошедшие через препятствие волны сохранят свою плоскую форму, разве что на краях волны возникнут слабые искажения
Подобно волнам на поверхности воды, существуют и трехмерные волны (3-d –волны). Здесь самый знакомый пример — это звуковые волны. Гребень звуковой волны — это область сгущения [50]молекул воздуха. Рисунок, аналогичный рис. 7-7 для трехмерного случая представлял бы расширяющуюся волну в форме сферы.
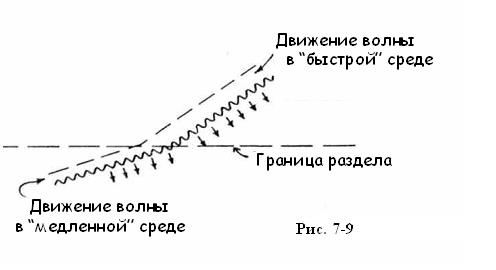 Все волны обладают свойством преломления. Это эффект, который возникает когда волна проходит через границу двух сред, и попадает в среду, в которой она движется более медленно[51]. Особенно наглядно выглядит этот эффект в случае плоских волн (см. рис. 7-9). Та часть плоской волны, которая оказалась в новой, “медленной”, среде движется в ней с меньшей скоростью. Но поскольку эта часть волны неизбежно остается связанной с волной в “быстрой” среде, её фронт (пунктирная линия в нижней части рис.7-9) должен изломиться, то есть приблизиться к границе раздела двух сред, как это и показано на рис. 7-9.
Все волны обладают свойством преломления. Это эффект, который возникает когда волна проходит через границу двух сред, и попадает в среду, в которой она движется более медленно[51]. Особенно наглядно выглядит этот эффект в случае плоских волн (см. рис. 7-9). Та часть плоской волны, которая оказалась в новой, “медленной”, среде движется в ней с меньшей скоростью. Но поскольку эта часть волны неизбежно остается связанной с волной в “быстрой” среде, её фронт (пунктирная линия в нижней части рис.7-9) должен изломиться, то есть приблизиться к границе раздела двух сред, как это и показано на рис. 7-9.
Если же изменение скорости распространения волны происходит не скачком, а постепенно, то и поворот фронта волны будет происходить тоже плавно. Это, кстати, объясняет причину того, почему волны прибоя, независимо от того, как они двигались в открытой воде, почти всегда параллельны береговой линии. Дело в том, что с уменьшением толщины водного слоя скорость волн на его поверхности уменьшается, поэтому у берега, где волны попадают в область мелководья, они замедляются. Постепенный поворот их фронта и делает волны практически параллельными береговой линии.






